Positional Embedding

位置编码的内容难以一文穷尽，这篇文章主要是让自己了解基本内容和重要技术

positional embedding? position embedding? positional encoding?

Overview

Attention无法获取位置信息，需要显式加入位置编码
位置编码分为绝对位置编码与相对位置编码

• 绝对位置编码比较简单，直接对位置进行编码，并不能直接表示位置间关系(即相对信息)，一般加入到对应位置的向量中 $x_k=x_k+p_k$ 使用绝对位置编码的例子有：BERT(作为参数学习)，Transformer(Sinusoidal)
• 相对位置编码用相对位置向量替换绝对位置向量，灵活性更大，更适合于自然语言任务(依赖于相对位置)，实现一般比较复杂。 使用相对位置编码的有XLNET, T5, DeBERTa
  在苏神看来，位置编码的目标是使用绝对编码的方式实现相对编码

一开始位置编码只加在embedding层，后来发展为每个attention层计算一次
相对位置编码在注意力计算阶段加入，一开始加入到$qk$计算中和$v$中，后来只加到$q,k$计算中

Sinusoidal

来自 1706.03762

$$\{\begin{array}{l}{p}_{k,2i}=\sin \left(k/10000^{2i/d}\right)\\ p_{k,2i+1}=\cos \left(k/10000^{2i/d}\right)\end{array}$$

其中$k$是位置，$d$是向量维度，$2i,2i+1$ 表示向量中偶数或奇数分量

RoPE

盛极一时的位置编码
来自苏神 Transformer升级之路：2、博采众长的旋转式位置编码 - 科学空间|Scientific Spaces
以下是阅读博客的笔记

目的

使用绝对位置编码的方式实现相对位置编码，就是要实现为$q,k$加入绝对位置信息

$${\tilde{q}}_m=f(q,m),{\tilde{k}}_n=f(k,n)$$

$f(\cdot ,m)$ 是加入绝对位置信息的操作
在注意力计算(内积)的过程中，出现相对位置信息

$$⟨f(q,m),f(k,n)⟩=g(q,k,m-n)$$

求解

合理设$f(q,0)=q$ 和 $f(k,0)=k$

从二维开始，借助复数求解。

首先，复数与内积的联系在于，二维向量能够转化为一个复数，复数相乘 $q$与$k^{\ast }$(*表示共轭)的实部就是二维向量$q,k$的内积

$$\mathrm{Re}[f(q,m)f^{\ast }(k,n)]=g(q,k,m-n)$$

$\mathrm{Re}[]$ 表示取实部

使用复数的指数形式

$$f(q,m)=R_f(q,m)e^{\mathrm{i}{\Theta }_f(q,m)}$$ $$f(k,n)=R_f(k,n)e^{\mathrm{i}{\Theta }_f(k,n)}$$ $$g(q,k,m-n)=R_g(q,k,m-n)e^{i{\Theta }_g(q,k,m-n)}$$

$\Theta (q)$ 是幅角，$R_g{\Theta }_g$在满足等式的情况下可以任意选择

Addition

关于复数的指数形式

复数的指数形式也叫极坐标形式或欧拉公式表示法
欧拉公式
$e^{i\theta }=cos\theta +isin\theta$
假设复数为
$z=a+bi$
指数形式为
$z=r{e}^{i\theta }$
其中 $r$ 为 复数的模，$\theta$ 是复数的幅角(相位角)(与实轴之间的夹角)
$\theta =atan2(b,a)$

代入复数的指数形式得到方程组

$$R_f(\mathbf{q},m)R_f(\mathbf{k},n)=R_g(\mathbf{q},\mathbf{k},m-n)$$ $${\Theta }_f(\mathbf{q},m)-{\Theta }_f(\mathbf{k},n)={\Theta }_g(\mathbf{q},\mathbf{k},m-n)$$

对于第一个方程，代入$m=n$ ，根据初始条件得到

$$R_f(\mathbf{q},m)R_f(\mathbf{k},m)=R_g(\mathbf{q},\mathbf{k},0)=R_f(\mathbf{q},0)R_f(\mathbf{k},0)=\Vert \mathbf{q}\Vert \Vert \mathbf{k}\Vert$$

因为我们只需要一个解，所以设$R_f(\mathbf{q},m)=||q||$，$R_f(\mathbf{k},m)=||k||$

对于第二个方程，同样代入$m=n$得到

$${\Theta }_f(q,m)-{\Theta }_f(k,m)={\Theta }_g(q,k,0)={\Theta }_f(q,0)-{\Theta }_f(k,0)=\Theta (q)-\Theta (k)$$

进一步可以得到

$${\Theta }_f(q,m)-\Theta (q)={\Theta }_f(k,m)-\Theta (k)$$

可以看出，${\Theta }_f(q,m)-\Theta (q)$的结果与$q/k$无关，只与位置$m$有关。设其为函数$\phi (m)$
即

$${\Theta }_f(q,m)-\Theta (q)=\phi (m)$$

代入$n=m-1$到第二个方程，可以得到

$${\Theta }_f(\mathbf{q},m)-{\Theta }_f(\mathbf{k},m-1)={\Theta }_g(\mathbf{q},\mathbf{k},1)$$

构造$\phi (m)$可得

$${\Theta }_f(\mathbf{q},m)-{\Theta }_f(q)-{\Theta }_f(\mathbf{k},m-1)+{\Theta }_f(k)={\Theta }_g(\mathbf{q},\mathbf{k},1)-{\Theta }_f(q)+{\Theta }_f(k)$$

即

$$\phi (m)-\phi (m-1)={\Theta }_g(q,k,1)+\Theta (k)-\Theta (q)$$

得到$\{\phi (m)\}$ 是等差数列，设右部为$\theta$，得到通解为 $\phi (m)=m\theta$
则${\Theta }_f(q,m)$ 得解

$${\Theta }_f(q,m)=\Theta (q)+\phi (m)$$

则在二维的情况下，解为

$$f(q,m)=R_f(q,m)e^{\mathrm{i}{\Theta }_f(q,m)}=\Vert q\Vert e^{\mathrm{i}(\Theta (q)+m\theta )}=q{e}^{\mathrm{i}m\theta }$$

这里是拆分了指数得到复数$q$ 乘以 $e^{im\theta }$

在复数中，这样的形式(复数乘法)相当于对复数逆时针旋转$\theta$度，称旋转位置编码(Rotary Position Embedding RoPE)

具体形式

$f(q,m)$可以写成矩阵形式

$$f(q,m)=\left(\begin{array}{cc}\cos m\theta & -\sin m\theta \\ \sin m\theta & \cos m\theta \end{array}\right)\left(\begin{array}{c}{q}_0\\ q_1\end{array}\right)$$

内积满足线性叠加性，任意偶数维的向量(Embedding 基本都是偶数维度的)，都可以使用RoPE

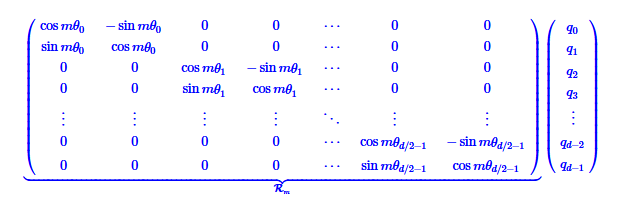
所以实际编码时，只需要为q和k都乘以RoPE矩阵就可以得到RoPE编码

$$({\mathcal{R}}_m\mathbf{q}{)}^{\top }({\mathcal{R}}_n\mathbf{k})={\mathbf{q}}^{\top }{\mathcal{R}}_m^{\top }{\mathcal{R}}_n\mathbf{k}={\mathbf{q}}^{\top }{\mathcal{R}}_{n-m}\mathbf{k}$$

矩阵是稀疏的，所以直接这样相乘会浪费算力，苏神推荐

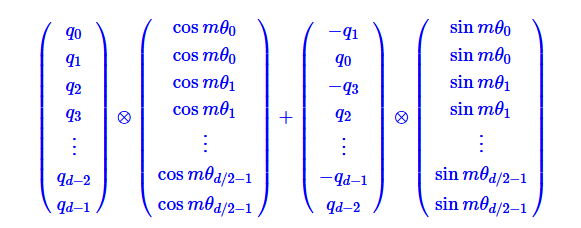
$\otimes$ 是按位相乘

${\theta }_i$怎么选择

RoPE选择了与Sinusoidal位置编码一致的 ${\theta }_i=10000^{-2i/d}$
已验证这样选择的${\theta }_i$具有远程衰减性(随着相对距离增大，注意力分数减小)

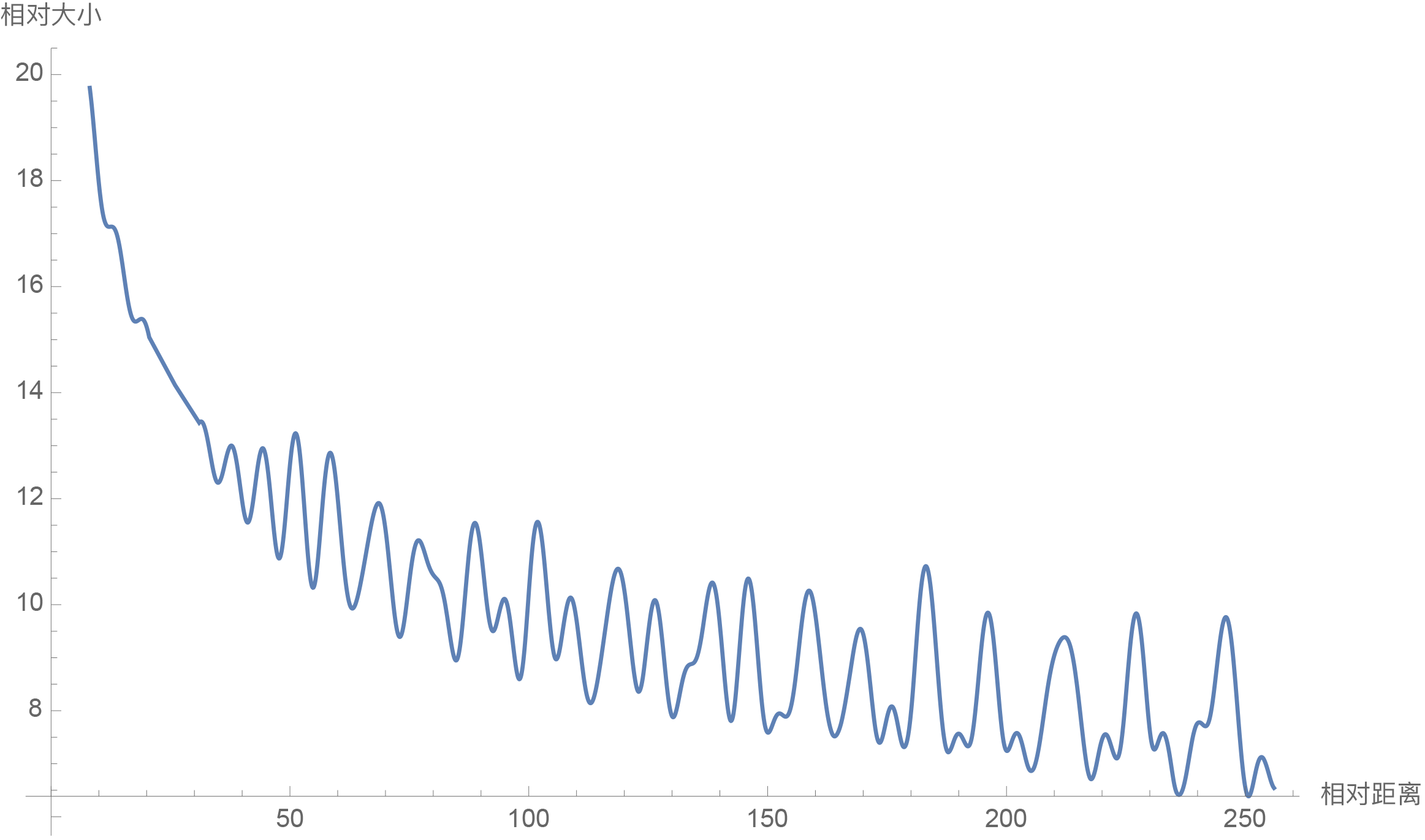
图像与具体验证均来自苏神博客 Transformer升级之路：2、博采众长的旋转式位置编码 - 科学空间|Scientific Spaces

代码实现与讨论

在研究代码实现时产生的不一定正确的讨论

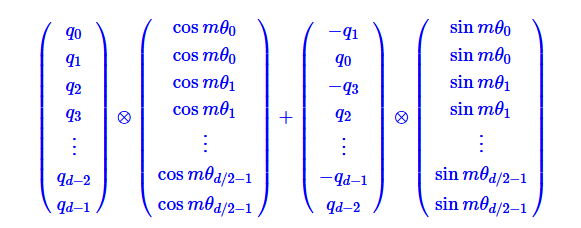
这样的实现方式产生了一种可能性：分组有没有可能可以不按顺序(非相邻)
如果按照矩阵相乘来实现的话，应该就是相邻两个维度为一组，不使用矩阵避免了稀疏矩阵浪费算力，但是这样的计算要求以2为步数找出各个分组。
即(Mesh Transformer)

def rotate_every_two(x):
    x1 = x[:, :, ::2]
    x2 = x[:, :, 1::2]
 
    x = jnp.stack((-x2, x1), axis=-1)
 
    return rearrange(x, "... d j -> ... (d j)")

粗浅的计算机知识，这样的方法会产生多次缓存未命中，应该会在IO上耗时，代码虽然复合原文但是比较不优雅

而有另一个优雅的实现(Llama3, GPT-NeoX)

import torch
 
 
class Rotary(torch.nn.Module):
    def __init__(self, dim, base=10000):
        super().__init__()
        inv_freq = 1.0 / (base ** (torch.arange(0, dim, 2).float() / dim))
        self.register_buffer("inv_freq", inv_freq)
        self.seq_len_cached = None
        self.cos_cached = None
        self.sin_cached = None
 
    def forward(self, x, seq_dim=1):
        seq_len = x.shape[seq_dim]
        if seq_len != self.seq_len_cached:
            self.seq_len_cached = seq_len
            t = torch.arange(x.shape[seq_dim], device=x.device).type_as(self.inv_freq)
            freqs = torch.einsum("i,j->ij", t, self.inv_freq)
            emb = torch.cat((freqs, freqs), dim=-1).to(x.device)
            self.cos_cached = emb.cos()[:, None, None, :]
            self.sin_cached = emb.sin()[:, None, None, :]
        return self.cos_cached, self.sin_cached
 
 
# rotary pos emb helpers:
 
def rotate_half(x):
    x1, x2 = x[..., : x.shape[-1] // 2], x[..., x.shape[-1] // 2 :]
    return torch.cat(
        (-x2, x1), dim=x1.ndim - 1
    )  # dim=-1 triggers a bug in torch < 1.8.0
 
 
@torch.jit.script
def apply_rotary_pos_emb(q, k, cos, sin):
    return (q * cos) + (rotate_half(q) * sin), (k * cos) + (rotate_half(k) * sin)

在rotate_half 中，竟然直接将前一半与后一半作为一组((0, 1) -> (0, d//2-1))

但这样可行吗？

代码中首先是对$m{\theta }_i$进行了特殊处理，

inv_freq = 1.0 / (base ** (torch.arange(0, dim, 2).float() / dim))
freqs = torch.einsum("i,j->ij", t, self.inv_freq)
emb = torch.cat((freqs, freqs), dim=-1).to(x.device)

如果原本的$m\theta$是2, 0.2, 0.02, 0.002，则实现了

(2, 2, 0.2, 0.2, 0.02, 0.02, 0.002, 0.002) # 原本
-> (2, 0.2, 0.02, 0.002, 2, 0.2, 0.02, 0.002) # 现在

这样的处理使得新的分组，每一组进行的旋转计算是一致的
即每一组形如0, d//2-1 都进行了同一个$m\theta$ 的旋转

那是否意味着只要保持每一组旋转相同就可以，无所谓相邻？
原博客中，相邻似乎不是必要条件。只要所有的$q,k$，都进行了相同形式的旋转位置编码，就能实现RoPE。又或者说，Embedding中的每一个维度是独立的，不存在相关性。一个Embedding是一个高维的向量，则任一维度放在向量的任何地方都应该是没有区别的，只需要所有向量都保持一致就行。则向量内的顺序无关紧要，只需要两个维度的元素构成一个复数，进行对应的旋转就满足RoPE的数学要求?

这么算一定和原来结果不一样，但是仍然编码了位置信息。

References

• LLM：旋转位置编码（RoPE）的通俗理解
• Transformer升级之路：2、博采众长的旋转式位置编码 - 科学空间|Scientific Spaces
• Transformer升级之路：1、Sinusoidal位置编码追根溯源 - 科学空间|Scientific Spaces
• Rotary Embeddings: A Relative Revolution | EleutherAI Blog
• 2104.09864v4
• transformers/src/transformers/models/llama/modeling_llama.py at main · huggingface/transformers · GitHub