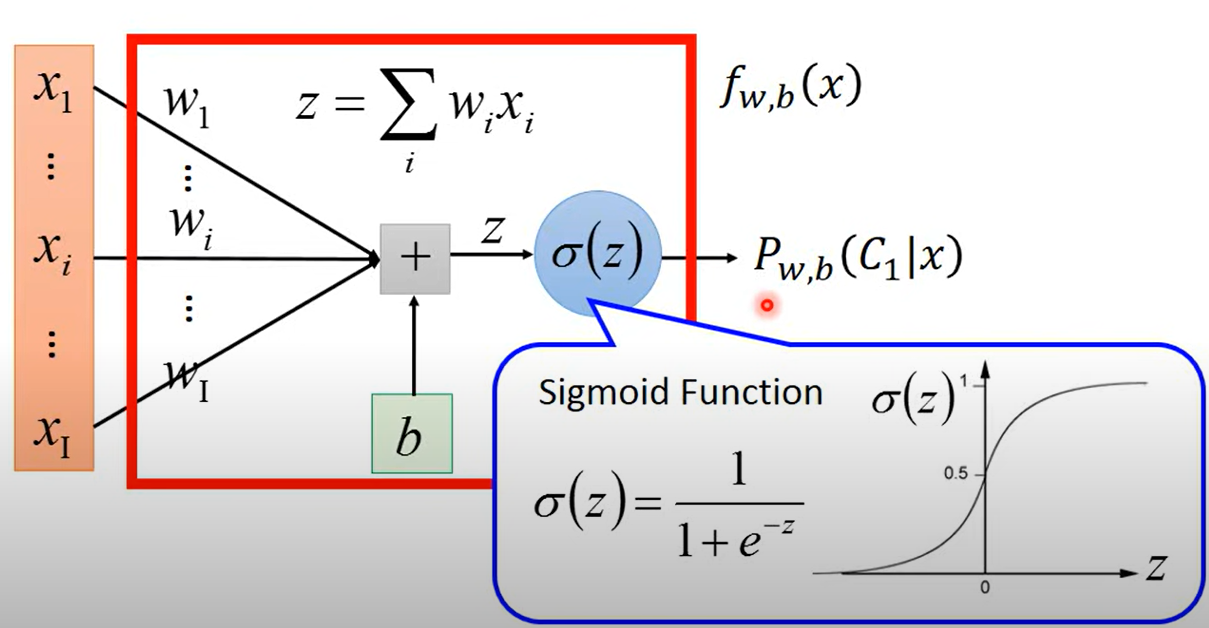
Logistic Regression

书接Classification

$$P_{w,b}(C|x)=\sigma (z)$$ $$z=\text{wcdotpx}+b$$

Logistic regression

$$f_{w,b}(x)=\sigma (\text{wx}+b)$$ $$\sigma (x)=\frac{1}{1+e^{-x}}$$

Compared to linear regression

model

• function sets
  • 函数定义不同
  • $f_{w,b}={\sum }_i{w}_i{x}_i+b$
  • $f_{w,b}(x)=\sigma (\text{wx}+b)$
  • logistic 经过了sigmoid，输出一定在0和1之间
  • linear 输出什么都行

loss function

• goodness of a function (Loss)

  • 假设训练集是$f_{w,b}(x)$产生的(即函数能描述真实数据集)，最大化概率得到最优的$w,b$
  • $Likelihood(w,b)=L(w,b)=f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))...$
  • 
  • 最大化概率等价于
  • $w^{\ast },b^{\ast }=argmi{n}_{w,b}(-lnL(w,b))$
  • 拆开转化一下
  • 
  • 
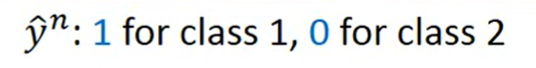
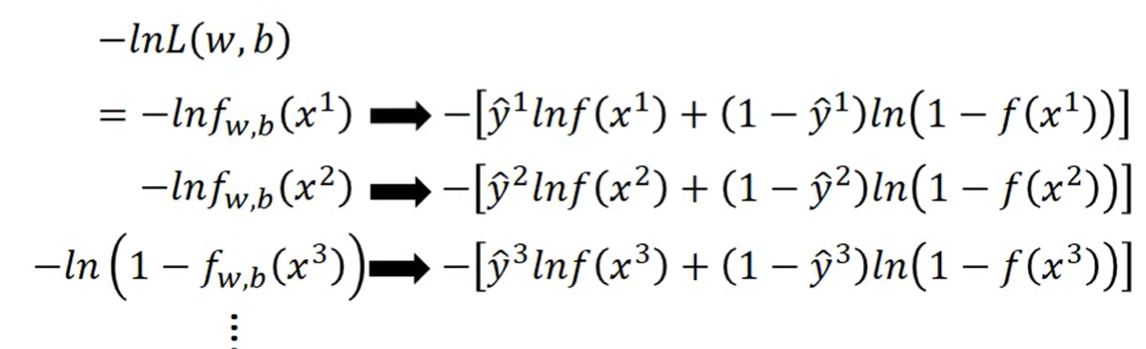
  • 就可以得到
  • 
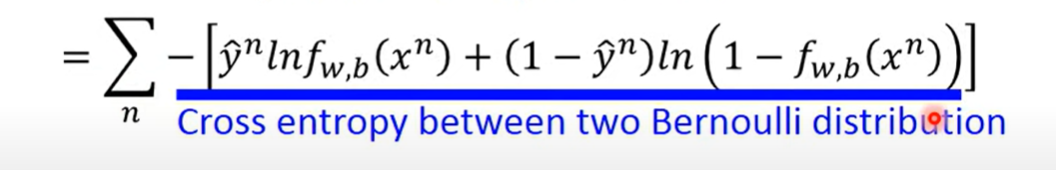
    • 这个实际上两个伯努利分布的cross-entropy
    • 
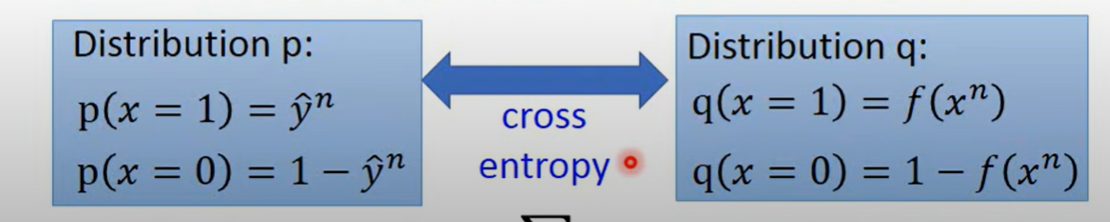
    • corss-entropy
    • $H(p.q)=-{\sum }_{x}p(x)ln(q(x))$
  • 所以loss是
  • 
  • 

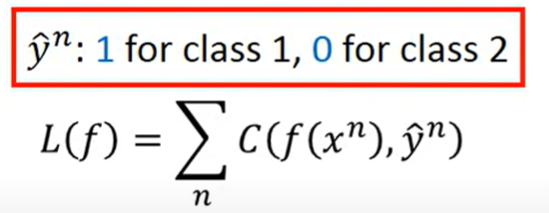
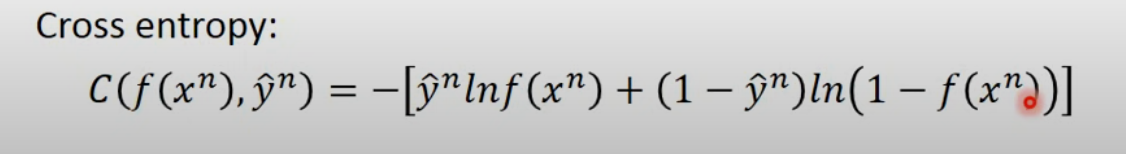
• Linear

  • Square Error
  • 
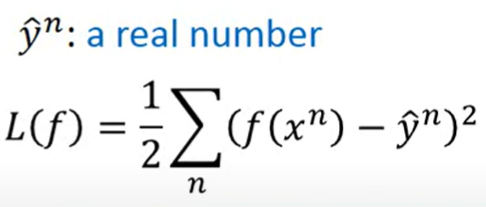
  • 两类的话

• 为什么不用一样的loss

Training

find the best function
微分

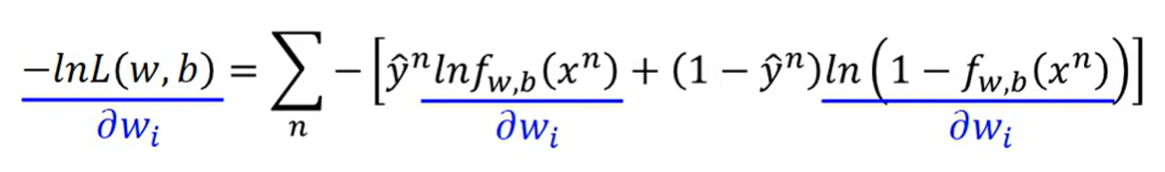
$f_{w,b}(x)$ 其实是

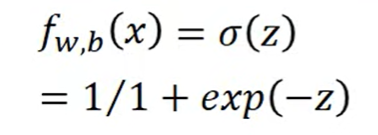
z和w有关

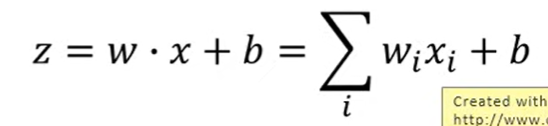
微分得

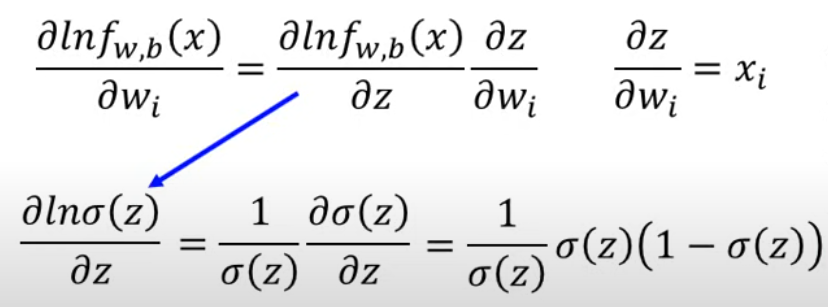
相抵消，同时$\sigma (z)=f_{w,b}(x)$

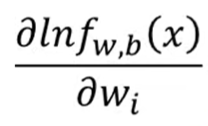
就是

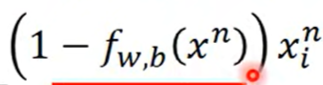
同理对后一项微分得

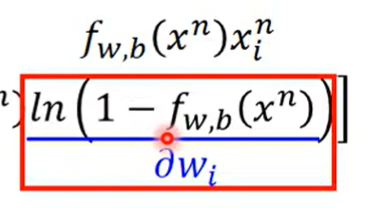
代入展开得

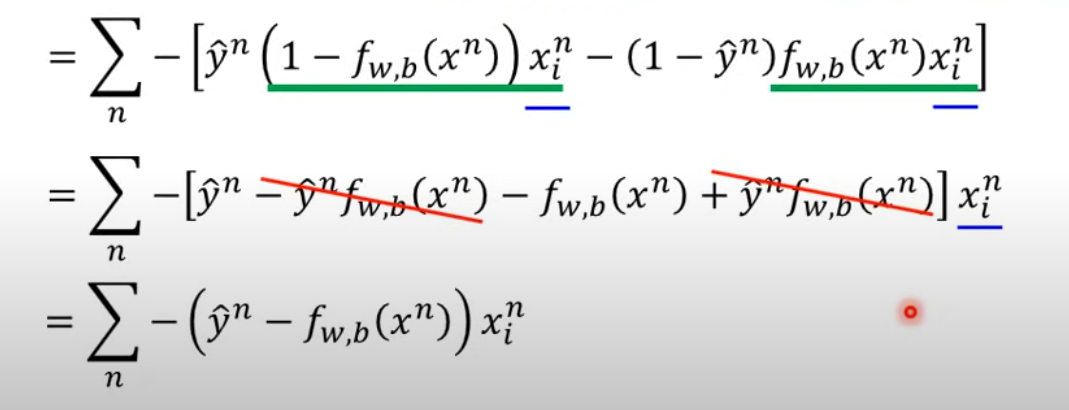
如果是Gradient descent

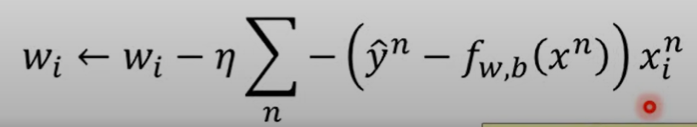
• 结果来看，参数更新取决于三件事

• 学习率$\eta$

• 训练集$x_i^n$

• 结果与实际结果的距离$({\hat{y}}^n-f_{w,b}(x^n))$

  • 距离越大更新越大

• Linear regression

  • 微分之后更新的式子
  • 
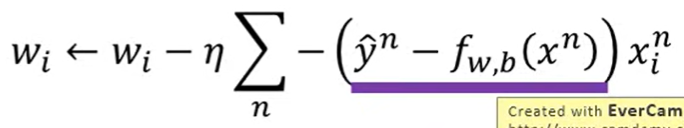
  • 一模一样啊一模一样

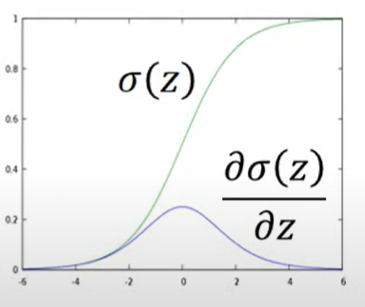
Sigmoid

sigmoid的微分可以直接背起来
$\frac{\partial \sigma }{\partial x}=\sigma (x)(1-\sigma (x))$

Why not Square Error

^c54f03 如果Logistic regression使用Square Error

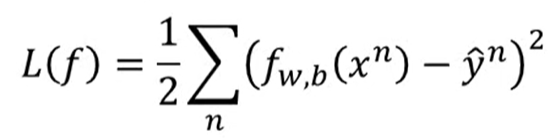
微分得到

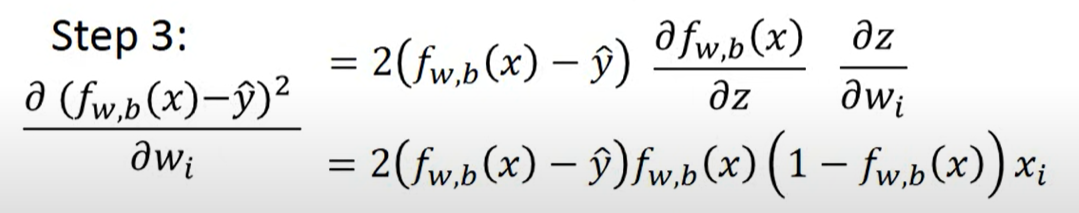
发现

• 当${\hat{y}}^n$是第一类时，
• 预测结果是第一类，和目标很近，梯度为0，很合理
• 但是如果预测结果是第二类，在另一个极端，和目标很远，梯度也为0

• 当${\hat{y}}^n$是第二类时，
• 预测结果是第一类，梯度为0
• 预测结果是第二类，梯度也为0

从本身的式子来看，当模型输出十分接近某个类别，梯度就等于0

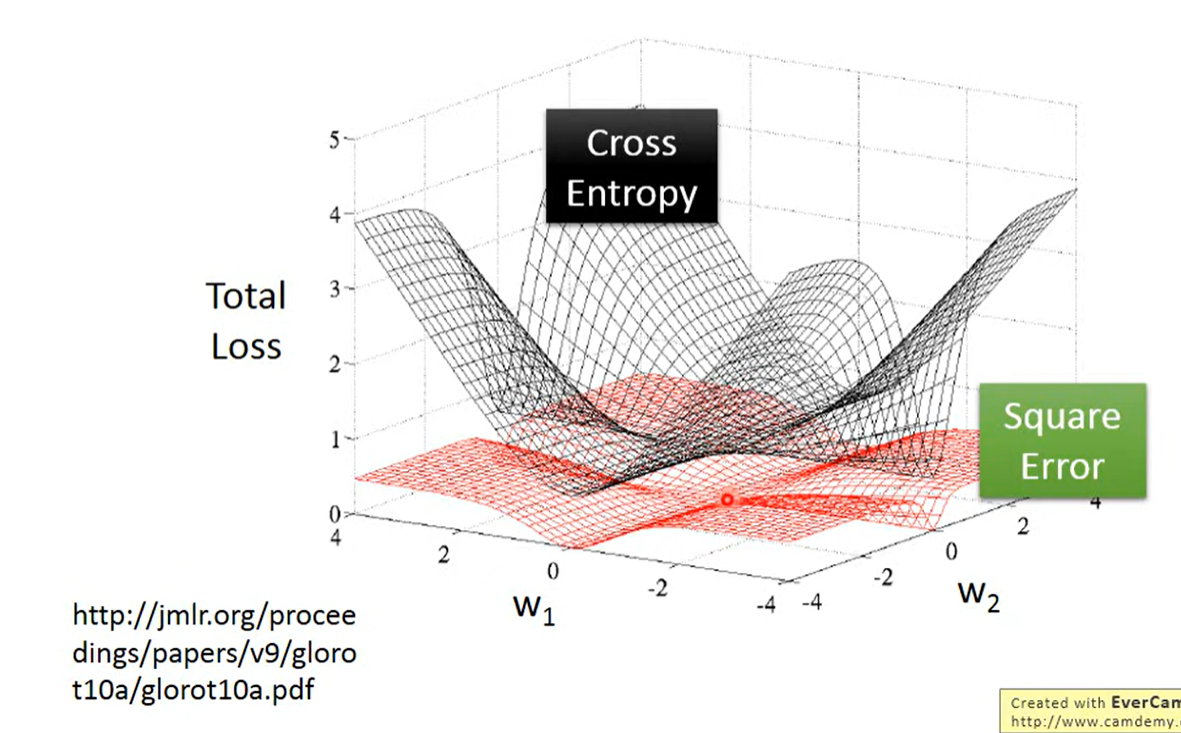
• 黑色cross-entropy，红色square error
• Cross-entropy距离越远(loss越大)，梯度越大，坡度越大，很合理
• 但是Square error，loss很大的时候是平坦的

Discriminative v.s. Generative

Logistic regression 称为 discriminative方法
两种方法的初始模型是一样的，但是假设不一样

• generative 假设数据遵循Gaussian distribution(或其他的分布假设)
• discriminative直接找$w,b$，而Generative找${\mu }^1,{\mu }^2,\Sigma$计算出$w,b$
• discriminative model 表现比较好

虽然Logistic regression可以从generaive方法推导出来，但是logistic regression并没有限制在Gaussian distribution中，推导只是证明二者在结果上等价而已。

Why dicriminative better

Generative的假设限制了模型

给定如图数据集，考虑$[1,1]$ 属于哪个类别

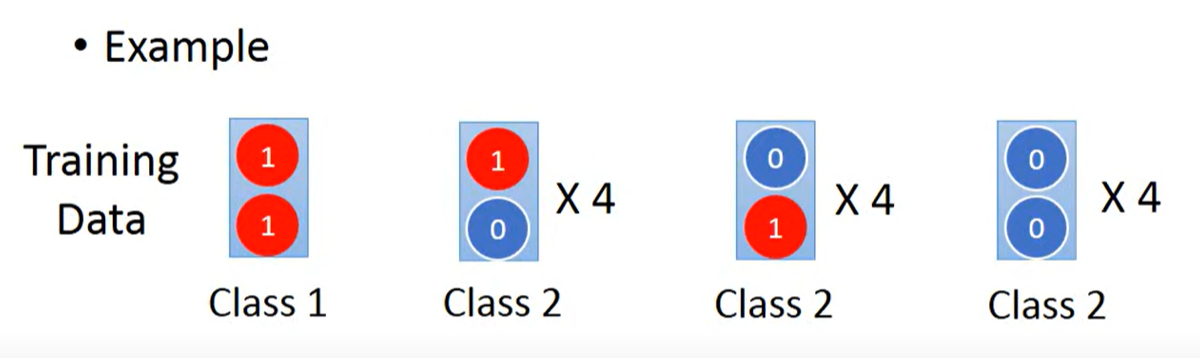
很明显是类别1，但是如果通过Naive Bayes(Generative)计算

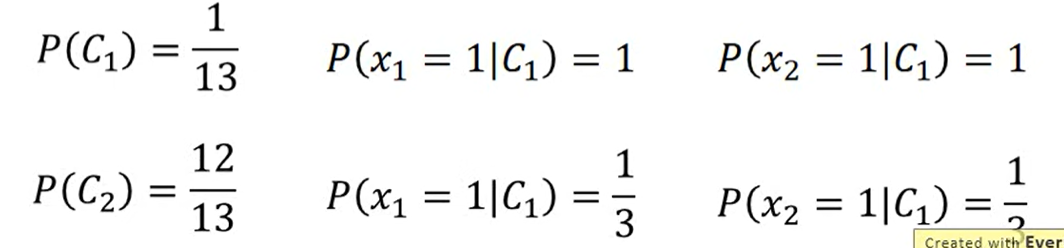
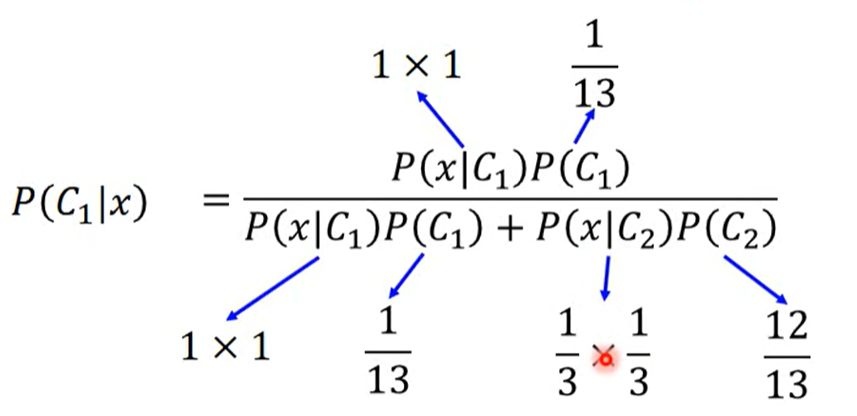
结果小于0.5，所以Naive Bayes认为$[1,1]$属于类别2

• 在Naive Bayes中，不考虑特征之间的covariance，认为每个特征是独立sample出来的
• 所以尽管$[1,1]$在类别1的数据集中出现过，并不代表$[1,1]$属于类别1，只是类别2的数据集中恰好没有sample出$[1,1]$而已

However

• 在有假设的情况下，
  • 需要的训练集越小
  • 对噪声更鲁棒
  • 假设后将模型表达式拆开，对从不同来源中学习不同参数有利(Priors and class-dependent probabilities)

Discriminative model受数据量影响更大，有时数据量少时Generative model会比较好

Multi-class classification

3 classes as example

计算$z^1,z^2,z^3$

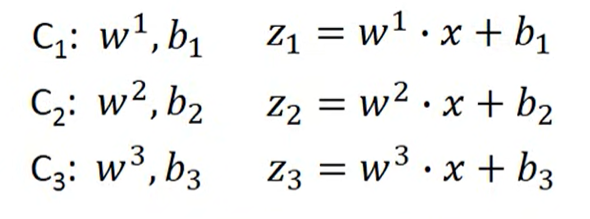
过softmax归一化

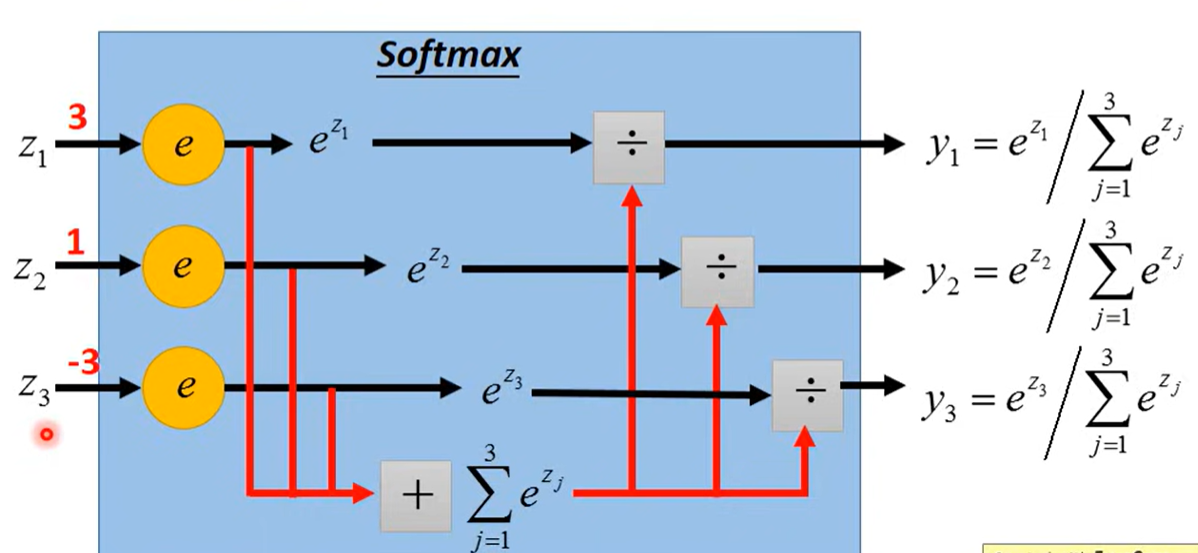
这个推导可以看 《Pattern Recogition and Machine Learning》p0.9-210 或者Maximum Entropy

然后计算cross-entropy

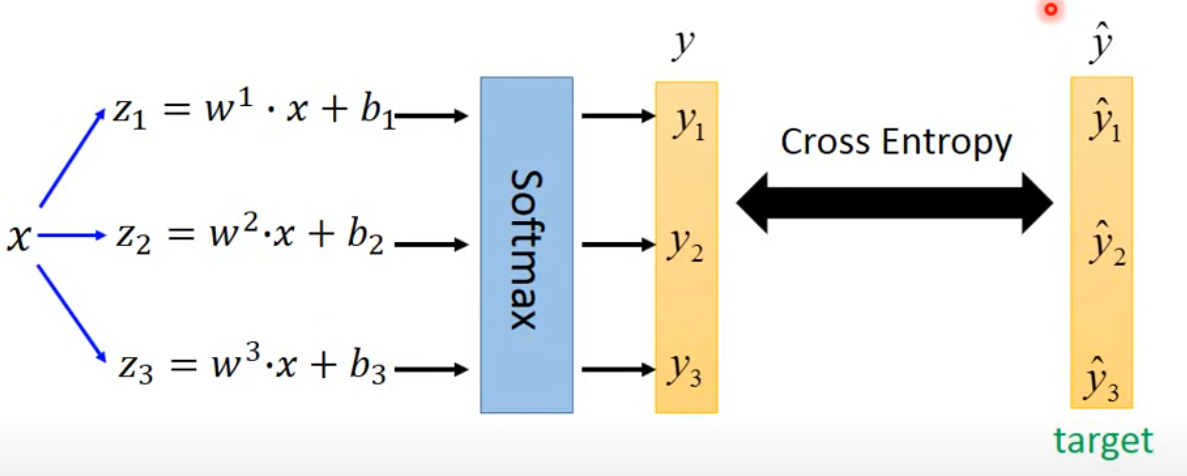
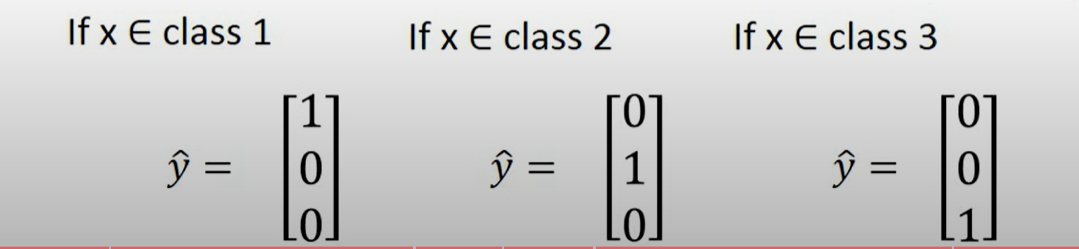
Limitation of Logistic Regression

logistic regression 是线性的函数，两个类别之间的boundary是直线

所以类别之间如果没办法被直线切分的话模型失效

此时可以使用Feature Transformation将特征变成可以被直线分割的情况

但是Feature Transformation很难做到，尝试借助机器学习来实现Feature Transformation

将经过一次logistic regression model的feature，作为一次feature transform的特征

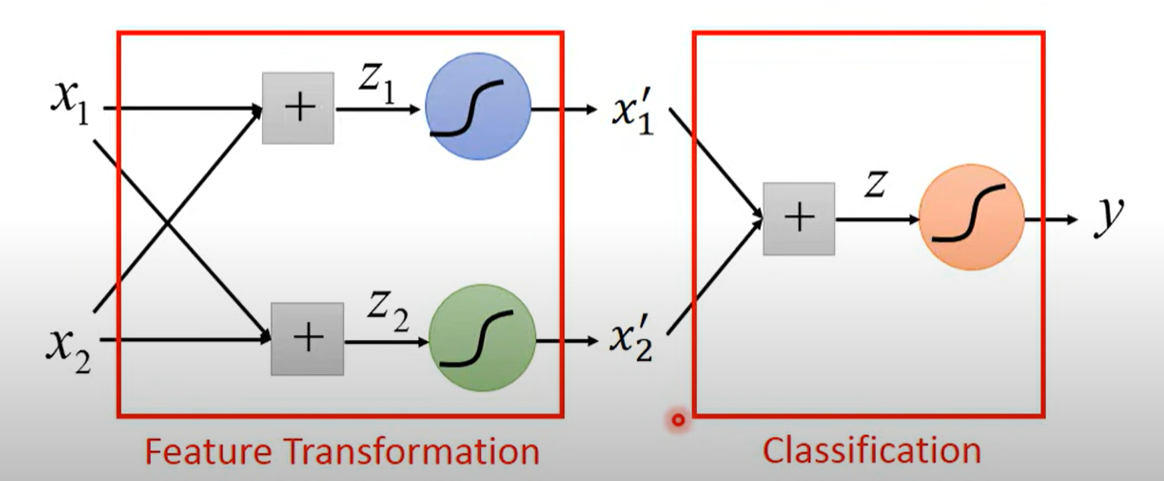
每个logistic regression称为一个neuron，合起来称为Neural Network，也就是deep Learning