Variational Autoencoder(VAE)

Generative model

old school?

Pixel RNN

2016

根据先前的pixel得到后面的pixel
用RNN做

Overview

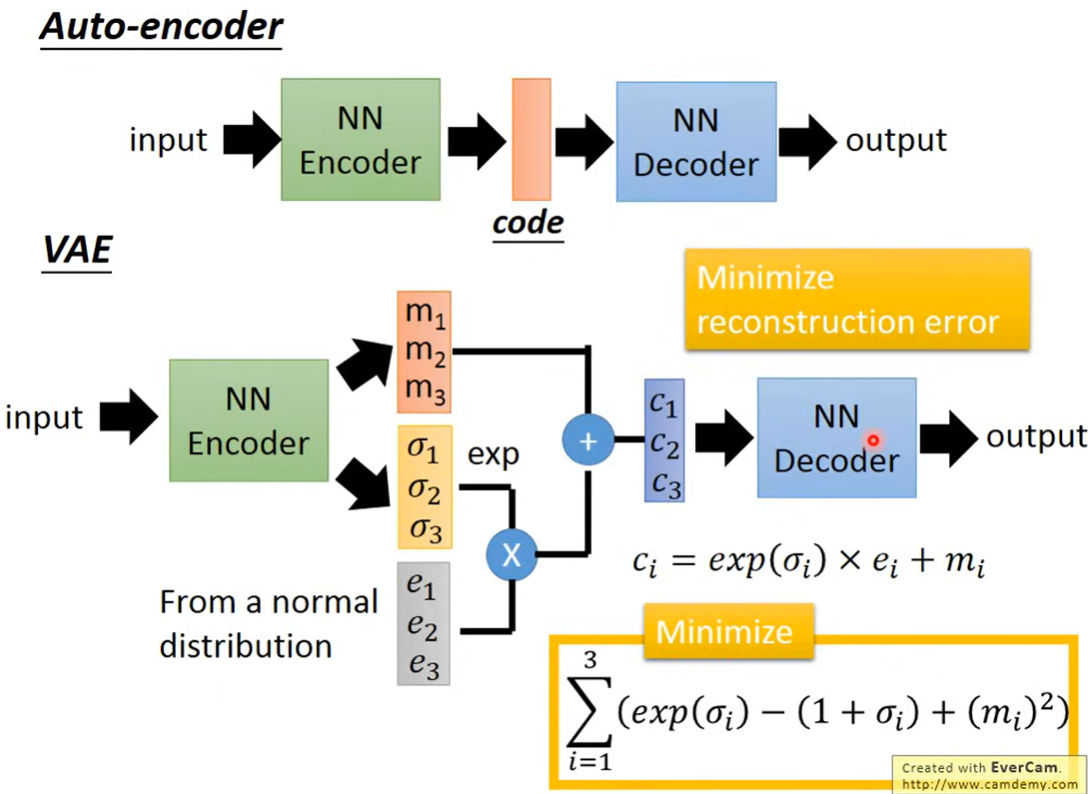
输入经过encoder生成两个向量($m,\sigma$)，然后从分布中sample出一个向量$e$，将$\sigma$取一个exp，将$e$和$\sigma$相乘，然后与$m$相加，得到$c$，然后经过decoder得到输出。
损失函数为最小化reconstruction error同时minimize右下角

Why VAE

Intuitively

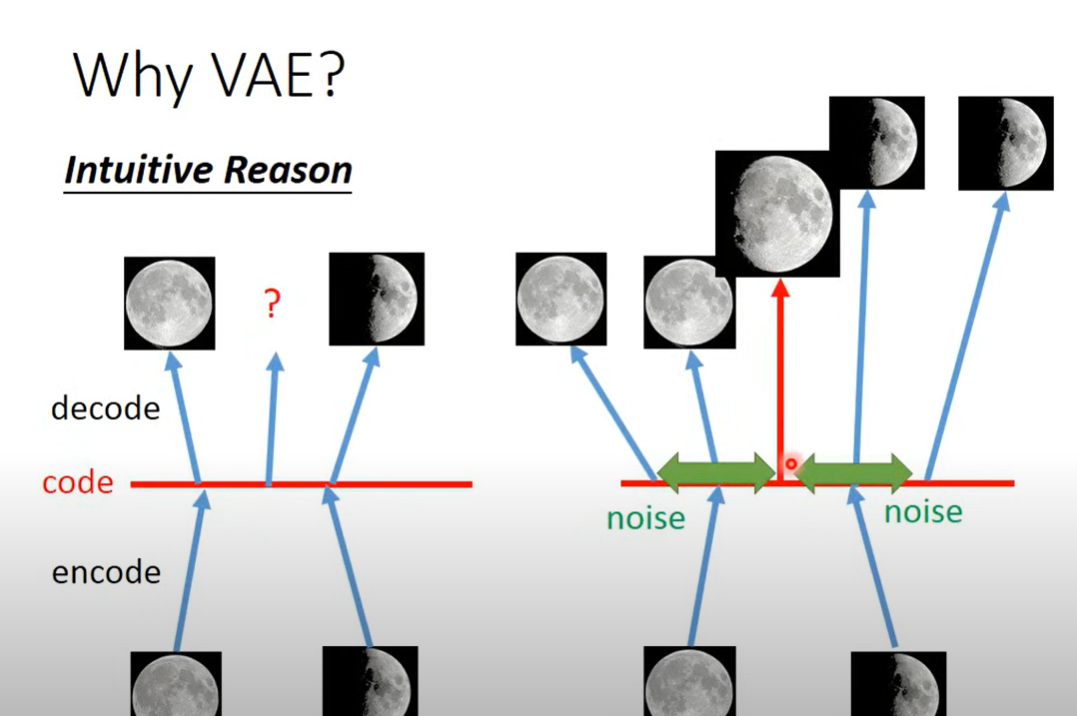
Auto encoder的话，将图片encode进一个非线性的空间中，然后decode出来，难以保证两个邻近点中间的结果会是两个点结果的权衡(在这里可能与月亮毫无关系)，如果使用VAE中间的部分被噪声覆盖，噪声交接处需要minimize两处的损失，可能就会学习到两个图像的中间态

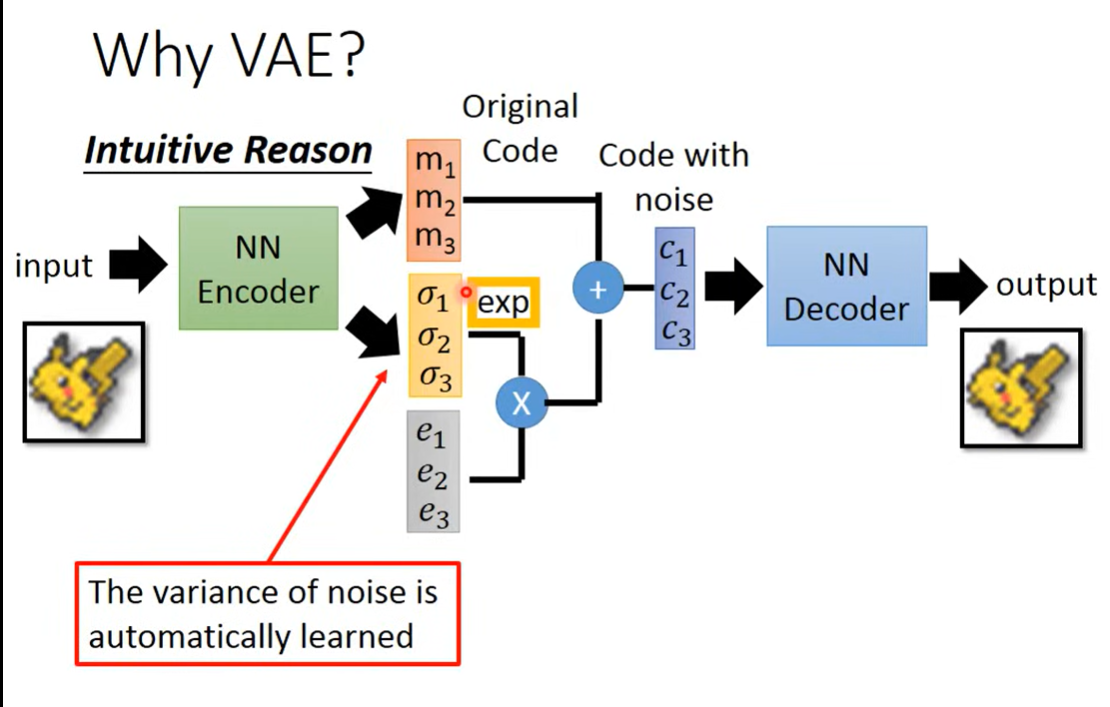
• $m$是图像的encode
• $\sigma$是噪声的variance(噪声是标准正态)，经过exp确保为正，是由模型学习出来的，所以模型会自己学会最好是多少
  • 但是如果完全自己学，出于最小化损失，会被确定为0(不再重叠，得到最小)，则需要进一步限制
  • 
  • 如果将上式画成图像
  • 
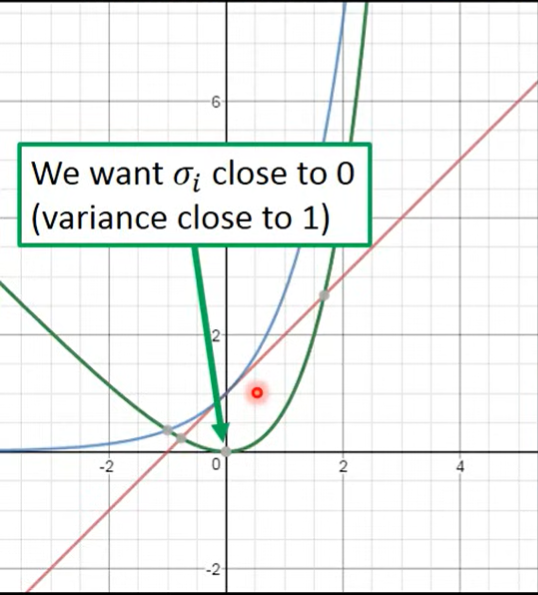
  • 蓝色是exp，红色的($1+\sigma$)，两者加减得到绿色曲线
  • 发现最小化的话，大概会取0，此时variance就是1(exp)
  • 加上与minimize reconstruction error，会得到一个权衡，使得不会选择0
  • 后面的平方项是L2 regularization
• e是高斯分布噪声

Theory

Modeling

Estimate the probability distribution(所需的图像概率大，不需要的图像概率小)

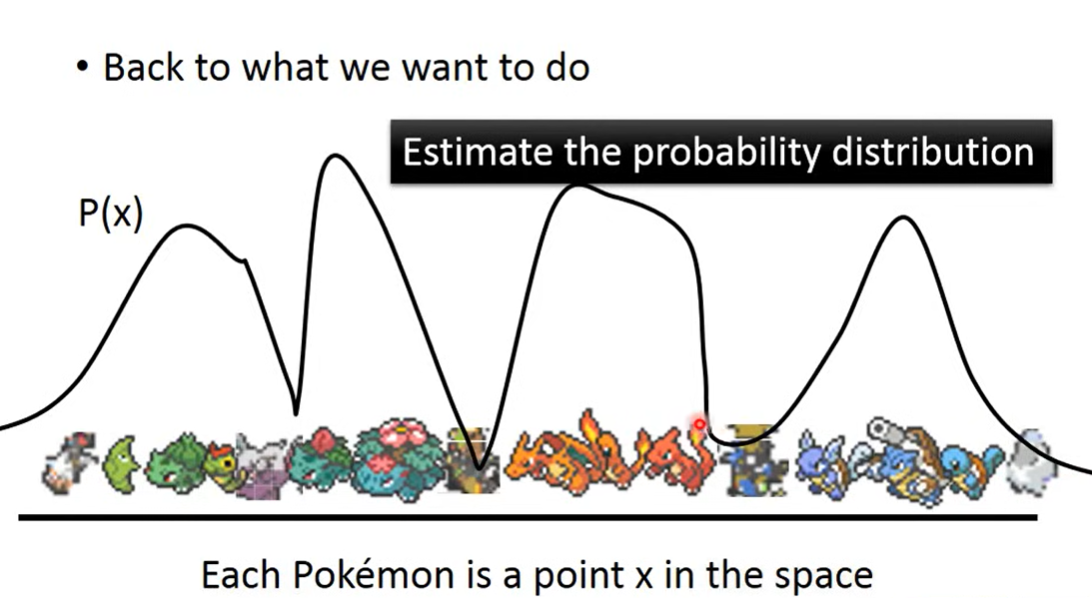
怎么得到这样一个distribution？

使用Gaussian Mixture Model
用Gasussain的组合得到复杂分布

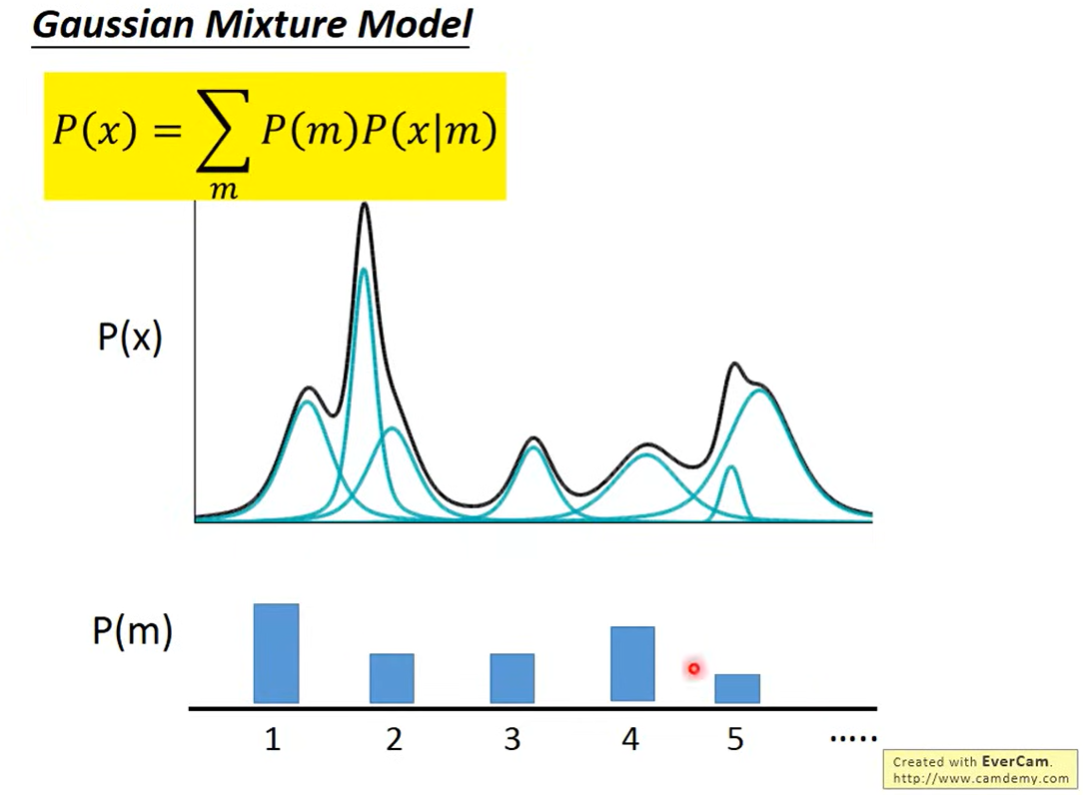
先看一下怎么从这里面sample
先选择一个m(代表哪一个Gaussian)，得到对应的Gaussian的分布，就能从这个已知的分布(知道mean和variance)中sample
应该是，通过确定的某一个Gaussian得到$P(x|m)$ ，然后再通过$P(m)$(weight)就能知道从mixture里sample出x的概率(也就是分布)

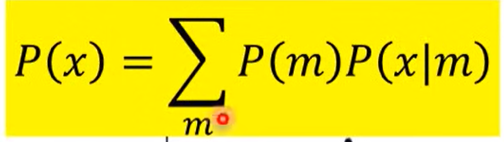
此时可以认为，每一个x都来自于一个mixture，相当于一个类别(某个位置的一组mixture)，但是只有类别的描述是不够的，需要有一个vector来描述x各个面向的特性(distributed representation)

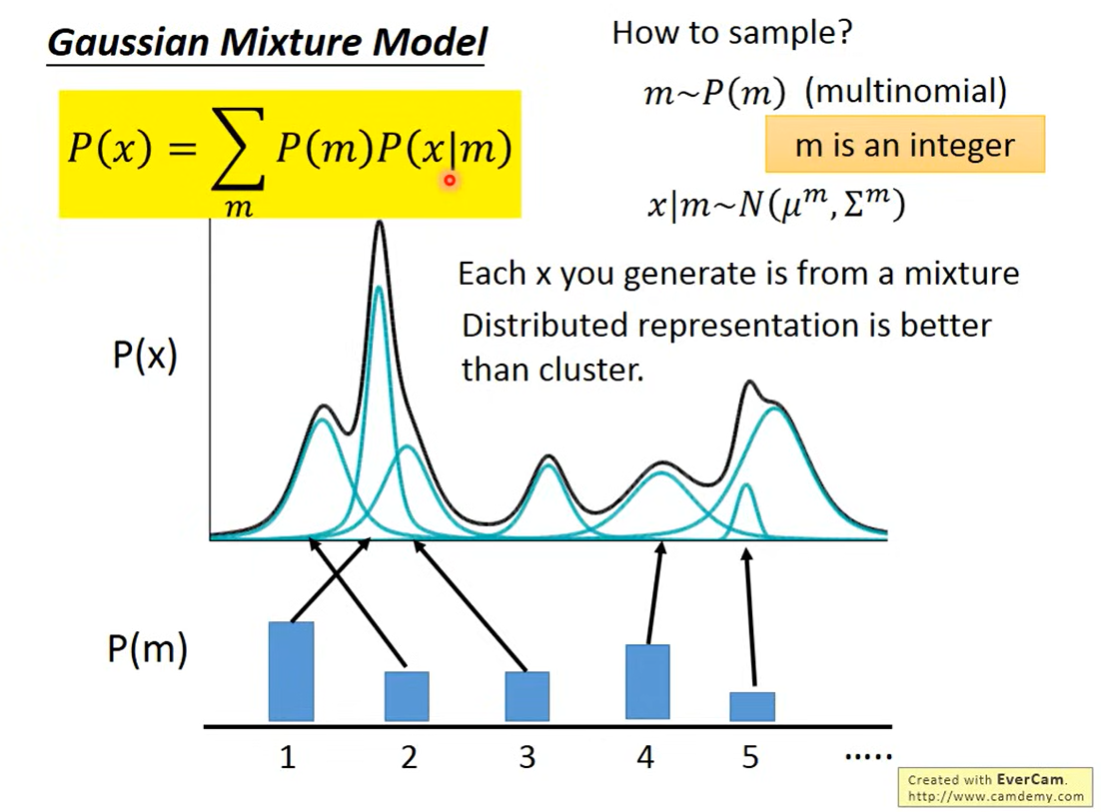
VAE可以当成是distributed representation的Gaussian mixture model

先有一个z，从normal distribution中sample出来
z是一个向量，每一维度都描述着一个特征的信息
根据 z 来决定 mean 和 variance

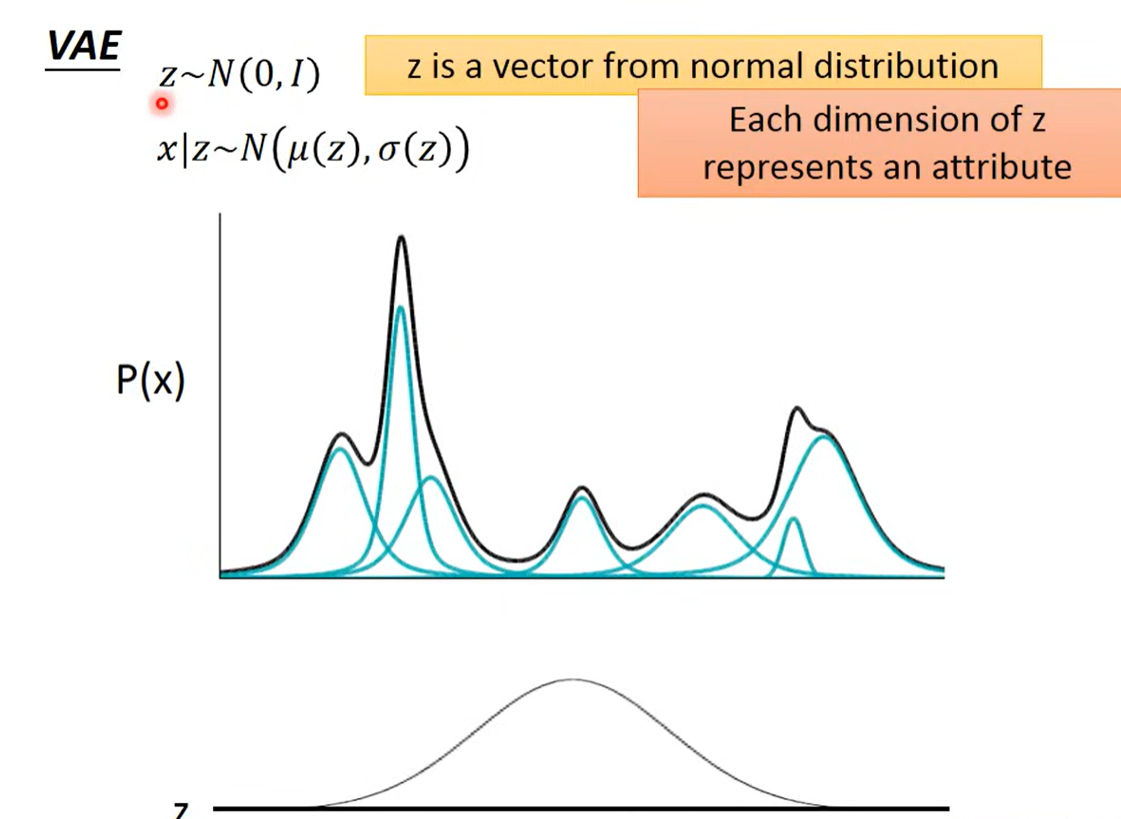
从一个假设的分布中sample出一个vector(distributed representation)，每一个维度对应着不同的特征
这个vector可以对应到Gaussian mixture model中的某一个点$x|z\sim N(\mu (z),\sigma (z))$ / 对应一个Gaussian mixture model 中的Gaussian分布
如何寻找对应的点
$\mu (z)$, $\sigma (z)$ 通过NN学习
此时的分布是

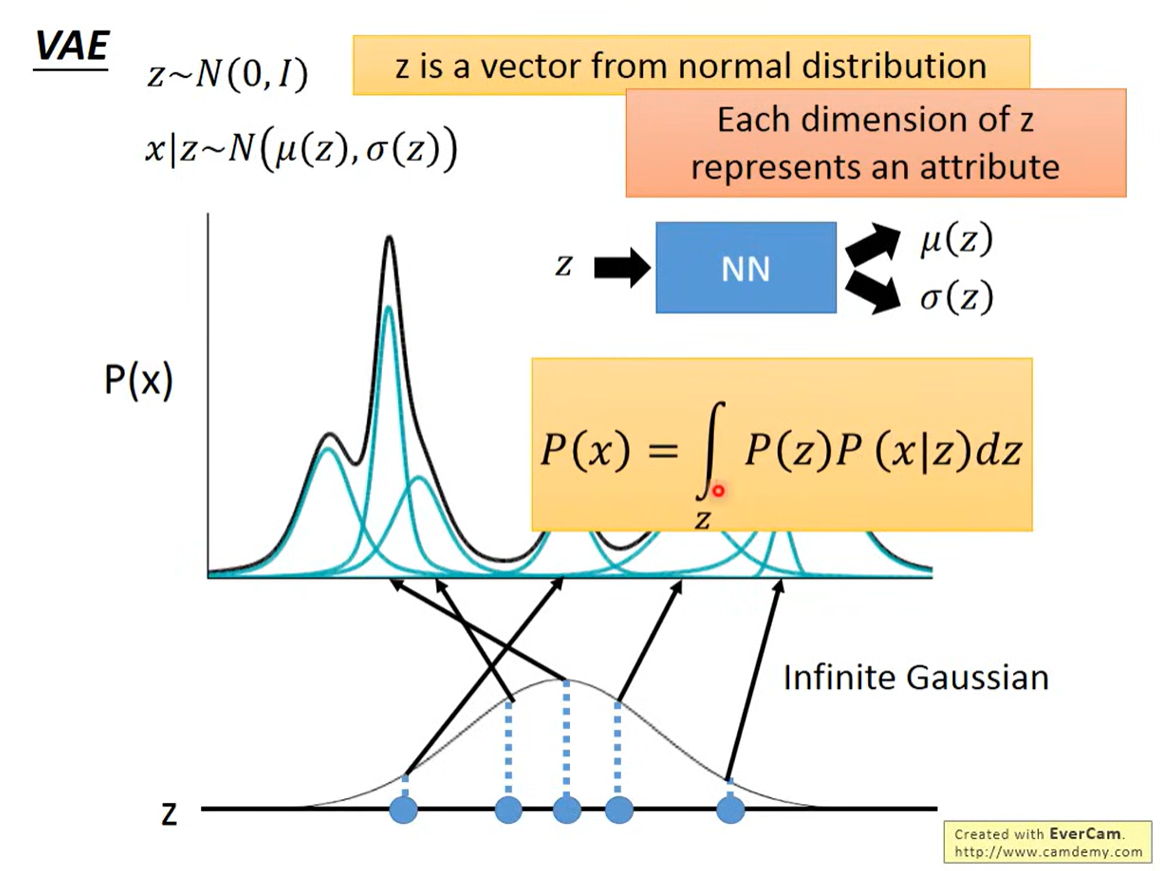
z的分布是假设的，可以是其它的分布，通过NN实现映射
此时P(x)的概率就是一个积分

training

maximize log likelihood
$L={\sum }_{x}logP(x)$
通过调整参数(调整得到的$\mu (z),\sigma (z)$)使得log likelihood 最大

完整的VAE有两个部分

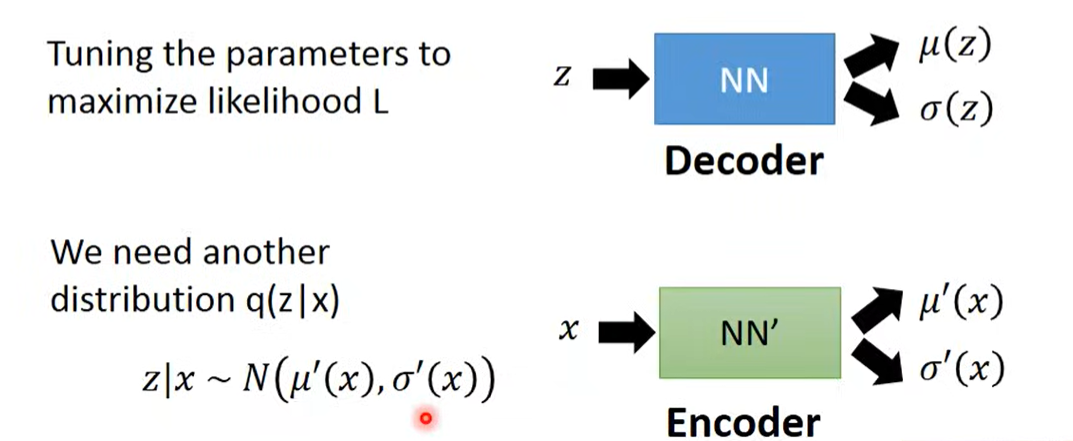
$p(x|z)$ 给定z得到x，是decoder过程，学习$z\to x$的函数
$q(z|x)$ 给定x得到z，是encoder过程，学习$x\to z$的函数

训练的时候，目标是maximize 映射的loglikelihood

经过一通变换，得到一个下界
右边的式子是一个KL divergence，一定大于0，所以左边的式子就是下界
最大化下界
由原本通过调整$P(x|z)$ 来最大化变成现在调整两个概率最大化，引入了$q(z|x)$

此时，最大化$q(z|x)$，KL divergence减小，而整体的$logP(x)$ 不变($P(x)与q(z|x)$无关)，下界$L_b$增大

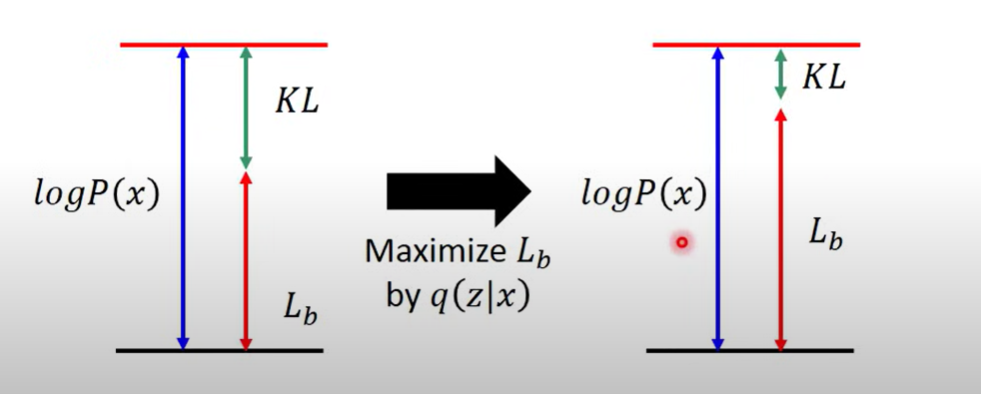
这样的话两个分布$q(z|x),p(z|x)$ 越来越接近
调整$q(z|x)$一定能减小Kl-divergence

进一步化简

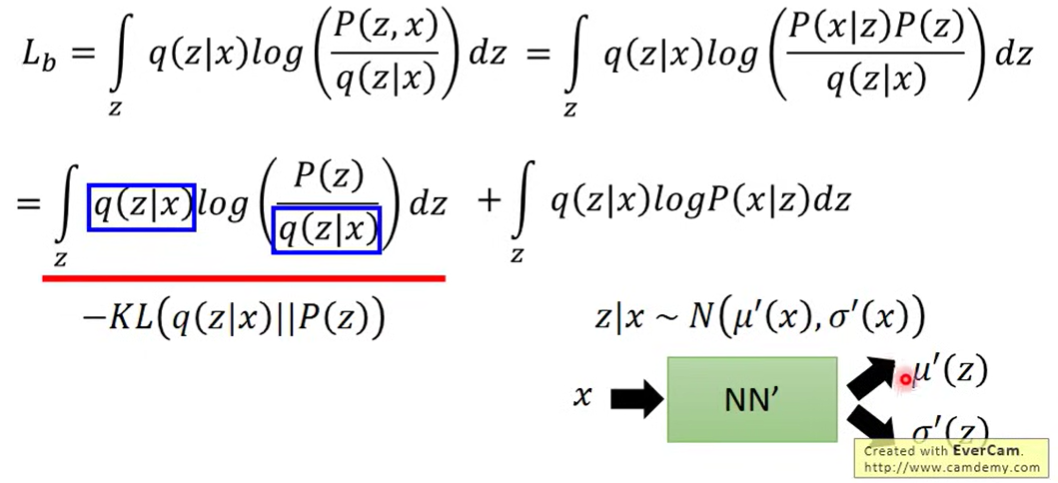
minimize 这个新的KL divergence 就是

最大化第二个式子相当于 auto-encoder
用x生成z，再用z生成x，使得概率越大越好

Problem

VAE 的目标是产生与输入相近的图像，一方面这个图像相似的衡量并不见得能够发现一些人类认为不同的细节，另一方面这样并不是真的在产生新图片