Overview
Rejection sampling(拒绝抽样),又称 acceptance-rejection method
是一种抽样方法,与MCMC,Gibbs sampling 类似,希望使用简单已知的分布对复杂或未知分布进行抽样。
Rejection sampling 或 RS 的主要思想是,利用一个简单的已知分布,即proposal distribution 覆盖目标分布 target distribution,进行两次抽样:首先在proposal distribution上进行抽样,然后通过在均匀分布上进行抽样来对抽取的样本进行接受/拒绝决策
数学表达如下:
其中
- 是目标分布
- 是proposal distribution
- 是常数,用于调整 使得 覆盖
- 如果满足条件则接受,否则拒绝进行下一次抽样
How does it work?
假设目标分布如下:
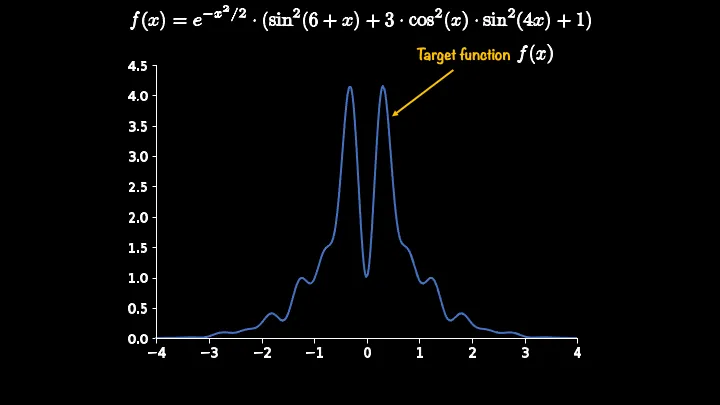
我们希望从-3到3进行抽样,但是目标分布过于复杂,于是我们选择proposal distribution为均匀分布
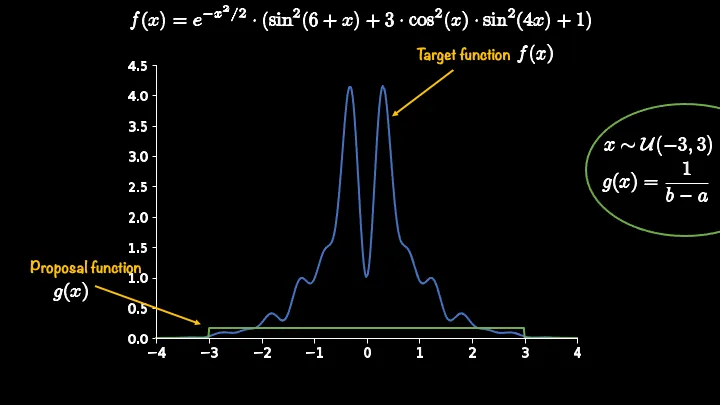
将均匀分布进行缩放,即选择常数,使得proposal distribution覆盖目标分布
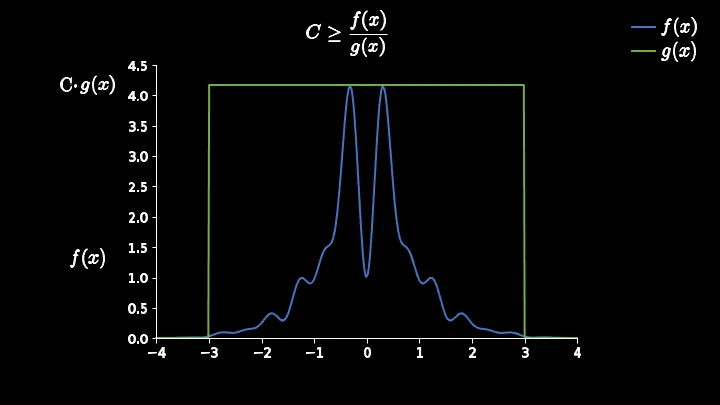
从proposal distribution 中抽样,作为从目标分布进行采样的候选
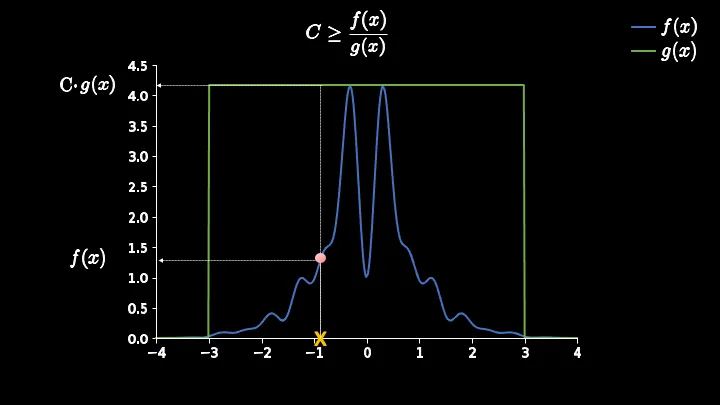
我们希望最终的目的是按照目标分布进行采样,也就是尽可能遵循目标分布的概率,当目标分布概率大时,样本被抽中的概率大。单纯使用proposal distribution无法完成这一点。
于是我们需要对抽样得到的样本进行筛选,引入接受/拒绝的决策
一种可行的方法是
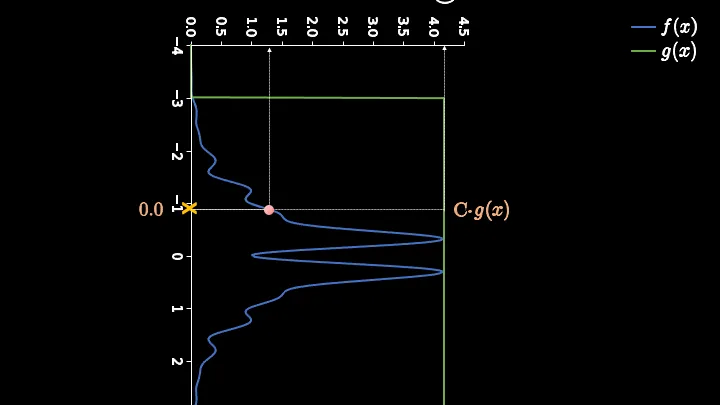
用一个均匀分布,,如果抽样得到的落在内,即目标分布内,则接受,落在外面,即内,则拒绝。
数学表达为
对归一化可得
落在内的概率,在这个例子中,随增大而增大
可以看出,虽然我们选择的相当简单,而且与原分布差异明显,但是通过接受拒绝的修正,我们相当于调整了 在各处的权重,使得抽样结果接近目标分布
Limitations
- 尽管简单直观,但是选择一个合适的proposal distribution和常数K是比较困难的
- 需要已知目标分布的PDF(probability density function)
- 抽取到的样本不一定接受,导致抽样的效率不高