PF-ODE

虽然标题是PF-ODE，但是废物的我应该从DDPM开始回顾

DDPM是怎么想的

一般认为DDPM是Diffusion开山作
DDPM希望将模型生图的过程拆分为前向加噪过程和反向去噪过程，通过马尔可夫链的假设，DDPM为前向加噪进行建模

$$q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})=\mathcal{N}({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I})q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)=\prod _{t=1}^{T}q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})$$

在这样的建模中

• 下一个状态只与前一个状态有关
• 基于正态分布，使得前向反向过程都在正态分布的假设下
• $\sqrt{1-{\beta }_t}$ 和 ${\beta }_t$ 的中$\beta$为超参数，这样的加噪方式能够通过重参数化技巧简化 $x_t$的计算

然后在反向去噪过程(denoising process)
我们希望能够得到分布 $p(x_{t-1}|x_t)$ 这个分布仍是高斯分布，则我们需要通过模型逐步建模反向过程

$$p({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)=\mathcal{N}({\mathbf{x}}_{t-1};\mathbf{\mu }({\mathbf{x}}_t,t),\mathbf{\Sigma }({\mathbf{x}}_t,t))$$ $$p_{\theta }({\mathbf{x}}_{0:T})=p({\mathbf{x}}_T)\prod _{t=1}^T{p}_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)=\mathcal{N}({\mathbf{x}}_{t-1};{\mu }_{\theta }({\mathbf{x}}_t,t),{\mathbf{\Sigma }}_{\theta }({\mathbf{x}}_t,t))$$

关键难点在 $p(x_{t-1}|x_t)$，根据贝叶斯公式，我们需要知道 $p(x_t),p(x_{t-1})$ 才能进行计算，即需要完整的数据分布$\tilde{p}(x_0)$，$p(x_t)=\int p(x_t|x_0)\tilde{p}(x_0)d{x}_0$
我们可以通过加入condition $x_0$ 来进行估计

$$q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)=\mathcal{N}({\mathbf{x}}_{t-1};\tilde{\mu }({\mathbf{x}}_t,{\mathbf{x}}_0),{\tilde{\beta }}_t\mathbf{I})$$

根据贝叶斯公式，有

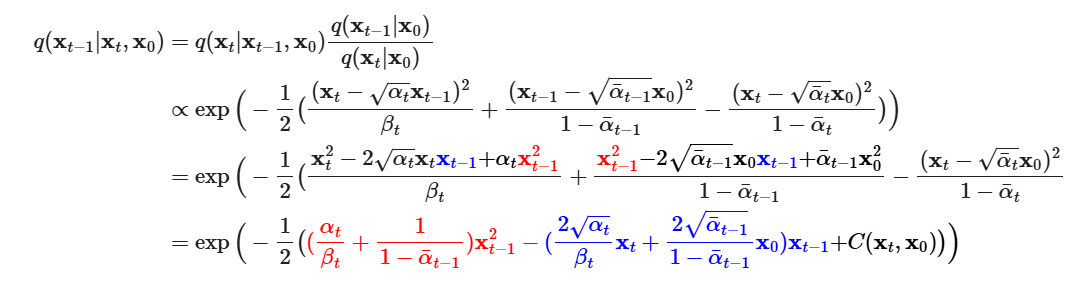
由此得到方差和期望

$${\tilde{\beta }}_t=1/(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})=1/(\frac{{\alpha }_t-{\bar{\alpha }}_t+{\beta }_t}{{\beta }_t(1-{\bar{\alpha }}_{t-1})})=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t$$ $$\begin{array}{rl}{\tilde{\mu }}_t({\mathbf{x}}_t,{\mathbf{x}}_0)& =(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0)/(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})\\ & =(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0)\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t\\ & =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\bar{\beta }}_t}{1-{\bar{\alpha }}_t}{\mathbf{x}}_0\end{array}$$

DDPM固定方差(通过指定$\beta$)，期望直接预测期望来进行预测
根据重参数化trick，进一步得到期望的表达式

$$\begin{array}{l}{\tilde{\mu }}_t=\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}\frac{1}{\sqrt{{\bar{\alpha }}_t}}({\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_t)\\ =\frac{1}{\sqrt{{\alpha }_t}}\left(x_t-\frac{1-a_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_t\right)\end{array}$$

此时只有 $ϵ$ 是未知的，在这里可以直接让模型预测这个噪声，就可以顺理成章地得到DDPM的训练损失和推理过程
但是这样略显草率，更严格来说，我们的目标是极大化似然函数
根据ELBO技巧，我们可以得到

$$\begin{array}{rl}{L}_{CE}& =-{\mathbb{E}}_{q(x_0)}\log p_{\theta }(x_0)\\ & =-{\mathbb{E}}_{q(x_0)}\log \left(\int p_{\theta }(x_{0:T})d{x}_{1:T}\right)\\ & =-{\mathbb{E}}_{q(x_0)}\log \left(\int q(x_{1:T}|x_0)\frac{p_{\theta }(x_{0:T})}{q(x_{1:T}|x_0)}d{x}_{1:T}\right)\\ & =-{\mathbb{E}}_{q(x_0)}\log \left({\mathbb{E}}_{q(x_{1:T}|x_0)}\left[\frac{p_{\theta }(x_{0:T})}{q(x_{1:T}|x_0)}\right]\right)\\ & \le -{\mathbb{E}}_{q(x_{0:T})}\log \frac{p_{\theta }(x_{0:T})}{q(x_{1:T}|x_0)}\\ & ={\mathbb{E}}_{q(x_{0:T})}\left[\log \frac{q(x_{1:T}|x_0)}{p_{\theta }(x_{0:T})}\right]=L_{VLB}\end{array}$$

$L_{VLB}$ 可以拆分成几项KL散度加和

$${\mathbb{E}}_q[\underset{L_T}{\underbrace{D_{\mathrm{KL}}(q({\mathbf{x}}_T|{\mathbf{x}}_0)\parallel p_{\theta }({\mathbf{x}}_T))}}+\sum _{t=2}^T\underset{L_{t-1}}{\underbrace{D_{\mathrm{KL}}(q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)\parallel p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t))}}-\underset{L_0}{\underbrace{\log p_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)}}]$$

第一项可忽略，重点是中间项，对于已知的高斯分布的KL散度，有解析解，代入得到

$$\begin{array}{rl}{L}_t& ={\mathbb{E}}_{x_0,ϵ}\left[\frac{1}{2||{\Sigma }_{\theta }(x_t,t)|{|}^2}||{\tilde{\mathbf{\mu }}}_{\theta }({\mathbf{x}}_t,t)-\mathbf{\mu }({\mathbf{x}}_t,t)|{|}^2\right]\\ & ={\mathbb{E}}_{x_0,ϵ}\left[\frac{1}{2||{\Sigma }_{\theta }|{|}^2}||\frac{1}{\sqrt{{\alpha }_t}}\left({\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}\mathbf{ϵ}\right)-\frac{1}{\sqrt{{\alpha }_t}}\left({\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)\right)|{|}^2\right]\\ & ={\mathbb{E}}_{x_0,ϵ}\left[\frac{(1-{\alpha }_t{)}^2}{2{\alpha }_t(1-{\bar{\alpha }}_t)||{\Sigma }_{\theta }|{|}^2}||\mathbf{ϵ}-{\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)|{|}^2\right]\\ & ={\mathbb{E}}_{x_0,ϵ}\left[\frac{(1-{\alpha }_t{)}^2}{2{\alpha }_t(1-{\bar{\alpha }}_t)||{\Sigma }_{\theta }|{|}^2}||\mathbf{ϵ}-{\mathbf{ϵ}}_{\theta }(\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}\mathbf{ϵ},t)|{|}^2\right]\end{array}$$

DDPM实践中发现化简效果更佳

$$\begin{array}{rl}{L}_t^{\mathrm{simple}}& ={\mathbb{E}}_{t\sim [1,T],{\mathbf{x}}_0,{ϵ}_t}[\Vert {\mathbf{ϵ}}_t-{\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t){\Vert }^2]\\ & ={\mathbb{E}}_{t\sim [1,T],{\mathbf{x}}_0,{ϵ}_t}[\Vert {\mathbf{ϵ}}_t-{\mathbf{ϵ}}_{\theta }(\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}{\mathbf{ϵ}}_t,t){\Vert }^2]\end{array}$$

到这里我们训练了一个模型预测噪声，然后回到上面求出的均值和方差就可以逐步生成

DDIM 又是什么

在上面DDPM的推导中，有一步是 $p(x_{t-1}|x_t,x_0)$ 的分布推导。使用重参数化方法之后，我们消去了$x_0$来求解均值
有一种想法是，如果我们能够通过$x_t$估计$x_0$并代入式子的话，是否也可以得到需要求解的结果
则我们希望训练一个模型，用模型的输出 $\bar{\mu }(x_t)$ 来预估 $x_0$，损失设为 $||x_0-\bar{\mu }(x_t)|{|}^2$
再次通过重参数化方法改写 $x_0$ 和 $\bar{\mu }(x_t)$(当成$x_0$ 来替换)，这样仍然能将$||x_0-\bar{\mu }(x_t)|{|}^2$推导成类似的损失函数(见苏神生成扩散模型漫谈（三）：DDPM = 贝叶斯 + 去噪 - 科学空间|Scientific Spaces)
这样的做法和DDIM有相似的地方

Diffusion process

按照原论文的说法，DDIM 的核心观察是 DDPM的损失只依赖于forward过程的边际分布 $q(x_t|x_0)$，而不直接依赖于联合分布 $q(x_{1:T}|x_0)$，实际上应该就是不依赖于$q(x_t|x_{t-1})$
基于此，我们可以尝试改写前向过程为非马尔可夫链形式
根据贝叶斯公式

$$q_{\sigma }(x_t|x_{t-1},x_0)=\frac{q_{\sigma }(x_{t-1}|x_t,x_0)q_{\sigma }(x_t|x_0)}{q_{\sigma }(x_{t-1}|x_0)},$$

根据representation trick，有$q_{\sigma }(x_t|x_0)=\mathcal{N}(\sqrt{{\alpha }_t}{x}_0,(1-{\alpha }_t)I)$
也有

$$\begin{array}{rl}{\mathbf{x}}_{t-1}& =\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_{t-1}}{\mathbf{ϵ}}_{t-1}\\ & =\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_{t-1}-{\sigma }_t^2}{\mathbf{ϵ}}_t+{\sigma }_t\mathbf{ϵ}\end{array}$$

和反解 $ϵ$ 得到的 ${ϵ}_t=\frac{x_t-\sqrt{{\alpha }_t}{x}_0}{\sqrt{1-{\alpha }_t}}$，代入得到分布 $q_{\sigma }(x_{t-1}|x_t,x_0)$

$$q_{\sigma }(x_{t-1}|x_t,x_0)=\mathcal{N}\left(\sqrt{{\alpha }_{t-1}}{x}_0+\sqrt{1-{\alpha }_{t-1}-{\sigma }_t^2}\cdot \frac{x_t-\sqrt{{\alpha }_t}{x}_0}{\sqrt{1-{\alpha }_t}},{\sigma }_t^{2}I\right)$$

这样贝叶斯公式中的所有分布都已知，此时的前向process依赖于$x_{t-1},x_0$，也就不再是马尔可夫链，这里也可以看到反向过程的分布的随机性由$\sigma$控制，$\sigma$ 是不受限制的，当趋近于0时，整个过程趋于确定

Generative process

就像上面DDPM 苏神的一个角度中说的，我们考虑能不能直接预测$x_0$来建模
根据重参数化方法+使用模型预测噪声，我们可以得到

$$f_{\theta }^{(t)}(x_t):=\frac{x_t-\sqrt{1-{\alpha }_t}\cdot {ϵ}_{\theta }^{(t)}(x_t)}{\sqrt{{\alpha }_t}}.$$

将其代入反向过程，得到decode distribution

$$p_{\theta }^{(t)}(x_{t-1}\mid x_t)=\{\begin{array}{ll}\mathcal{N}(f_{\theta }^{(1)}(x_1),{\sigma }_1^{2}I)& \text{if }t=1,\\ q_{\sigma }(x_{t-1}\mid x_t,f_{\theta }^{(t)}(x_t))& \text{otherwise},\end{array}$$

此时我们引入了$\sigma$，改变了两个分布，损失形式仍为VLB，但与DDPM略有不同

$$\begin{array}{rl}{J}_{\sigma }({ϵ}_{\theta })& :={\mathbb{E}}_{{\mathbf{x}}_{0:T}\sim q_{\sigma }({\mathbf{x}}_{0:T})}[\log q_{\sigma }({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)-\log p_{\theta }({\mathbf{x}}_{0:T})]\\ & ={\mathbb{E}}_{{\mathbf{x}}_{0:T}\sim q_{\sigma }({\mathbf{x}}_{0:T})}[\log q_{\sigma }(x_T|x_0)+\sum _{t=2}^T\log q_{\sigma }(x_{t-1}|x_t,x_0)-\sum _{t=1}^T\log p_{\theta }^{(t)}(x_{t-1}|x_t)-\log p_{\theta }(x_T)]\end{array}\text{\hspace{1em}(11)}$$

论文提到，$\text{For all }\sigma >0\text{, there exists }\gamma \in {\mathbb{R}}_{>0}^T\text{ and }C\in \mathbb{R}\text{, such that }{J}_{\sigma }=L_{\gamma }+C\text{.}$ $L_{\gamma }$ 当前置的权重系数$\gamma$原本受限于时间$t$，DDIM论文证明当每个$t$，模型参数不共享的话有最优解相同，我的理解是实际训练的时候并不考虑所有时间步而是单个项进行优化，此时无所谓权重系数所以直接取1。在上述定理下，优化$L_{\sigma }$和优化$L_1$有时相同(论文这么说)，所以认为二者等价，DDIM可以直接使用DDPM的损失

Speed up

当${\sigma }_t$对所有$t$ 取0 的时候，会得到一个implicit probabilistic model(无法显式写出概率密度函数，模型由一个采样过程定义)。
DDIM认为，既然$L_1$ 丝毫不依赖于T时间步的forward process，为何不选取一个T的子集来进行forward 和 generate
定义一个子集 $x_{\tau 1},x_{\tau 2},x_{\tau 3},...x_{\tau S}$ ，每个$\tau i$是increasing的subsequence of $[1,..T]$
如果$S$ 小于 $T$ significantly，那么我们就可以极大的减少inference时的computational cost
采样方法是

$$x_{t-1}=\sqrt{{\bar{\alpha }}_{t-1}}{x}_0+\sqrt{1-{\bar{\alpha }}_{t-1}-{\eta }^2{\sigma }_t^2}{ϵ}_0(x_t,t)+\eta \cdot {\sigma }_t\cdot z$$

实际应用时，设置 ${\sigma }_t^2$ 为

$${\sigma }_t^2=\eta \cdot {\tilde{\beta }}_t=\eta \cdot \sqrt{(1-{\alpha }_{t-1})/(1-{\alpha }_t)}\sqrt{(1-{\alpha }_t/{\alpha }_{t-1})}$$

当$\eta =1$，与DDPM相同；当$eta=0$时，过程完全确定

另外的，论文设置了两种时间步的采样方法

• linear ${\tau }_i=[ci]$
• quadratic ${\tau }_i=[c{i}^2]$
• 两种方法$ci$的设定都使得最后一个时间步接近于 $T$

DDIM论文中给出了ODE的关系，我们先跳过这一段最后再回来看

SDE框架

内容不完全，最好参考这一篇很好的入门博客Diffusion学习笔记（三）——随机微分方程（SDE）
作为一个废物我需要先跟着过一下基础知识，基本是抄下来的，再写一遍帮助自己梳理一下知识

随机微分方程首先涉及了随机过程的微积分概念，所以我们先从连续开始定义

均方微积分

定义3.1:(均方收敛) 设随机变量序列 $X_n,n=1,2,...$ 和随机变量 $X$ 的二阶矩有限(二次幂的期望存在)，若均方极限

$$\underset{n\to \infty }{\lim }E|X_n-X{|}^2=0$$

称$X_n$均方收敛于X，记作 $l.i.m_{n\to \infty }{X}_n=X$ ($l.i.m$ 为limit in mean square)或 $X_n\stackrel{m.s}{\to }X$
定理3.1：若均方收敛，普通极限(期望的极限)和均方极限(均方极限的期望)在期望下可以交换位置
若 ${\text{l.i.m.}}_{n\to \infty }{X}_n=X$

$$\underset{n\to \infty }{\lim }E(X_n)=E({\text{l.i.m.}}_{n\to \infty }{X}_n)$$

证明：由$D(Y)=E{Y}^2+E^{2}Y$，可以得到 $E^{2}Y=E{Y}^2-D(Y)<E{Y}^2$ ，所以有

$$|E(X_n-X)|\le \sqrt{E|X_n-X{|}^2}$$

左右两边取极限，右边根据均方收敛得到0，所以${\lim }_{n\to \infty }|E(X_n-X)|=0$，${\lim }_{n\to \infty }E{X}_n=EX=E({\text{l.i.m.}}_{n\to \infty }{X}_n)$

定理3.2：若均方收敛，$X_n$依概率收敛于X
由切比雪夫不等式

$$\forall \epsilon >0,P(|X_n-X|>\epsilon )\le \frac{E|X_n-X{|}^2-E^2|X_n-X|}{{\epsilon }^2}$$

左右取极限，由均方收敛和定理3.1可得右边为0，所以${\lim }_{n\to \infty }P(|X_n-X|>\epsilon )\to 0$，$X_n$ 依概率收敛于$X$

定义3.2：随机过程的均方收敛
随机过程 $\{X(t),t\in T\}$ 满足，$t_0,t_0+\Delta t\in T$时

$$\underset{\Delta t\to 0}{\lim }E|X(t_0+\Delta t)-X(t_0){|}^2=0$$

即t取极限时均方收敛

$${\text{l.i.m.}}_{\Delta t\to 0}X(t_0+\Delta t)=X(t_0)$$

称$X(t)$在$t_0$处均方连续，进一步地，在每个$t$都均方连续，则在$T$上均方连续
根据定理3.2，均方收敛则概率收敛，$\Delta t\to 0,\forall \epsilon ,\forall \eta ,P(|X(t_0+\Delta t)-X(t_0)|>\epsilon )<\eta$，当时间给出微小扰动时，扰动后的状态和扰动前有差别的概率趋近于0，体现了随机过程连续性的统计物理意义

定义3.3：定义随机过程极限
若均方极限

$${\text{l.i.m.}}_{\Delta t\to 0}\frac{X(t_0+\Delta t)-X(t_0)}{\Delta t}$$

存在，则称该极限为$X(t)$在$t_0$处的均方导数，记作$X^{\prime }(t_0)\text{ 或 }\frac{dX(t)}{dt}{|}_{t=t_0}$，也称均方可导
每一处可导则在T上均方可导，记作 $X^{\prime }(t)\text{ 或 }\frac{dX(t)}{dt}$，也是一个随机过程
均方导数和普通导数有相似的性质

定义3.4：定义积分
设随机过程 $\{X(t),t\in T=[a,b]\}$，$f(t)$为任意普通函数。将$[a,b]$分为n个子区间$[t_k,t_{k+1}],k=0,\mathrm{1...}n$
记

$$\Delta t=\max (t_k-t_{k-1})=\max \Delta t_k,k\in [1,n]$$ $$Y_n=\sum _{k=1}^{n}f({\xi }_k)X({\xi }_k)(t_k-t_{k-1})=\sum _{k=1}^{n}f({\xi }_k)X({\xi }_k)\Delta t_k{\xi }_k\in [t_{k-1},t_k]$$

如果当$\Delta t$ 趋近于0时，$Y_n$ 能均方收敛于$Y$，称$f(t)X(t)$在T上均方可积，称$Y$为$f(t)X(t)$在T上的均方积分

$$\begin{array}{rl}Y& ={\int }_a^{b}f(t)X(t)dt\\ & ={\text{l.i.m.}}_{\Delta t\to 0}\sum _{k=1}^{n}f({\xi }_k)X({\xi }_k)\Delta t_k{\xi }_k\in [t_{k-1},t_k]\end{array}$$

定理3.3：若$X(t)$ 在$[a,b]$上均方可积，则

$${\left[{\int }_a^{t}X(s)ds\right]}^{\prime }=X(t)$$

均方积分满足一些基本定理
牛顿-莱布尼兹公式 ($X(t)$均方可导，$X^{\prime }(t)$ 均方连续)

$${\int }_a^b{X}^{\prime }(t)dt=X(b)-X(a)$$

期望计算

$$E\left[{\int }_a^{b}X(t)dt\right]={\int }_a^{b}E[X(t)]dt$$

定义3.5：n阶线性随机微分方程
设随机过程 $X(t),t\in T$ 与$Y(t),t\in T$ 为随机过程，$Y(t)$ 的 n 阶均方方导数 $Y^{(n)}(t)$ 存在，$a_k(1\le k\le n)$ 为随机变量或常数，则称：

$$a_n{Y}^{(n)}(t)+a_{n-1}{Y}^{(n-1)}(t)+\cdots +a_1{Y}^{\prime }(t)+a_{0}Y(t)=X(t)(1.9)$$

一阶线性微分方程写为

$$dY=f(X,Y)dt$$

布朗运动

一条直线上，对称的随机游动，形式化表示为：经过$\Delta t$时间，随机地向左或向右移动$\Delta x$ 个单位，向左或向右概率均为1/2，且每次移动互相独立，记为

$$X_i=\{\begin{array}{ll}1,& \text{质点第i次向右移动}\\ -1,& \text{质点第i次向左移动}\end{array}$$

令$X(t)$ 表示 $t$ 时刻质点的位置，有$X(t)=\Delta x(X_1+X_2+...X_{[\frac{t}{\Delta t}]})$，其中 $[x]$ 表示不超过 $x$ 的最大整数
我们希望得到 $X(t)$ 分布，有 $E{X}_i=0,D{X}_i=E{X}_i^2-E^2{X}_i=1$，所以 $E[X(t)]=0,D[X(t)]=\left[\frac{t}{\Delta t}\right](\Delta x{)}^2$
说，如果考虑 $\Delta t\to 0$ 的情景，$\Delta x\to 0$，为了令 $D[X(t)]$ 收敛且数值稳定，一般令 $\Delta x$ 是 $\sqrt{\Delta t}$ 的同阶无穷小，即 $\Delta x=c\sqrt{\Delta t}$
此时 $D[X(t)]={\lim }_{\Delta t\to 0}\left[\frac{t}{\Delta t}\right](\Delta x{)}^2={\lim }_{\Delta t\to 0}\left[\frac{t}{\Delta t}\right]c^2\Delta t=c^{2}t.$
由中心极限定理可得

$$\underset{\Delta t\to 0}{\lim }P\left\{\frac{{\sum }_{i=0}^{\left[\frac{t}{\Delta t}\right]}\Delta x{X}_i-0}{\sqrt{c^{2}t}}\le x\right\}=\Phi (x)$$ $$\underset{\Delta t\to 0}{\lim }P\left\{\frac{X(t)}{\sqrt{c^{2}t}}\le x\right\}=\Phi (x)=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^x{e}^{-\frac{u^2}{2}}du$$

所以 $X(t)$ 趋于正态分布，即$\Delta t\to 0$，$X(t)\sim N(0,c^{2}t)$

基于此，定义对于随机过程 $X(t),t\ge 0$，如果

• $X(t)$ 是独立增量过程
• $\forall s,t>0,X(s+t)-X(s)\sim N(0,c^{2}t);$
  则称该随机过程是布朗运动，记为 $B(t)$ (或维纳过程， $W(t)$)
  若 $c=1$，称标准布朗运动 $W(t)\sim N(0,t)$

布朗运动是基于随机游走定义的，(时间间隔非常小时)服从正态分布，方差为 $c^{2}t$，时间越长位置越不好预测
后续出现的布朗运动应该都是标准布朗运动

Ito积分 和 扩散过程

我们关心布朗运动两个时间节点移动的曲线长度。在随机过程中，可以采用 有界变差 来描述随机运动路径长度
将时间区间$[0,T]$进行划分，$0=t_0<t_1<...<t_n=T$，即将两个时间点的区间划分为多个时间步，每步的矢量距离为 $W(t_{i+1}-W_{t_i})$，所以曲线长度可近似为 $|W(t_{i+1}-W_{t_i})|$
总距离近似为

$$\sum _{i=0}^{n-1}|W(t_{i+1})-W(t_i)|$$

令 $\delta ={\max }_{0\le i\le n-1}\{t_{i+1}-t_i\}$，布朗运动 $W(t),t\ge 0$的有界变差 $WV(T)$ 为

$$WV(T)={\text{l.i.m.}}_{\delta \to 0}\sum _{i=0}^{n-1}|W(t_{i+1})-W(t_i)|$$

但是布朗运动的有界变差并不存在
定义二阶变差

$$[W,W]([0,T])={\text{l.i.m.}}_{\delta \to 0}\sum _{i=0}^{n-1}|W(t_{i+1})-W(t_i){|}^2$$

布朗运动的二阶变差 $[W,W]([0,T])=T$

DFW没有搞懂推导出二阶变差和它的推论目的是什么，暂时跳过

就结论而言，设 $\{X(t),t\in [0,T]\}$ 为随机过程，若积分

$$I={\int }_0^{T}g(X(t),t)dW$$ $$\sum _{t=0}^{n-1}g(X(t_i),t_i)[W(t_{i+1})-W(t_i)]\stackrel{m.s.}{⟶}I$$

称积分 $I$ 为 Ito积分
进一步的 形如

$$X(T)-X(0)={\int }_0^{T}f(X(t),t)dt+{\int }_0^{T}g(X(t),t)dW$$

称为积分形式Ito随机微分方程

$$dX(t)=f(X(t),t)dt+g(X(t),t)dW$$

称为微分形式Ito随机微分方程或Ito过程或漂移布朗运动或扩散方程
扩散方程中，$f(X(t),t)$ (与$dX$构成一阶均方微分方程)一项给出了下一时刻$X(t+\Delta t)$与当前时刻$X(t)$的确定性关系，$g(X(t),t)dW$中由于布朗运动，该项相当于噪声项，引入了随机性

Ito积分有一些性质
如期望为0

$$E\left[{\int }_s^{T}g(X(t),t)dW\right]=0$$

Ito引理(二元泰勒展开，高阶项可证为0)

$$df(t,X_t)=\frac{\partial f(t,X_t)}{\partial t}dt+\frac{\partial f(t,X_t)}{\partial X_t}d{X}_t+\frac{1}{2}\frac{{\partial }^{2}f(t,X_t)}{(\partial X_t{)}^2}(d{X}_t{)}^2$$

Diffusion

回忆diffusion的加噪过程，$x_t=\sqrt{a_t}{x}_{t-1}+\sqrt{1-a_t}{ϵ}_t$
这样的加噪过程是离散的，为了应用到SDE中先考虑连续化。在每两个时间步中加入中间操作，不断反复可得连续过程

首先简化问题，考虑加噪过程是线性的
对前半项有 $(\sqrt{{\alpha }_t}-1)x_{t-1}dt$(斜率)，后半项对标准正态分布采样，本身是离散的比较难连续化。我们已经知道布朗运动$W(1)\sim N(0,1)$，所以可以直接用连续的布朗运动来替换

$${\epsilon }_{t+dt}-{\epsilon }_t=W(t+dt)-W(t)=dW\sim N(0,dt)$$

整个过程为

$$dx=(\sqrt{{\alpha }_t}-1)x_{t-1}dt+\sqrt{1-{\alpha }_t}dW$$

这里是简化后的随机微分方程，更通用的可以将$\sqrt{{\alpha }_t}-1)x_{t-1},\sqrt{1-{\alpha }_t}$扩展为 $f(x,t),g(t)$，则得到了常见的一般形式的微分方程

$$dx=f(x,t)dt+g(t)dW$$

顺带一提，宋飏博士在score based 论文中提出的扩散过程SDE保留了原有的前向关系式(即具体的加噪过程)，称 VP过程 Variance Preserving

每个SDE都对应一个逆向过程，在生成扩散模型漫谈（五）：一般框架之SDE篇 - 科学空间|Scientific Spaces中对扩散过程逆向SDE有一个简单的证明
扩散模型的逆向SDE为

$$dx=[f(x,t)-g^2(t){\nabla }_x\log p_t(x)]dt+g(t)dW$$

直接求解过于困难，我们可以通过采样$x_T$，离散化来求解，这种方法称为Euler-Maruyama Method

$$x_{t+\Delta t}-x_t=[f(x_{t+\Delta t},t_{t+\Delta t})-g^2(t_{t+\Delta t}){\nabla }_{x_{t+\Delta t}}\log p_{t+\Delta t}(x_{t+\Delta t})]\Delta t+g(t_{t+\Delta t})\sqrt{\Delta t}{\epsilon }_{t+\Delta t}$$

我们从标准正态分布采样 $x_T$，通过上式不断求解。
但是实际上 ${\nabla }_x\log p_t(x)$ 是不知道的，也就是score function未知，我们需要通过模型拟合，使用得分匹配算法

$$\mathcal{L}={\mathbb{E}}_{t\sim U[0,T]}\left[\lambda (t)\int p_t(x)||s_{\theta }(x,t)-{\nabla }_x\log p_t(x)|{|}^{2}dx\right]$$

等价于引入$x_0$的形式

$$\mathcal{L}={\mathbb{E}}_{t\sim U[0,T]}\left[\lambda (t)\int p_t(x,x_0)||s_{\theta }(x,t)-{\nabla }_x\log p_t(x\mid x_0)|{|}^{2}dx\right]$$

最后得到采样方法

$$x_{t+\Delta t}-x_t=[f(x_{t+\Delta t},t_{t+\Delta t})-g^2(t_{t+\Delta t})s(x_{t+\Delta t},t+\Delta t)]\Delta t+g(t_{t+\Delta t})\sqrt{\Delta t}{\epsilon }_{t+\Delta t}$$

此处博客提到了这样的采样方法要比基于MCMC的朗之万采样SMLD模型效率更高，前者两个时间步间进行一次采样(调用一次score function)，后者需要多次调用

另外的，基于朗之万方程采样的模型可以称为 VE(Variance Exploding) 模型
可以通过其前向过程对应的逆向SDE推导出朗之万方程

Notes

VP 和 VE

DDPM被称为VP(Variance Preserving)，即方差紧缩。这是因为DDPM的前向过程为

$$x_T=\sqrt{{\bar{a}}_T}{x}_0+\sqrt{1-{\bar{a}}_T}ϵ$$

有一个对$x_0$的缩放(通过很小的${\sqrt{\bar{a}}}_t$来压制$x_0$)，并通过方差并不大的$\sqrt{1-{\bar{a}}_T}$来进行加噪
而NCSN被称为 VE(Variance Exploding)，即方差爆炸。它的前向是

$$x_T=x_0+{\sigma }_Tϵ$$

它没有缩放$x_0$，是通过方差很大的${\sigma }_Tϵ$ 来压制$x_0$

SDE框架统一了NCSN和DDPM，可证二者实际上完全等价

$$\frac{x_t}{\sqrt{1+{\sigma }_t^2}}=\frac{x_0}{\sqrt{1+{\sigma }_t^2}}+\frac{{\sigma }_t}{\sqrt{1+{\sigma }_t^2}}ϵ$$ $$x_t=\frac{x_t}{\sqrt{1+{\sigma }_t^2}}$$ $$\sqrt{{\bar{\alpha }}_t}=\frac{1}{\sqrt{1+{\sigma }_t^2}}$$ $$x_t=\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}ϵ$$

SDE 最终是通过score function来进行生成过程，对于DDPM来说，DDPM没有训练过预测score，可进一步证明

$${ϵ}_{\theta }(x_t,t)=\frac{x_t-\sqrt{{\bar{\alpha }}_t}{x}_0}{\sqrt{1-{\bar{\alpha }}_t}}$$ $$s_{\theta }(x_t,t)={\nabla }_{x_t}\log (x_t)=-\frac{x_t-\sqrt{{\bar{\alpha }}_t}{x}_0}{1-{\bar{\alpha }}_t}$$ $${\nabla }_{x_t}\log (x_t)=s_{\theta }(x_t,t)=-\frac{1}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }(x_t,t)$$

即实际上二者只是方向不同，可以直接将DDPM迁移到score based的采样方法上

PF-ODE

PF-ODE(Probability flow ODE)
概率流常微分方程

DDIM不考虑前向传播过程$p(x_t|x_{t-1})$，直接考虑边际分布$p(x_t|x_0)$，加速了采样。那SDE有没有类似的做法呢

找到SDE对应的边际分布的方法就是 Fokker-Planck 方程
博客Diffusion学习笔记（四）——概率流ODE（Probability flow ODE）的推导略显复杂，此处记录一下苏神的推导生成扩散模型漫谈（六）：一般框架之ODE篇 - 科学空间|Scientific Spaces

首先改变一下记号方便参照原博客
回顾一下SDE的前向

$$dx=f_t(x)dt+g_{t}dw$$ $$x_{t+\Delta t}-x_t=f_t(x_t)\Delta t+g_t\sqrt{\Delta t}{ϵ}_t$$

我们希望直接得到SDE对应的边际分布而不是通过逐步考虑随机性来进行采样

我的理解是，每个SDE都对应一个边际分布，之所以有 “分布” 是因为$W(t)$引入了随机性，我们希望像DDIM一样直接得到边际分布来得到一个更泛化的形式

我们可以引入Dirac函数

$$p(x)=\int \delta (x-y)p(y)dy={\mathbb{E}}_y[\delta (x-y)]$$

Dirac函数可以通过求期望来得到分布
我们希望得到描述边际分布的微分方程，或者说得到$p_t(x)$，则通过Dirac函数问题转化为对$\delta (x-x_{t+\Delta t})$求期望(这里得到的实际上是$p_{t+\Delta t}$，需要去取极限消去$\Delta t$)

另外，Dirac函数还有如下性质

$$p(x)f(x)=\int \delta (x-y)p(y)f(y)dy={\mathbb{E}}_y[\delta (x-y)f(y)]$$

两边求偏导

$${\nabla }_x[p(x)f(x)]={\mathbb{E}}_y[{\nabla }_x\delta (x-y)f(y)]={\mathbb{E}}_y[f(y){\nabla }_x\delta (x-y)]$$

接下来推导F-P方程
代入得到 $\delta (x-x_{t+\Delta t})$ 的具体形式

$$\begin{array}{rl}\delta (x-x_{t+\Delta t})& =\delta (x-x_t-f_t(x_t)\Delta t-g_t\sqrt{\Delta t}ϵ)\\ & \approx \delta (x-x_t)-(f_t(x_t)\Delta t+g_t\sqrt{\Delta t}ϵ)\cdot {\nabla }_x\delta (x-x_t)+\frac{1}{2}(g_t\sqrt{\Delta t}ϵ\cdot {\nabla }_x{)}^2\delta (x-x_t)\end{array}$$

泰勒展开

求期望

$$\begin{array}{rl}{p}_{t+\Delta t}(x)& ={\mathbb{E}}_{x_{t+\Delta t}}[\delta (x-x_{t+\Delta t})]\\ & \approx {\mathbb{E}}_{x_t,ϵ}\left[\delta (x-x_t)-(f_t(x_t)\Delta t+g_t\sqrt{\Delta t}ϵ)\cdot {\nabla }_x\delta (x-x_t)+\frac{1}{2}(g_t\sqrt{\Delta t}ϵ\cdot {\nabla }_x{)}^2\delta (x-x_t)\right]\\ & ={\mathbb{E}}_{x_t}\left[\delta (x-x_t)-f_t(x_t)\Delta t\cdot {\nabla }_x\delta (x-x_t)+\frac{1}{2}{g}_t^2\Delta t{\nabla }_x\cdot {\nabla }_x\delta (x-x_t)\right]\\ & =p(x)-{\nabla }_x\cdot [f_t(x_t)\Delta tp(x)]+\frac{1}{2}{g}_t^2\Delta t{\nabla }_x\cdot {\nabla }_x{p}_t(x)\end{array}$$

左右两边除以$\Delta t$，取极限得到

$$\frac{\partial }{\partial t}{p}_t(x)=-{\nabla }_x\cdot [f_t(x)p_t(x)]+\frac{1}{2}{g}_t^2{\nabla }_x\cdot {\nabla }_x{p}_t(x)$$

对于任意的${\sigma }_t$，如果满足 ${\sigma }_t^2\le g_t^2$ 有以下等价变换

$$\begin{array}{rl}\frac{\partial }{\partial t}{p}_t(x)& =-{\nabla }_x\cdot \left[f_t(x)p_t(x)-\frac{1}{2}(g_t^2-{\sigma }_t^2){\nabla }_x{p}_t(x)\right]+\frac{1}{2}{\sigma }_t^2{\nabla }_x\cdot {\nabla }_x{p}_t(x)\\ & =-{\nabla }_x\cdot \left[\left(f_t(x)-\frac{1}{2}(g_t^2-{\sigma }_t^2){\nabla }_x\log p_t(x)\right)p_t(x)\right]+\frac{1}{2}{\sigma }_t^2{\nabla }_x\cdot {\nabla }_x{p}_t(x)\end{array}$$

这个变换相当于把$f(x)$换成 $\left(f_t(x)-\frac{1}{2}(g_t^2-{\sigma }_t^2){\nabla }_x\log p_t(x)\right)$，将$g$换成$\sigma$，二者完全等价
这个新的F-P方程对应于SDE

$$dx=\left(f_t(x)-\frac{1}{2}(g_t^2-{\sigma }_t^2){\nabla }_x\log p_t(x)\right)dt+{\sigma }_{t}dw$$

我们再对比两个SDE

$$dx=f_t(x)dt+g_{t}dw$$

两个F-P方程完全等价，所以两个SDE对应的边际分布是相同的，也就是存在多条不同的路径/前向过程(通过不同的方差$\sigma$)，我们就得到了一个DDIM的升级版

此时的逆向SDE为

$$dx=\left(f_t(x)-\frac{1}{2}(g_t^2+{\sigma }_t^2){\nabla }_x\log p_t(x)\right)dt+{\sigma }_{t}dw$$

将$\sigma$置为0，我们得到ODE

$$dx=\left(f_t(x)-\frac{1}{2}{g}_t^2{\nabla }_x\log p_t(x)\right)dt$$

称为概率流ODE，中间的${\nabla }_x\log p_t(x)$ 未知，所以需要用模型拟合，也会对应一个神经ODE
代入可以得到其逆向和前向是一致的，我们得到了一个确定性的可逆的过程
这和flow matching一致，这样的做法允许我们进行精确的计算，又由于可逆性允许进行图像编辑等
另外的，对ODE的加速求解方法研究较多，我们也可以使用一些ODE求解方法来进行加速

当$f_t(x)$为线性时($f_{t}x$)，得到DDIM

References

• [2006.11239] Denoising Diffusion Probabilistic Models
• [2010.02502] Denoising Diffusion Implicit Models
• [2011.13456] Score-Based Generative Modeling through Stochastic Differential Equations
• Diffusion学习笔记（三）——随机微分方程（SDE）
• Diffusion学习笔记（四）——概率流ODE（Probability flow ODE）
• 生成扩散模型漫谈（三）：DDPM = 贝叶斯 + 去噪 - 科学空间|Scientific Spaces
• 生成扩散模型漫谈（四）：DDIM = 高观点DDPM - 科学空间|Scientific Spaces
• 生成扩散模型漫谈（五）：一般框架之SDE篇 - 科学空间|Scientific Spaces
• 扩散模型之DDIM