Diffusion

What are Diffusion Models

GAN models are known for potentially unstable training and less diversity in generation due to their adversarial training nature. VAE relies on a surrogate loss. Flow models have to use specialized architectures to construct reversible transform.
from What are Diffusion Models? | Lil’Log 感觉是精辟的总结

Notes

Some background needed

Markov chain

马尔科夫链(markov chains)是一个数学模型，根据某些概率规则从一个状态转移到另一个状态，它的特点是马尔可夫性质(markov property)，转化(transition)到未来任意状态的概率只依赖于当前的状态，与过去的状态无关，称 无记忆性 (memorylessness) 即，马尔可夫系统不保存过去信息

non-equilibrium thermodynamics

非平衡态热力学是热力学的一个分支，研究系统在远离平衡态时的行为
扩散模型中正向扩散近似于非平衡态热力学中的熵增过程，反向扩散近似于熵减的过程

扩散模型定义了一个不断增加随机噪声的马尔可夫链，模型学习如何reverse the diffusion process来从噪声中构造想要的数据
扩散模型的训练过程是固定的，在高维的空间(与原数据一致)中训练(而没降维)

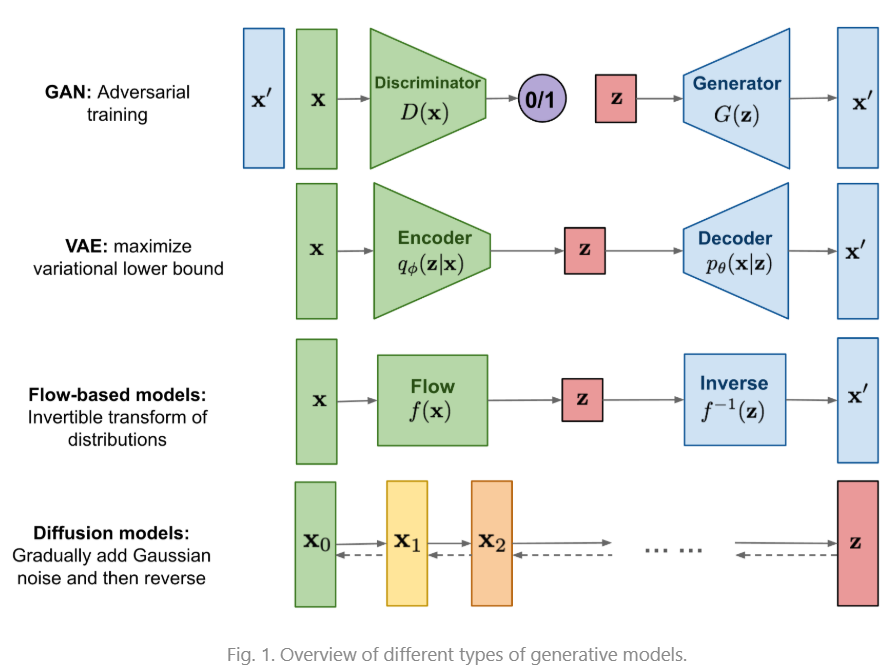
Forward diffusion process 前向过程

逐步增加高斯噪声的马尔可夫链

给定样本x，逐步增加高斯噪声，总共执行T步，产生一系列的noisy sample $x_1,x_2,...x_T$。Step size受varianve schedule ${\beta }_t\in (0,1)$
${\beta }_t$ 一般随着步数增加，直到最后一步，样本趋近于纯噪声(标准正态分布)

数学表达式为

$$q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})=\mathcal{N}({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I})q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)=\prod _{t=1}^{T}q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})$$

• 第一个式子表明单步转移概率分布(转移到$x_t$状态的概率)是服从 均值为$\sqrt{1-{\beta }_t}$ 和 方差为${\beta }_{t}I$的正态分布
• 第二个式子即时马尔可夫链的基本形式

这样的定义我们可以sample任意时刻的 $x$ (reparameterization trick)

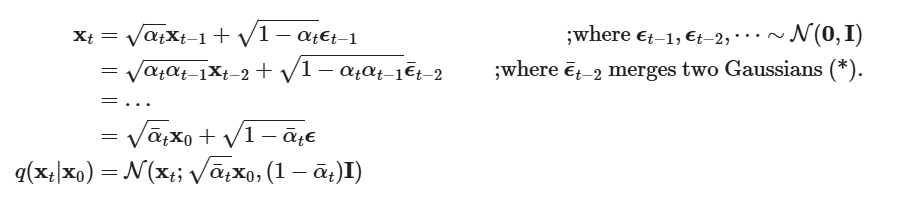
其中 ${\alpha }_t=1-{\beta }_t\mathrm{and}{\bar{\alpha }}_t={\prod }_{i=1}^t{\alpha }_i$
${\beta }_i$ 逐渐增大，$\bar{\alpha }$ 逐渐减小

为什么能这么算呢
实际上动笔硬算就行
两个高斯分布相加，得到 $\mathcal{N}(0,({\sigma }_1^2+{\sigma }_2^2)\mathbf{I}).$
计算标准差为 $\sqrt{(1-{\alpha }_t)+{\alpha }_t(1-{\alpha }_{t-1})}=\sqrt{1-{\alpha }_t{\alpha }_{t-1}}.$ 注意此时标准差第二个有展开后得到的加权

Connection with stochastic gradient Langevin dynamics(朗之万动力学)

stochastic gradient Langevin dynamics can produce samples from a probability density $p(x)$ using only the gradients ${\nabla }_{\mathbf{x}}\log p(\mathbf{x})$ in a Markov chain of updates

$${\mathbf{x}}_t={\mathbf{x}}_{t-1}+\frac{\delta }{2}{\nabla }_{\mathbf{x}}\log p({\mathbf{x}}_{t-1})+\sqrt{\delta }{ϵ}_t,\mathrm{where}{ϵ}_t\sim \mathcal{N}(0,\mathbf{I})$$

其中 $\delta$ 是 step size，当 $T\to \infty ,ϵ\to 0$的时候，$x_T$ 等于真实的概率密度 $p(x)$

这种梯度更新法加入了Gaussian noise避免了陷入local minima中

Note

为什么出现了这个？

朗之万动力学是一种从复杂分布中采样的方法，通过确定性(梯度)和随机性(噪声)，x 逐渐趋近于目标分布 $p(x)$
Diffusion的反向过程可以看成是一种相近的形式(NCSN角度)
这一角度，Diffusion 可以被描述为一种 score-based 模型

Reverse diffusion process

如果我们能reverse forward的过程(从$q(x_{t-1}|x_t)$中抽样)，我们就能从高斯噪声中重构图像。如果${\beta }_t$ 足够小，$q(x_{t-1}|x_t)$仍然是高斯分布。
如果 $q(x_{t-1}|x_t)$ 仍然是高斯分布，它应满足

$$q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)=\mathcal{N}({\mathbf{x}}_{t-1};\mathbf{\mu }({\mathbf{x}}_t,t),\mathbf{\Sigma }({\mathbf{x}}_t,t))$$

假若数据皆可访问，我们能通过上面的trick直接得到分布
但是现实数据是不能全部访问的，所以我们不能直接得到$q(x_{t-1}|x_t)$。因此我们需要有一个模型 $p_{\theta }$ 来预测这个均值与方差
数学表达式如下

$$p_{\theta }({\mathbf{x}}_{0:T})=p({\mathbf{x}}_T)\prod _{t=1}^T{p}_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)=\mathcal{N}({\mathbf{x}}_{t-1};{\mu }_{\theta }({\mathbf{x}}_t,t),{\mathbf{\Sigma }}_{\theta }({\mathbf{x}}_t,t))$$

如果给定 $x_0$ (conditioned $x_0$)，$q(x_{t-1}|x_t,x_0)$ 是比较容易处理的

$$q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)=\mathcal{N}({\mathbf{x}}_{t-1};\tilde{\mu }({\mathbf{x}}_t,{\mathbf{x}}_0),{\tilde{\beta }}_t\mathbf{I})$$

有如下数学推导

根据Bayes’ rule 有

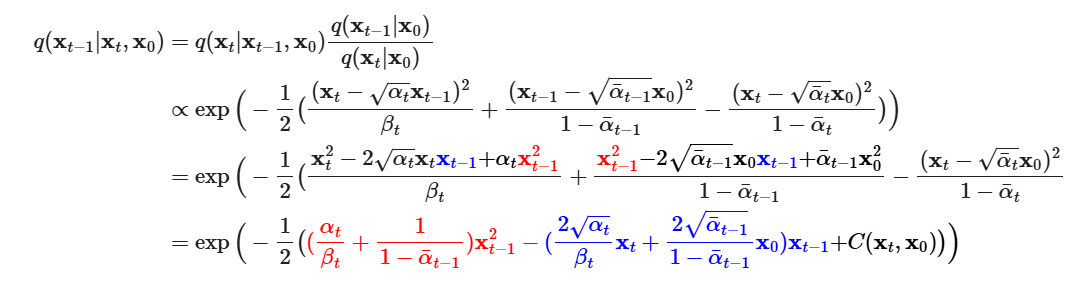
Notes

about Bayes’ rule

贝叶斯公式

$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

$P(A)$ 称为A的先验概率，$P(B)$为B的先验概率，$P(A|B)$是后验概率，$P(B|A)$称为A和B的似然性
则贝叶斯公式描述为

$$后验概率=(先验概率\times 似然性)/标准化常数$$

贝叶斯公式可扩展到两个以上的变量

$$P(A|B,C)=\frac{P(A)P(B|A)P(C|A,B)}{P(B)P(C|B)}$$

补一点说明
根据两个变量的贝叶斯公式，A为 $x_{t-1}$，B为 $x_0$，C为 $x_t$ ，将 $P(A)P(B|A)/P(B)$ 转为条后验概率 $P(A|B)$ 则可以得到一开始的式子
再往后的推导基于高斯分布，具体的不是很懂，目标是求出当前高斯分布 $q(x_{t-1}|x_t,x_0)$ 的均值与方差

根据高斯分布的形式，忽视 $C(x_t,x_0)$(与 $x_{t-1}$ 无关，影响不大) 化简二次项得到

$${\tilde{\beta }}_t=1/(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})=1/(\frac{{\alpha }_t-{\bar{\alpha }}_t+{\beta }_t}{{\beta }_t(1-{\bar{\alpha }}_{t-1})})=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t$$ $$\begin{array}{rl}{\tilde{\mu }}_t({\mathbf{x}}_t,{\mathbf{x}}_0)& =(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0)/(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})\\ & =(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0)\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t\\ & =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\bar{\beta }}_t}{1-{\bar{\alpha }}_t}{\mathbf{x}}_0\end{array}$$

实际上，DDPM的做法并不在意方差 $\tilde{\beta }$，DDPM 固定方差（相比于学习方差来尝试优化效果） 所以重点在 ${\tilde{\mu }}_t({\mathbf{x}}_t,{\mathbf{x}}_0)$
根据前面的trick，有 ${\mathbf{x}}_0=\frac{1}{\sqrt{{\bar{\alpha }}_t}}({\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_t)$
则

$$\begin{array}{l}{\tilde{\mu }}_t=\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}\frac{1}{\sqrt{{\bar{\alpha }}_t}}({\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_t)\\ =\frac{1}{\sqrt{{\alpha }_t}}\left(x_t-\frac{1-a_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_t\right)\end{array}$$

我们希望模型预测出分布的均值，我们需要让模型预测结果接近 ${\tilde{\mu }}_t({\mathbf{x}}_t,{\mathbf{x}}_0)$

到这里我们可以跳步，因为 ${\tilde{\mu }}_t$ 的各个变量，只有 $ϵ$ 是非确定的，其余都是模型预测前给定的，所以我们只要让模型预测这个 $ϵ$ ，即噪声就行。至于如何计算损失，随便引入一个MSE直觉上是合理的，DDPM的结果也是如此。
只是我们可能需要一个更make sense 的推导，来选择一个符合目标( $\mathrm{argmax}log{p}_{\theta }(x)$ )的损失

回到目标上，根据ELBO技巧，有

$$\begin{array}{rl}{L}_{CE}& =-{\mathbb{E}}_{q(x_0)}\log p_{\theta }(x_0)\\ & =-{\mathbb{E}}_{q(x_0)}\log \left(\int p_{\theta }(x_{0:T})d{x}_{1:T}\right)\\ & =-{\mathbb{E}}_{q(x_0)}\log \left(\int q(x_{1:T}|x_0)\frac{p_{\theta }(x_{0:T})}{q(x_{1:T}|x_0)}d{x}_{1:T}\right)\\ & =-{\mathbb{E}}_{q(x_0)}\log \left({\mathbb{E}}_{q(x_{1:T}|x_0)}\left[\frac{p_{\theta }(x_{0:T})}{q(x_{1:T}|x_0)}\right]\right)\\ & \le -{\mathbb{E}}_{q(x_{0:T})}\log \frac{p_{\theta }(x_{0:T})}{q(x_{1:T}|x_0)}\\ & ={\mathbb{E}}_{q(x_{0:T})}\left[\log \frac{q(x_{1:T}|x_0)}{p_{\theta }(x_{0:T})}\right]=L_{VLB}\end{array}$$

我们得到VLB，然后将VLB的各项推导成tacklable的形式
有

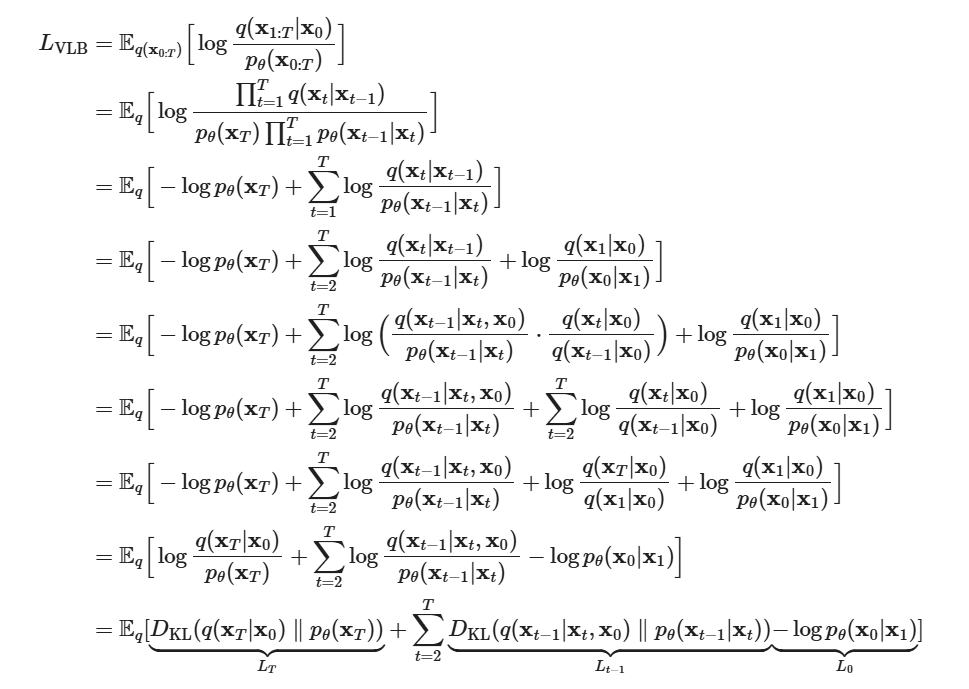
为了简单描述，将各项重写为

$$\begin{array}{c}{L}_{\mathrm{VLB}}=L_T+L_{T-1}+\cdots +L_0\\ \mathrm{where}{L}_T=D_{\mathrm{KL}}(q({\mathbf{x}}_T|{\mathbf{x}}_0)\parallel p_{\theta }({\mathbf{x}}_T))\\ L_t=D_{\mathrm{KL}}(q({\mathbf{x}}_t|{\mathbf{x}}_{t+1},{\mathbf{x}}_0)\parallel p_{\theta }({\mathbf{x}}_t|{\mathbf{x}}_{t+1}))\mathrm{for}1\le t\le T-1\\ L_0=-\log p_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)\end{array}$$

可以看到 $L_T$ 是固定值($q(x_T|x_0)$ 是正向加噪过程，固定；而 $p_{\theta }(x_T)$ 是反向的起点，即得到Gaussian noise $x_T$ 的分布，也就是一个标准正态分布)，$L_0$ 在原论文中使用 seperate discrete decoder 处理

我们重点关注 $L_t$
$L_t$ 所有项都是两个分布的KL 散度，其中 $q(x_t|x_{t+1},x_0)$ 是我们上文推导得到的反向真实分布，而 $p_{\theta }(x_t|x_{t+1})$ 是模型预测的反向过程
对于 $q(x_t|x_{t+1},x_0)$ 有分布

$$q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)=\mathcal{N}({\mathbf{x}}_{t-1};\frac{1}{\sqrt{{\alpha }_t}}\left(x_t-\frac{1-a_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_t\right),{\tilde{\beta }}_t\mathbf{I})$$

对于 $p_{\theta }(x_t|x_{t+1})$ 有分布

$${\mathbf{x}}_{t-1}=\mathcal{N}({\mathbf{x}}_{t-1};\frac{1}{\sqrt{{\alpha }_t}}({\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }({\mathbf{x}}_t,t)),{\Sigma }_{\theta }({\mathbf{x}}_t,t))$$

我们可以得到

$$\begin{array}{rl}{L}_t& ={\mathbb{E}}_{x_0,ϵ}\left[\frac{1}{2||{\Sigma }_{\theta }(x_t,t)|{|}^2}||{\tilde{\mathbf{\mu }}}_{\theta }({\mathbf{x}}_t,t)-\mathbf{\mu }({\mathbf{x}}_t,t)|{|}^2\right]\\ & ={\mathbb{E}}_{x_0,ϵ}\left[\frac{1}{2||{\Sigma }_{\theta }|{|}^2}||\frac{1}{\sqrt{{\alpha }_t}}\left({\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}\mathbf{ϵ}\right)-\frac{1}{\sqrt{{\alpha }_t}}\left({\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)\right)|{|}^2\right]\\ & ={\mathbb{E}}_{x_0,ϵ}\left[\frac{(1-{\alpha }_t{)}^2}{2{\alpha }_t(1-{\bar{\alpha }}_t)||{\Sigma }_{\theta }|{|}^2}||\mathbf{ϵ}-{\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)|{|}^2\right]\\ & ={\mathbb{E}}_{x_0,ϵ}\left[\frac{(1-{\alpha }_t{)}^2}{2{\alpha }_t(1-{\bar{\alpha }}_t)||{\Sigma }_{\theta }|{|}^2}||\mathbf{ϵ}-{\mathbf{ϵ}}_{\theta }(\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}\mathbf{ϵ},t)|{|}^2\right]\end{array}$$

复杂的推导不是很会，这里应是将两个分布的方差当成是一致的，则KL 散度等价于两个均值的加权平方差(直觉理解确实)

DDPM 在训练的时候简化了这个损失，改成

$$\begin{array}{rl}{L}_t^{\mathrm{simple}}& ={\mathbb{E}}_{t\sim [1,T],{\mathbf{x}}_0,{ϵ}_t}[\Vert {\mathbf{ϵ}}_t-{\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t){\Vert }^2]\\ & ={\mathbb{E}}_{t\sim [1,T],{\mathbf{x}}_0,{ϵ}_t}[\Vert {\mathbf{ϵ}}_t-{\mathbf{ϵ}}_{\theta }(\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}{\mathbf{ϵ}}_t,t){\Vert }^2]\end{array}$$

最终的损失化简为

$$L_{simple}=L_t^{simple}+C$$

也就是训练伪代码中

这里实际上应该注意到，我们原本应该计算所有$t$来构成目标函数，但是我们没有求所有 t 的KL 散度作为损失，而是一个 $L_t$
训练过程可以被理解为，使用蒙特卡洛来估计 原目标函数的期望

生成部分的伪代码也可以理解为构造了 $x_{t-1}$ 的分布

Connection with noise-conditioned score networks(NCSN)

知识匮乏，看个大概
有一种score-based generative model method，基于 Langevin dynamics，使用 数据分布的gradients从分布中采样。这个gradients没能真实得到，通过模型来进行估计。
即

$${\mathbf{s}}_{\theta }(\mathbf{x})\approx {\nabla }_{\mathbf{x}}\log q(\mathbf{x}).$$

其中$s_{\theta }$ 是score network，梯度为 score 的定义
根据 manifold hypothesis，尽管数据看上去是高维的，大多数数据都集中在低维的manifold中。为了在高维上scalable，有以下两种方法，一种是额外增加噪声(denoising score matching)，一种是随机投影(sliced score matching)

其中denoising score matching的做法是 给 $q(\tilde{x}|x)$ 增加一个 预先定义的噪声，通过score matching 来拟合 $q(\tilde{x})$

在 Diffusion 的语境下

$$q({\mathbf{x}}_t|{\mathbf{x}}_0)\sim \mathcal{N}(\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0,(1-{\bar{\alpha }}_t)\mathbf{I})$$ $${\mathbf{s}}_{\theta }({\mathbf{x}}_t,t)\approx {\nabla }_{{\mathbf{x}}_t}\log q({\mathbf{x}}_t)={\mathbb{E}}_{q({\mathbf{x}}_0)}[{\nabla }_{{\mathbf{x}}_t}\log q({\mathbf{x}}_t|{\mathbf{x}}_0)]={\mathbb{E}}_{q({\mathbf{x}}_0)}[-\frac{{ϵ}_{\theta }({\mathbf{x}}_t,t)}{\sqrt{1-{\bar{\alpha }}_t}}]=-\frac{{ϵ}_{\theta }({\mathbf{x}}_t,t)}{\sqrt{1-{\bar{\alpha }}_t}}$$

所以如果通过 score based 角度来理解 diffusion 的话，

• 在训练过程中，模型学习了 ${ϵ}_{\theta }(x_t,t)$，实际上也就是隐式学习了各个阶段的score function
• 即diffusion通过训练一个 score network来拟合不同t的 ${\nabla }_{{\mathbf{x}}_t}\log q({\mathbf{x}}_t)$，然后依据 Langevin dynamics 逐步逼近真实分布 $q(x)$

优化

对 ${\beta }_t$

DDPM中的 ${\beta }_t$ 是线性变化的，从 $10^{-4}$ 到 $0.02$
后续的论文提出了对此的修改，将linear 改成 cosine-based variance schedule
具体公式如下

$${\beta }_t=\mathrm{clip}(1-\frac{{\bar{\alpha }}_t}{{\bar{\alpha }}_{t-1}},0.999){\bar{\alpha }}_t=\frac{f(t)}{f(0)}\mathrm{where}f(t)=\cos (\frac{t/T+s}{1+s}\cdot \frac{\pi }{2}{)}^2$$

s 是防止t = 0时过小的offset

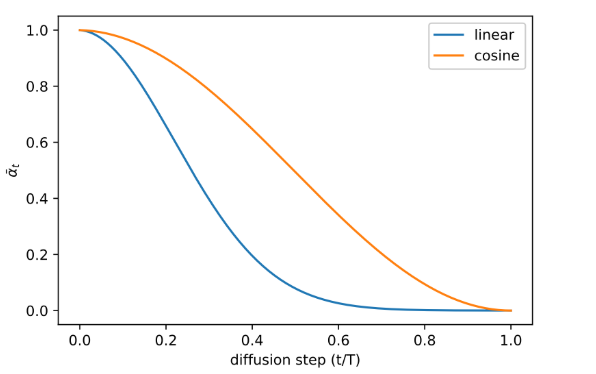
具体的schedule函数的选择是任意的，只要满足两端缓慢变化和中间接近线性就可以

对 ${\Sigma }_{\theta }$

DDPM中固定方差为 ${\beta }_t$ 和 ${\tilde{\beta }}_t$
同改进论文中，提出学习方差

方差定义为

$${\mathbf{\Sigma }}_{\theta }({\mathbf{x}}_t,t)=\exp (\mathbf{v}\log {\beta }_t+(1-\mathbf{v})\log {\tilde{\beta }}_t)$$

现在的损失中是方差无关的，所以需要加入一个能够指导方差学习的项，论文使用

$$L_{\mathrm{hybrid}}=L_{\mathrm{simple}}+\lambda L_{\mathrm{VLB}}$$

其中 $L_{VLB}$ 只与方差有关，关于均值的部分不计算梯度。$\lambda =0.001$

然后说，论文发现这样很难算，最后使用一个time-averaging smoothed version

具体见论文[2102.09672] Improved Denoising Diffusion Probabilistic Models

Conditioned Generation

生成模型通常需要有conditioning information，充当图片的描述或标签

Classifier Guided Diffusion

为了将类别标签加入到diffusion process中
这篇论文 训练了一个 classifier $f\varphi (y|x_t,t)$
生成过程加入了 ${\nabla }_{\mathbf{x}}\log f_{\varphi }(y|{\mathbf{x}}_t)$ 作为指导
有score function

$$\begin{array}{rl}{\nabla }_{{\mathbf{x}}_t}\log q({\mathbf{x}}_t,y)& ={\nabla }_{{\mathbf{x}}_t}\log q({\mathbf{x}}_t)+{\nabla }_{{\mathbf{x}}_t}\log q(y|{\mathbf{x}}_t)\\ & \approx -\frac{1}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)+{\nabla }_{{\mathbf{x}}_t}\log f_{\varphi }(y|{\mathbf{x}}_t)\\ & =-\frac{1}{\sqrt{1-{\bar{\alpha }}_t}}\left({\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)-\sqrt{1-{\bar{\alpha }}_t}{\nabla }_{{\mathbf{x}}_t}\log f_{\varphi }(y|{\mathbf{x}}_t)\right)\end{array}$$

此时 predictor 需要预测的形式就变成

$${\overline{\mathbf{ϵ}}}_{\theta }({\mathbf{x}}_t,t)={\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)-\sqrt{1-{\bar{\alpha }}_t}{\nabla }_{{\mathbf{x}}_t}\log f_{\varphi }(y|{\mathbf{x}}_t)$$

为了控制classifier的影响强弱，可以加入一个weight $w$

$${\overline{\mathbf{ϵ}}}_{\theta }({\mathbf{x}}_t,t)={\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)-\sqrt{1-{\bar{\alpha }}_t}w{\nabla }_{{\mathbf{x}}_t}\log f_{\varphi }(y|{\mathbf{x}}_t)$$

得到 ablated diffusion model(ADM) 和有指导的 ADM-G

DDPM sample 过程

DDIM 过程

Classifier Free Guidance(CFDM)

实际上，通过数学推导可以发现，并不需要一个显式的classifier来得到conditional diffusion
classifier的分布梯度可以重新参数化为

$$\begin{array}{rl}{\nabla }_{{\mathbf{x}}_t}\log p(y|{\mathbf{x}}_t)& ={\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t|y)-{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t)\\ & =-\frac{1}{\sqrt{1-{\bar{\alpha }}_t}}({ϵ}_{\theta }({\mathbf{x}}_t,t,y)-{ϵ}_{\theta }({\mathbf{x}}_t,t))\end{array}$$

记此时模型需要学习的均值为 $\overline{ϵ}(x_t,t,y)$

$$\begin{array}{rl}{\overline{ϵ}}_{\theta }({\mathbf{x}}_t,t,y)& ={ϵ}_{\theta }({\mathbf{x}}_t,t,y)-\sqrt{1-{\bar{\alpha }}_t}w{\nabla }_{{\mathbf{x}}_t}\log p(y|{\mathbf{x}}_t)\\ & ={ϵ}_{\theta }({\mathbf{x}}_t,t,y)+w({ϵ}_{\theta }({\mathbf{x}}_t,t,y)-{ϵ}_{\theta }({\mathbf{x}}_t,t))\\ & =(w+1){ϵ}_{\theta }({\mathbf{x}}_t,t,y)-w{ϵ}_{\theta }({\mathbf{x}}_t,t)\end{array}$$

通过调节参数 $w$ ，可以控制有条件和无条件生成图片影响的比例

真实的训练过程通过随机地消除条件 $y$ 来使模型能够生成无条件图像

Note

为什么要训练无条件下的图像(直观解释)

公式 ${\overline{ϵ}}_{\theta }({\mathbf{z}}_{\lambda },\mathbf{c})=(1+w){ϵ}_{\theta }({\mathbf{z}}_{\lambda },\mathbf{c})-w{ϵ}_{\theta }({\mathbf{z}}_{\lambda })$ 可以重写为 ${ϵ}_{\mathrm{guided}}={ϵ}_{\mathrm{cond}}+(s-1)({ϵ}_{\mathrm{cond}}-{ϵ}_{\mathrm{uncond}})$ (换元整理)
如果从这个角度来看，混合两种图像相当于在原本无条件图像上加上有条件图像的影响。这样的话，无条件下的图像相当于基线，模型生成时在此基础上加上条件的影响。这样的做法可能缘于模型对条件并不敏感，s 可以调控这一点

在GLIDE 论文中，比较了两种策略(CLIP guidance 和 Classifier-free)，发现CFDM的表现更好一些。论文认为在CLIP策略中，模型可能hack CLIP，欺骗CLIP来获得高分，导致表现偏弱

Speed up Diffusion

原始Diffusion的生成相当缓慢，reverse process的 T 可能是几千步。

For example, it takes around 20 hours to sample 50k images of size 32 × 32 from a DDPM, but less than a minute to do so from a GAN on an Nvidia 2080 Ti GPU.

一种可行的方法是进行跳步。限制采样步数 S ，每 $[T/S]$ 步进行采样。此时采样的步数为 $t_1,t_2,..t_s$， $S<T$。
例如$T=1000$，我们指定 $S=100$，每十步进行一次更新，得到更新步数为 $10,20,..1000$。模型直接预测对应步数的噪声进行更新。
这样的做法通过牺牲质量换取了时间。

DDIM

fewer sampling steps

我们可以重写 $q(x_{t-1}|x_t,x_0)$

$$\begin{array}{rl}{\mathbf{x}}_{t-1}& =\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_{t-1}}{\mathbf{ϵ}}_{t-1}\\ & =\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_{t-1}-{\sigma }_t^2}{\mathbf{ϵ}}_t+{\sigma }_t\mathbf{ϵ}\\ & =\sqrt{{\bar{\alpha }}_{t-1}}\left(\frac{{\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{\mathbf{ϵ}}_{\theta }^{(t)}({\mathbf{x}}_t)}{\sqrt{{\bar{\alpha }}_t}}\right)+\sqrt{1-{\bar{\alpha }}_{t-1}-{\sigma }_t^2}{\mathbf{ϵ}}_{\theta }^{(t)}({\mathbf{x}}_t)+{\sigma }_t\mathbf{ϵ}\end{array}$$

引入超参数 $\sigma$ ，第二项前后的分布没有发生变化，则前后 $x_{t-1}$ 是等价的
把整个式子看成是对 $ϵ$ 的变化，则可以得到 $x_{t-1}$ 的分布

$$q_{\sigma }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)=\mathcal{N}\left({\mathbf{x}}_{t-1};\sqrt{{\bar{\alpha }}_{t-1}}\left(\frac{{\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{\mathbf{ϵ}}_{\theta }^{(t)}({\mathbf{x}}_t)}{\sqrt{{\bar{\alpha }}_t}}\right)+\sqrt{1-{\bar{\alpha }}_{t-1}}{\sigma }_t^2{\mathbf{ϵ}}_{\theta }^{(t)}({\mathbf{x}}_t),{\sigma }_t^2\mathbf{I}\right)$$

从式子上看，$\sigma$ 是无所谓大小的，在DDPM的分布中

$${\tilde{\beta }}_t={\sigma }_t^2=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t$$

我们引入一个 $\eta$ ，设 ${\sigma }^2=\eta \tilde{\beta }$，则当 $\eta =1$ 时，为DDPM，是一个马尔可夫链过程，此时每一个 $t-1$ 状态依赖于上一个时间步的采样。
而如果 $\eta =0$，分布的随机性消失，我们得到一个非马尔可夫链过程(一个确定性函数)。这个过程是确定性的(没有方差)，即给定一个初始的高斯噪声，依据公式最终得到的图像是一致的，这样的方法为DDIM
由于这样的确定性/非马尔可夫，我们没有必要一步步采样，可以通过跳步来加速图像生成。

实际效果参考如下(FID score)

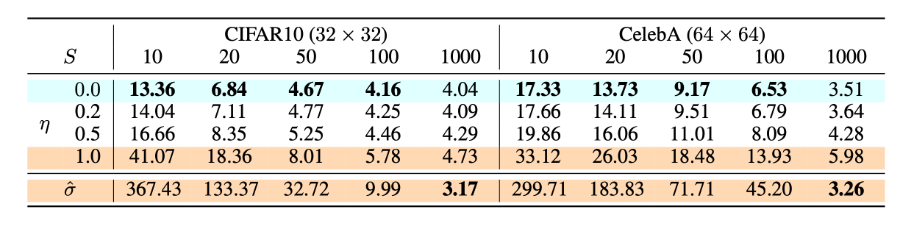
在实际上生成中，每一次生成经过两个步骤

• 依据当前的 $x_t$ 估计 $x_0$
• 根据公式更新 $x_t$

Note

为什么DDIM需要多次采样

既然反向去噪过程是一个确定性的函数，为什么需要多次采样
直觉上理解大概是

• 尽管反向是确定的，但是 $x_0$ 不是已知的，通过估计来进行采样，如果一步跨度过大，误差也会增大
• 尽管给定 时间步表和初始噪声，模型生成结果会是确定的，但是并不见得这个结果是最优的，通过调整时间步可能得到更好的结果

相比于 DDPM，DDIM 有以下优势

• 能用更少的步骤生成高质量图片
• 拥有一致性，由于DDIM的确定性，样本 conditioned on the same latent variable 会有相近的高层特征(高层语义上相近)
  • 相同的噪声输入会有相近的结果
• 一致性使得，DDIM在latent variable中的插值会对应语义上平滑过渡的生成结果
  • 如进行线性插值 $x_T^{\prime \prime }=\alpha x_T=(1-\alpha )x_T^{\prime }$ ，生成图像会在语义上连续变化

DDIM实际上不完全是一种模型，DDIM重新参数化了反向过程(转化为非马尔可夫过程)，可以被理解为广义的扩散模型框架。DDIM的采样方法适用了DDPM方法训练的模型，用于加速采样。

DDPM，NCSN可以被统一在 SDE(随机微分方程)框架中，而DDIM实际上将SDE转化为了ODE(常微分方程)，这个ODE的求解本身是要求多步的。
更详细的参见 👈 待补

• 如何理解扩散模型中的SDE？
• 生成扩散模型漫谈（五）：一般框架之SDE篇 - 科学空间|Scientific Spaces
• [2011.13456] Score-Based Generative Modeling through Stochastic Differential Equations

SDE 框架

DDPM 和 NCSN 都是离散角度的描述，如果使用SDE(Stochastic Differenctial Equations)连续化地统一描述的话
扩散模型的前向过程为

$$d\mathbf{x}={\mathbf{f}}_t(\mathbf{x})dt+g_{t}d\mathbf{w}$$

前面$f(x)$是偏移项，后面 $g_t$ 是扩散系数，$dw$ 是标准布朗运动
将式子理解为离散情况下的极限，即 $dx={\lim }_{\Delta t\to 0}\left(x_{t+\Delta t}-x_t\right)$ 可以进一步得到

$${\mathbf{x}}_{t+\Delta t}={\mathbf{x}}_t+\underset{\mathrm{确定部分}}{\underbrace{{\mathbf{f}}_t({\mathbf{x}}_t)\Delta t}}+\underset{\mathrm{随机部分}}{\underbrace{g_t\sqrt{\Delta t}\epsilon }},\epsilon \sim \mathcal{N}(0,\mathbf{I})$$

这个前向SDE对应一个逆向SDE，可以由概率的引入推导出， 形式为

$$d\mathbf{x}=\left[f_t(\mathbf{x})-g_t^2{\nabla }_{\mathbf{x}}\log p_t(\mathbf{x})\right]dt+g_{t}d\mathbf{w}$$

这一形式接近于朗之万采样，也接近于DDIM中的Diffusion扩展(这个要早于DDIM)。
基于此，我们可以将 DDPM 和 NCSN 都纳入这个框架，区别只在于 $f,g$ 的不同，其中DDPM为VP SDE (Variance Preserving)，NCSN为VE SDE(Variance Exploding)，方差紧缩和爆炸源于主导的元素不同。
我们将式子中的梯度称为 score function，目标是训练模型逼近这个function。

还有一种角度是，去掉随机部分，得到一个确定性的逆向过程，称 概率流常微分方程(PF-ODE)
采样时可以使用任意 ODE Solver 求解，通常在 $t=ϵ$ 时停止，将$x_{ϵ}$ 作为近似值接受

Progressive Distillation

通过蒸馏训练好的 deterministic sampler(DDIM)，训练 student DDIM，使得 studet DDIM的每一步都等效于 teacher DDIM 的两步

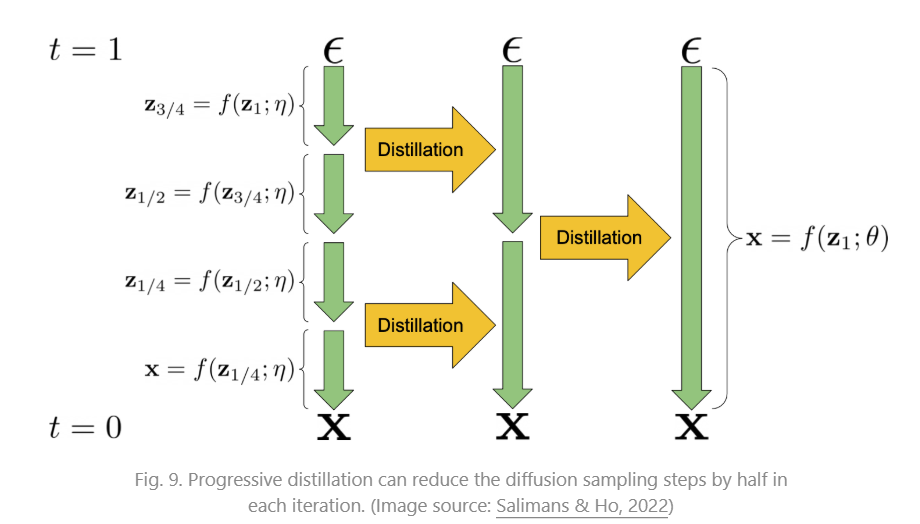
具体算法为

Consistency Models

尝试学习一个 给定noisy data point $x_t,t>0$，直接映射到原图 $x_0$ 的模型，称为 consistency model
在同一个diffusion sampling trajectory的过程都映射回同一张图(origin)，称为 self-consistency property

形式化描述的话，给定一个trajectory，$\left\{x_t|t\in [ϵ,T]\right\}$ ，consistency function $f$ 定义为 $f:(x_t,t)\to x_{ϵ}$ (接受任意时刻的noisy data point，映射到原图)。任意时刻的函数值都相等 $f(x,t)=f(x_t^{\prime },t^{\prime })=x_{ϵ}$ ，特别的，当 $t=ϵ$ 时，$f$ 是一个identify function
模型学习这个函数，可以被描述为

$$f_{\theta }(\mathbf{x},t)=c_{\mathrm{skip}}(t)\mathbf{x}+c_{\mathrm{out}}(t)F_{\theta }(\mathbf{x},t)$$

其中 $c_{\mathrm{skip}}$ 和 $c_{\mathrm{out}}$ 在 $t=ϵ$ 时分别为 1，0，使得式子可微且满足上述条件

模型可以一次性生成原图，但是多步生成质量更高

这和DDPM的区别是什么？

DDPM 并不存在一致性的约束
DDPM在训练之后能得知的只有当前图像上的纯噪声是什么，而无法得知真实世界中当前图像和原图的关系。DDPM每一步都在马尔可夫链过程下进行，逆向的下一步取决于上一步的结果(我们只建模了这个过程)。
所以DDPM只能一步步生成。

DDIM改变了这一建模($\eta =0$)，逆向过程变成一个确定性函数，是离散化 概率流常微分方程。但是本质仍然是 逆向生成过程，生成过程依赖于 score function，score function的估计仍然是local 的(没有一致性约束)，所以逐步生成效果更佳

而CM通过引入一致性约束缓解了这一点，理论可以一步生成

训练

论文提供了两种训练方法，分别是蒸馏和从头训练

Consistency Distillation (CD)

蒸馏方法

我们已经确定了ODE，只要每次采样，使预测的结果与 ODE的解 距离减小就好，但是这样的训练每次都需要求解一遍 ODE，效率很低。
另一种方法是使一条轨迹上相邻两个点的模型输出一致
训练的损失为

$$\begin{array}{rl}{\mathcal{L}}_{\mathrm{CD}}^N(\theta ,{\theta }^{-};\varphi )& =\mathbb{E}[\lambda (t_n)d(f_{\theta }({\mathbf{x}}_{t_{n+1}},t_{n+1}),f_{{\theta }^{-}}({\hat{\mathbf{x}}}_{t_n}^{\varphi },t_n)]\\ {\hat{\mathbf{x}}}_{t_n}^{\varphi }& ={\mathbf{x}}_{t_{n+1}}-(t_n-t_{n+1})\Phi ({\mathbf{x}}_{t_{n+1}},t_{n+1};\varphi )\end{array}$$

其中

• $\varphi ()$ 是ODE solver
• ${\hat{x}}_{t_n}^{\varphi }$ 是从 $x_{t_{n+1}}$ 估计 $x_{t_n}$
• n 服从选定时间步的均匀分布
• ${\theta }^{-}$ 是 $\theta$ 的EMA版本，用于稳定训练
• $d()$ 是距离公式，需要满足 $\ge 0$ 且当 $x=y$，$d(x,y)=0$
• $\lambda ()$ 是权重，论文中设定为 1

Note

什么是EMA

EMA(Exponential Moving Average) 指数移动平均

$${\theta }_{EMA}^{(t)}=\alpha \cdot {\theta }_{EMA}^{(}t-1)+(1-\alpha )\cdot {\theta }^{(t)}$$

其中$\alpha$ 通常设置为接近1，提供一个变化平稳的参数，可用于提高泛化性能，平稳模型训练等

Consistency Training(CT)

CD中，我们使用了预训练模型来充当score function，重新训练需要另外一种方式来估计它。论文证明了一种新的估计方法

$$\nabla \log p_t({\mathbf{x}}_t)=-\mathbb{E}\left[\frac{{\mathbf{x}}_t-\mathbf{x}}{t^2}|{\mathbf{x}}_t\right]$$

于是得到损失为

$$\begin{array}{l}{\mathcal{L}}_{\mathrm{CT}}^N(\theta ,{\theta }^{-})\\ ={\mathbb{E}}_{\mathrm{n}-\mathrm{M}[1,N-1],\mathbf{x}\sim p_{\mathrm{dys}},\mathbf{z}\sim \mathcal{N}(0,1)}\left[\lambda (t_n)d\left({\mathbf{f}}_{\theta }(\mathbf{x}+t_{n+1}\mathbf{z},t_{n+1}),{\mathbf{f}}_{{\theta }^{-}}(\mathbf{x}+t_n\mathbf{z},t_n)\right)\right]\end{array}$$

• 其中 $z\in N(0,1)$

然后是一些实验结果

• Diffusion > CD > diffusion distillation > CT
• Heum ODE 效果好于 Euler’s first-order solver，更高阶更精准
• LPIPS 作为距离好于 L1 L2
• 更小的N(步数)收敛更快但效果更差

Latent Variable Space

Latent diffusion model(LDM) 在 latent space 中进行图像处理(加噪去噪)
LDM 发现图像的大多数bits都起感知细节上的作用，图像的语义和概念性的部分在经过大程度的压缩后仍然能够保留。所以LDM不在pixel space 上进行图像去噪而是在latent space中，降低了运算量

LDM的做法有两个阶段

• perceptual compression process
• diffusion process

在perceptual compression process阶段，LDM使用一个autoencoder $\mathcal{E}$ 压缩输入图像 $x\in {\mathbb{R}}^{H\times W\times 3}$ 到更小的 $\mathbf{z}=\mathcal{E}(\mathbf{x})\in {\mathbb{R}}^{h\times w\times c}$ 。downsampling rate为 $f=H/h=W/w=2^m$ ，在图像生成最后，通过一个 decoder $\mathcal{D}$ 重新构造图像 $\tilde{x}=\mathcal{D}(z)$
论文提出两种用于autoencoder 训练的正则化方法，避免latent spaces 的高方差问题

• KL-reg：一个 KL 的penalty，与VAE相近
• VQ-reg：在decoder层加一个vector quantization layer，类似 VQVAE

diffusion process作用于latent vector $z$。这部分的架构是一个time-conditioned U-Net，加上一个cross-attention来获取conditioning information(class, semantic maps…)。每一种类型的conditioning information都有一个对应的 demain-specific encoder ${\tau }_{\theta }$ 对应进行编码

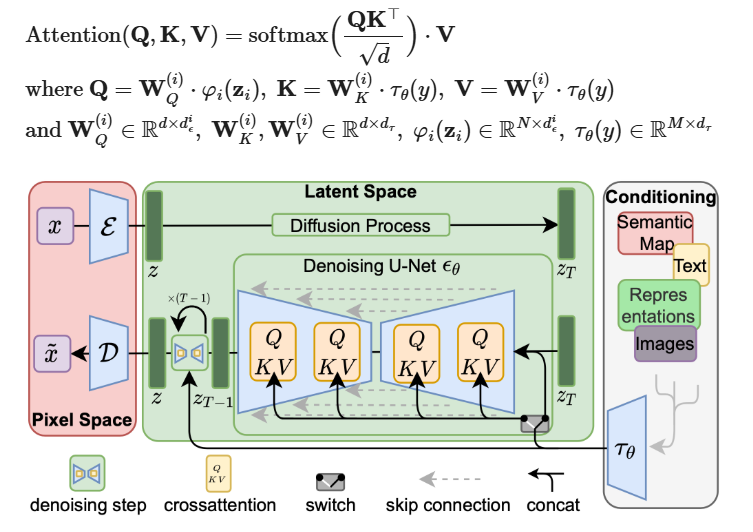
Scale up Generation Resolution and Quality

为了生成高像素的图像，一种方法是使用多个diffusion 构建pipeline

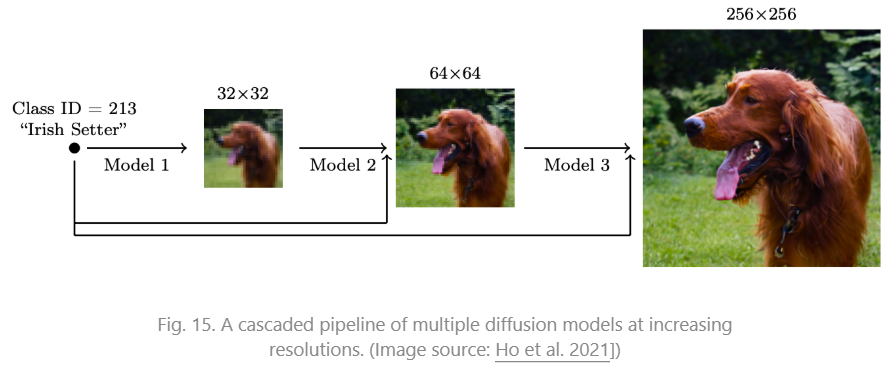
在训练过程中加入 noise conditioning augmentation对最终图像的质量至关重要。设输入图像为 $z$，输出图像为 $x$ ，我们需要对 $z$ 进行strong data augmentation再作为下一个diffusion的输入，即$p(x|z)$

conditioning noise 减少了compounding error
在推理时不需要 conditioning noise

论文发现，最有效的方法是对低像素图像使用 Gaussian noise，对高像素图像使用 Gaussian blur，论文探索了两种数据增强的方法

• Truncated conditioning augmentation: 在低分辨率图像还没完全生成时提前中止
• Non-truncated conditioning augmentation: 完全运行低分辨率的生成，然后添加噪声

另一种方法是 unCLIP
unCLIP高度依赖于CLIP text encoder进行text-guided images生成，给定预训练CLIP和相同数据集训练的diffusion model，我们可以计算 CLIP text embedding $c^t(y)$ 和 image embedding $c^i(x)$
unCLIP同时学习两个模型

• prior model $P(c^i|y)$：给定text $y$ 输出 CLIP image embedding $c^i$
• decoder $P(x|c^i,[y])$：给定CLIP image embedding 和 y(可选) 生成图像 $x$

两个模型生成图像的过程可以写成

$$\underset{{\mathrm{c}}^{\mathrm{i}}\mathrm{is}\mathrm{deterministic}\mathrm{given}\mathrm{x}}{\underbrace{P(\mathbf{x}|y)=P(\mathbf{x},{\mathbf{c}}^i|y)}}=P(\mathbf{x}|{\mathbf{c}}^i,y)P({\mathbf{c}}^i|y)$$

这样就与 conditional generation 等价

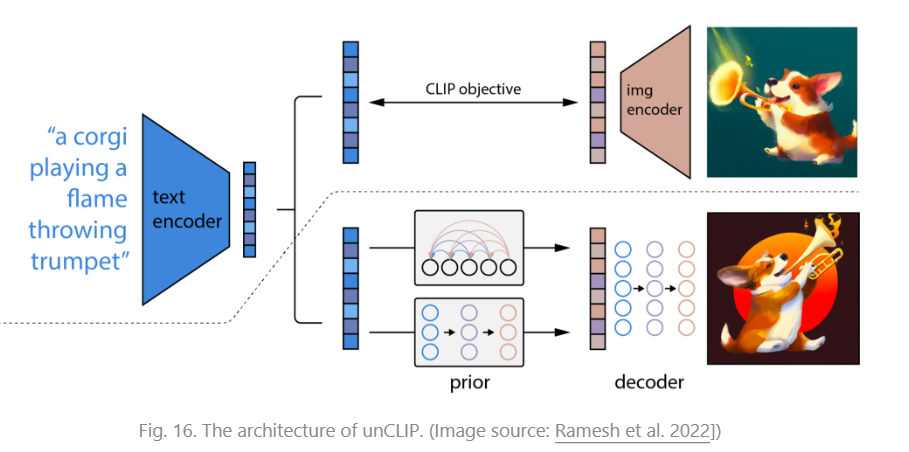
给定一个文本 $y$，CLIP 先生成 text embedding $c^t(y)$，一个diffusion/autoregresssive prior $P(c^i|y)$ 处理这个 CLIP text embedding 得到 image embedding，然后通过一个 diffusion decoder $P(x|c^i,[y])$ 生成图像。
这样做有几个好处

• 由于CLIP事先学习了图像和文本的对应关系，所以使用CLIP 的latent space，修改输入文本能够实现 zero-shot image manipulation
• 生成图像时能使用图像作为输入(CLIP进行图像编码)来生成图像的变体，同时保证图像的语义

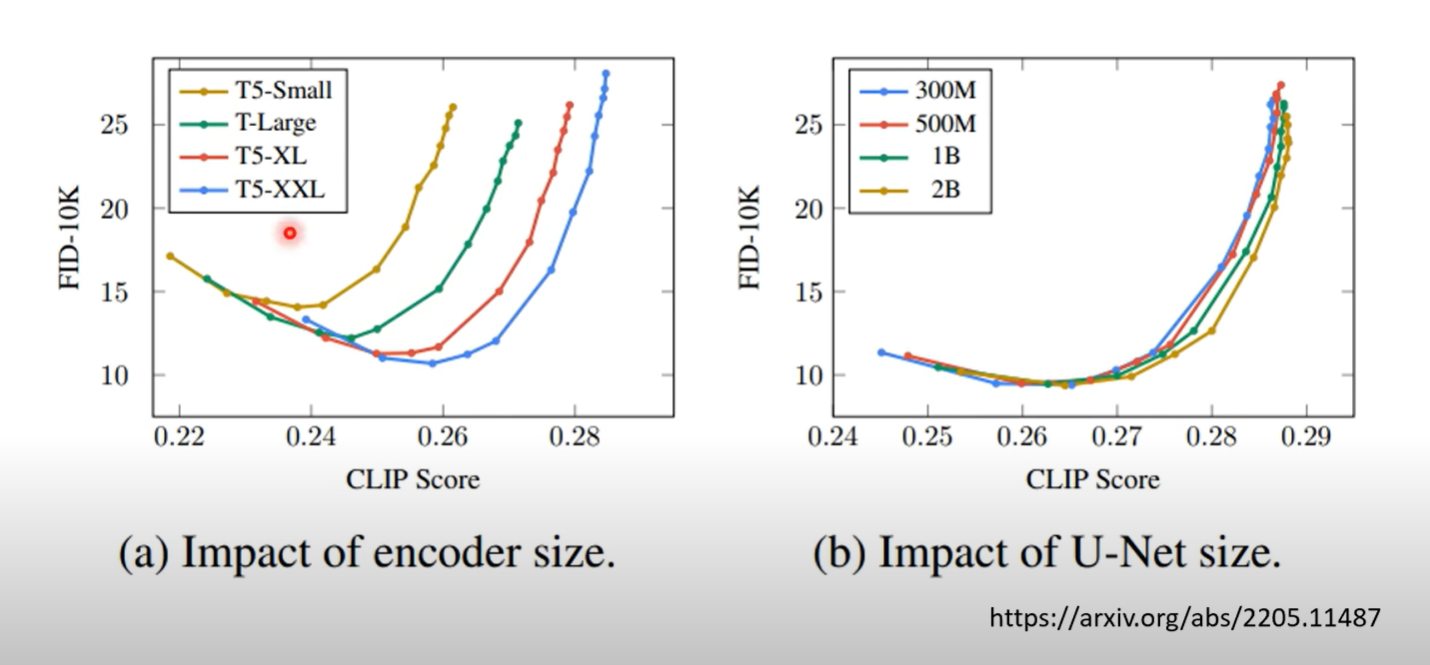
相比于CLIP，Imagen 使用预训练语言模型(frozen-T5-XXL text encoder)来编码文本输入。谷歌的实验指出，更大的语言模型能够有更好的图像生成效果和图像与文本的对齐能力

论文发现，当使用classifier-free guidance的时候，增大 $w$ 会导致生成结果更满足文本但是图片效果更差(worse image fidelity)。论文指出这是因为 train-test mismatch。训练时数据 $x$ 在 $(-1,1)$ 之间，但是($w$增大时)测试时生成的图像并非如此。所以论文提出两种thresholding策略

• Static thresholding：clip x 到 $(-1,1)$ 之间
• Dynamic thresholding：选取一个百分位数的pixel value $s$，如果这个数大于$1$，进行裁剪$(-s,s)$并除以 $s$

然后就是谷歌常用大规模实验和调参

Model Architecture

有两种diffusion常用的模型架构: U-Net and Transformer

U-Net

[1505.04597] U-Net: Convolutional Networks for Biomedical Image Segmentation
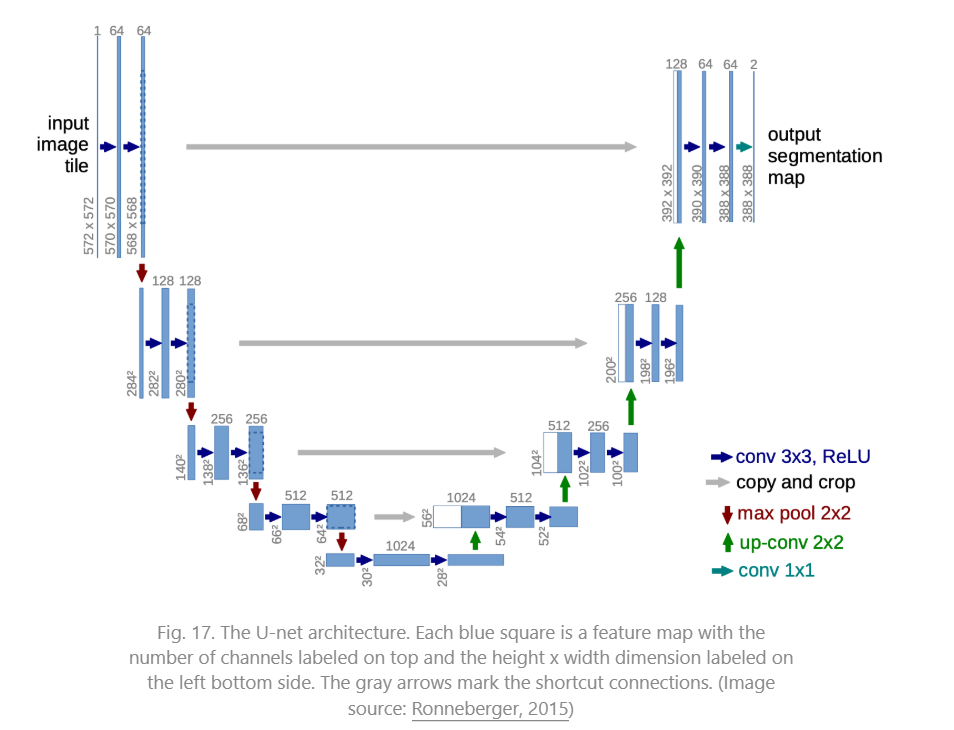
Downsampling stack and an upsampling stack

• Downsampling: 每一步 $3\times 3$ convolutions(unpadded)，加一个 ReLU 和 $2\times 2$ 的max pooling(stride 2)。每一步channels数量翻倍
• Upsampling: up convolution $2\times 2$，加上内部 $3\times 3$ 的ReLU。每一步channels数量减半
• shortcuts: 对应层(down 和 up)间有跳连，为 upsampling process提供high-resolution features

另外的，作为U-net的一个补充
为了能够为图像生成加上额外的条件，ControlNet 复制了U-net作为旁路处理额外条件 $c$

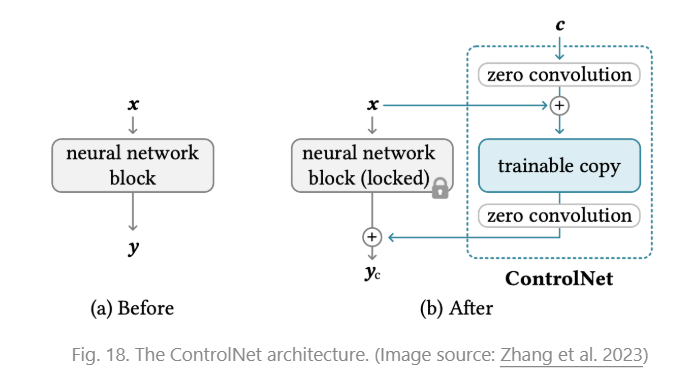
ControlNet 做法如下

1. 冻结原参数 $\theta$
2. 克隆原参数 ${\theta }_c$ 到旁路
3. 在克隆参数上下加上 zeor convolution($1\times 1$，0初始化)
4. 输出更改为 $y_c=F_{\theta }(x)+Z_{{\theta }_{z2}}(F_{{\theta }_c}(x+Z_{{\theta }_{z1}}(c))$

这个模型极其像LoRA(指看上去像)
为什么要加入两个0初始化的卷积层，可能的解释是 这样训练从0开始，一开始模型的行为不会有太大变化，也不会太受condition c影响。这样的话有利于模型平稳训练和过渡

Diffusion Transformer

DiT

DiT是以ViT(Vision Transformer)为基础的模型，谈DiT之前得先谈谈ViT

首先，CNN具有归纳偏置(Inductive Bias)，在使用CNN的时候，存在以下假设

• 局部性：图像有意义的模式由局部相邻像素组成(通常如此)
• 平移不变性：特征与位置无关(通常如此)
• 层次结构，空间不变性(pooling)，通道独立性 在这些假设下，有的在多数场景下适用，使得CNN“天然具有先验知识”，在少量样本中容易学习
  而Transformer并没有这样的能力，需要大量数据来学习局部性等信息，虽然适用范围大，但是少量数据表现可能不如CNN类模型

ViT与上述基本一致，有一系列Transformer+vision的优缺点，其简单实用，成为Transformer用于视觉的代表作

ViT将图片分为多个patch($16\times 16$)，再将patch投影为固定长度的向量送入Transformer，用与Transformer一样的encoder进行操作。在对图像分类任务中，输入序列尾部会有一个特殊token，对应的输出为最后的类别预测

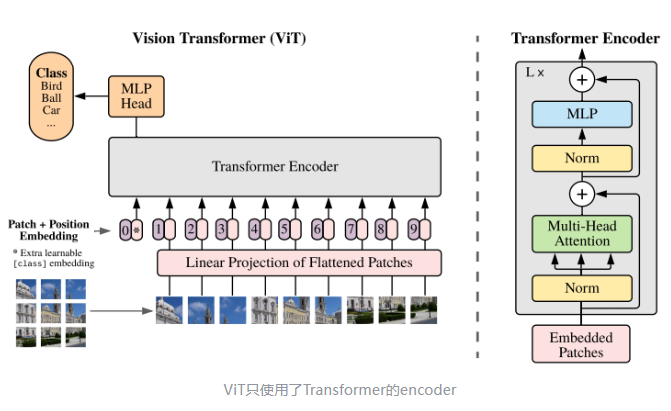
主要的操作在于 patch embedding
设定patch大小 $p$，将输入 $I\times I\times C$ 拆分为 $\frac{I\times I}{p\times p}$ 个patch，一个patch是一个输入token。然后加上特殊token cls 加入到 transformer 的encoder中(positional embedding, attention, layer norm, MLP)。

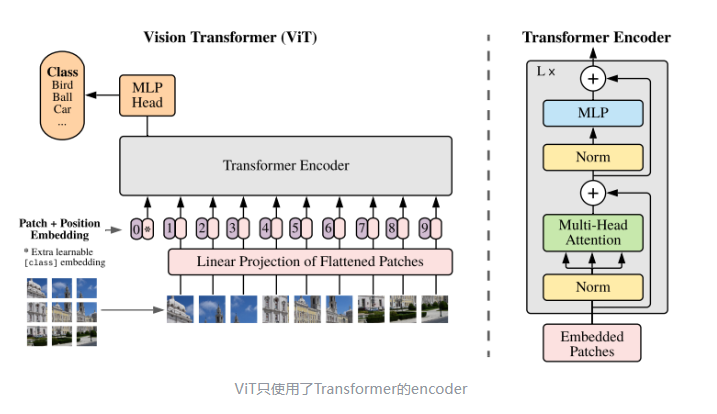
可以不加入特殊token，使用所有token输出的token取平均(average pooling)

一些论文的实验结果

• 位置编码不是很重要，认为是 patch 的位置对模型来说并不难辨认
• 在小规模数据集上，使用CNN based模型效果更好

DiT 不同的是，它是LDM based 的ViT，处理图像的空间是 latent space

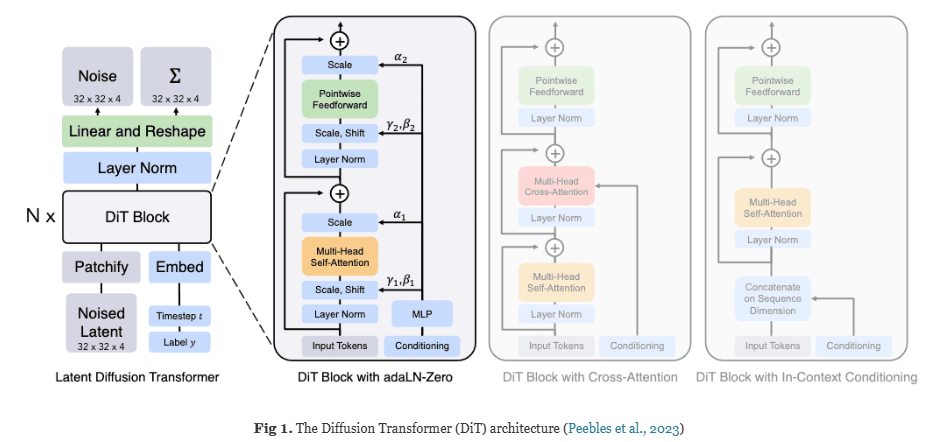
DiT将图像的latent representation和condition，timestep的embedding作为输入，探讨了三种形式

• In-Context conditioning
  • 将condition和timestep直接作为图像token的一部分进行处理，带来的GFLOPs变化很少
• Cross Attention
  • 将 $t$ 和 $c$ 的 Embedding 连接成一个长度为2的 Sequence，带来的GFLOPs的开销约为15%
• Adaptive Layer Norm(adaLN)
  • ${\mathbf{x}}^{\prime }=\gamma \cdot \frac{\mathbf{x}-\mu (\mathbf{x})}{\sigma (\mathbf{x})}+\beta \mathrm{where}\mathbf{x},{\mathbf{x}}^{\prime }\in {\mathbb{R}}^d$
  • 其中 $\gamma$，$\beta$ 是通过 $t,c$ 回归得到的

MLP除了回归 $\gamma ,\beta$ 之外，还回归 $\alpha$(残差连接的缩放系数)。通过初始化 MLP 使得三个变量初始值都为0，有利于稳定训练
模型输出noise prediction 和 对角协方差

Summary

• Diffusion 是一个理论较为坚实的idea，是相当有意思的想法。Diffusion 兼顾了模型的tractability 和 flexibility，既能够 analytically evaluated 和 cheaply fit data，训练和sample也不会太难。在生成模型领域一定有相当的地位
• Diffusion的推理时间仍然过长(长于GAN)，这有待解决

在现在看来，diffusion的势头略有些衰落，尽管有基于diffusion的新工作出现(例如基于扩散模型的语言模型)，但是没取得足够瞩目的成功
在GPT-4o的生图能力(大概是自回归)出现后，diffusion 在生图上是否能够与之对抗还有待更多的工作出现。

even if you don’t believe diffusion models are the future, I don’t think you can completely ignore them either and they will probably have at the very least interesting niche applications

References

Basically notes from Weng Lilian’s blog

• 由浅入深了解Diffusion Model
• What are Diffusion Models? | Lil’Log 👈
• Introduction to Diffusion Models for Machine Learning 👈
• Fetching Title#ex7y
• Generative Modeling by Estimating Gradients of the Data Distribution | Yang Song 👈
• 扩散模型解读 (一)：DiT 详细解读
• ViT（Vision Transformer）解析
• 从DDPM到Consistency Models（笔记）
• 一步生成的扩散模型：Consistency Models
• 生成扩散模型漫谈（五）：一般框架之SDE篇 - 科学空间|Scientific Spaces
• 如何理解扩散模型中的SDE？
• plus 众多已在文中加入链接的原论文