Linear Attention (working on GatedDeltaNet)

主要是对文章的理解和笔记

简史

FROM 线性注意力简史：从模仿、创新到反哺 - 科学空间|Scientific Spaces

简史中需要补充RWKV部分

Softmax Attention

Annotation

$$\begin{array}{c}{\mathbf{q}}_i,{\mathbf{k}}_i,{\mathbf{v}}_i,{\mathbf{o}}_i\in {\mathbb{R}}^{d\times 1}\\ \mathbf{Q}=[{\mathbf{q}}_1,{\mathbf{q}}_2,\dots ,{\mathbf{q}}_n{]}^{\top }\in {\mathbb{R}}^{n\times d}\\ \mathbf{K}=[{\mathbf{k}}_1,{\mathbf{k}}_2,\dots ,{\mathbf{k}}_n{]}^{\top }\in {\mathbb{R}}^{n\times d}\\ \mathbf{V}=[{\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_n{]}^{\top }\in {\mathbb{R}}^{n\times d}\\ \mathbf{O}=[{\mathbf{o}}_1,{\mathbf{o}}_2,\dots ,{\mathbf{o}}_n{]}^{\top }\in {\mathbb{R}}^{n\times d}\end{array}$$

Softmax Attention通常指 Attention is all you need 中的Attention机制

$$\mathbf{O}=\mathrm{softmax}(\mathbf{Q}{\mathbf{K}}^{\top }+\log \mathbf{M})\mathbf{V}$$

QK为一组，负责生成Attention Score，VO是一组，通过对V的加权得到O，所以QK和VO的维度 $d$ 可以不同

注意区分 GQA 等KV成组的情况，这里的一组指的是运算顺序，而共享KV是注意力头的角度

这里的M是掩码矩阵，一般是0或1，0为掩码，经过element-wise的log，$log0$置为$-inf$，在softmax中分配得到的权重就是0

另外的，此处应该有一个缩放因子，可以被吸收到QK中所以省略

Softmax Attention最终的形式为

$${\mathbf{o}}_t=\frac{{\sum }_{j=1}^t\exp ({\mathbf{q}}_t^{\top }{\mathbf{k}}_j){\mathbf{v}}_j}{{\sum }_{j=1}^t\exp ({\mathbf{q}}_t^{\top }{\mathbf{k}}_j)}$$

分子是加权和，分母是softmax归一化因子，分母主要是保持数值稳定性，如果对最终输出O进行RMSNorm，分母会被消去，所以认为重点是分子部分

这里说的RMSNorm实际上是简化的计算，在单头注意力+不进行projection的情况下是成立的，在MHA中，每个头对应的分母不同，所以不能这么说 但是重点在于 分子是主要决定注意力计算结果的部分，softmax本身/分母本身只是一个归一化的方法

化简得到

$$\mathbf{O}=\exp (\mathbf{Q}{\mathbf{K}}^{\top }+\log \mathbf{M})\mathbf{V}=(\exp (\mathbf{Q}{\mathbf{K}}^{\top })\odot \mathbf{M})\mathbf{V}$$

其中$\odot$是hadmard积(逐元素积)。如果把这里的V改成$n\times 1$的向量，就可以得到分母的计算(softmax按行计算)，这种形式也就方便加回分母。 可以看出，softmax attention的重点在于注意力分数矩阵的计算，空间和时间都是$n^2$，FlashAttention不用存储整个attention score，降低了空间复杂度但是时间复杂度仍然不变

这里实际上，QK相乘是$n^2$，exp是$n^2$，逐元素掩码也是$n^2$，与V相乘也是$n^2$，然后除法(归一化)也是$n^2$

Linear Attention

一开始的Linear Attention是模拟softmax attention
一种最简单的做法是去掉exp

$$\mathbf{O}=(\mathbf{Q}{\mathbf{K}}^{\top }\odot \mathbf{M})\mathbf{V}$$

为什么这样是线性的？
对于非Causal的注意力计算(没有M)，可以通过矩阵交换律改变计算顺序得到线性的计算

$$O=Q(K^{T}V)$$

原本$Q{K}^T$的时间复杂度是 $O(n^{2}d)$，现在$K^{T}V$的时间复杂度是$O(n{d}^2)$，与Q相乘仍然是$O(n{d}^2)$

对于Causal的注意力，可以借鉴非Causal的形式，尝试能不能改变计算顺序/方式
与M的计算(保留$Q{K}^T$)一定会出现$n^2$的矩阵，复杂度无法避免，直接改写成分量的形式

$${\mathbf{o}}_t=\sum _{j=1}^t{\mathbf{v}}_j({\mathbf{k}}_j^{\top }{\mathbf{q}}_t)=\sum _{j=1}^t({\mathbf{v}}_j{\mathbf{k}}_j^{\top }){\mathbf{q}}_t=\left(\sum _{j=1}^t{\mathbf{v}}_j{\mathbf{k}}_j^{\top }\right){\mathbf{q}}_t$$

这里的 $v_j{k}_j^T{q}_t$ 相乘，可以看成是矩阵相乘(主要是因为是v的加权和)，那就可以使用结合律，将同属于$\sum$的vk放一起
将括号部分标记为 $S_t$，就有

$${\mathbf{o}}_t={\mathbf{S}}_t{\mathbf{q}}_t,{\mathbf{S}}_t={\mathbf{S}}_{t-1}+{\mathbf{v}}_t{\mathbf{k}}_t^{\top }$$

这里 $v_j{k}_j^T$，也就是$S_t$得到的是一个$d\times d$的矩阵，相关计算都是常数级的，给定长度为n的序列，时间复杂度就是线性$O(n)$的
这是一个线性RNN，体现在 状态的更新(对$S_t$的变换)和输出的计算都是线性的(而没有非线性函数的引入)

为了模仿softmax attention，一些工作(Performer、RFA)会给原式加上分母进行归一化，为了归一化就需要保证非负，于是引入QK的非负激活函数。但在后来的研究中(The Devil in Linear Transformer)发现在序列长度维度归一化(原本softmax做的)并不能带来(很好的)数值稳定性，不如事后归一化

$$\mathbf{O}=\text{RMSNorm}((\mathbf{Q}{\mathbf{K}}^{\top }\odot \mathbf{M})\mathbf{V})$$

所以关于非负激活函数，苏神认为不是很重要，有工作表明可能不加已经足够好

Forget Gate

$${\mathbf{o}}_t={\mathbf{S}}_t{\mathbf{q}}_t,{\mathbf{S}}_t={\mathbf{S}}_{t-1}+{\mathbf{v}}_t{\mathbf{k}}_t^{\top }$$

既然线性Attention是一个线性RNN，那么RNN的固有问题就一定会出现 “当叠加的token足够多时，每个token的信息占比都会变得极小，于是单靠固定大小的St 矩阵甚至无法准确重建任意一个token，直观类比就是每个token的记忆都变得模糊不清”
所以需要设置遗忘机制

RetNet的做法是

$${\mathbf{o}}_t={\mathbf{S}}_t{\mathbf{q}}_t,{\mathbf{S}}_t=\gamma {\mathbf{S}}_{t-1}+{\mathbf{v}}_t{\mathbf{k}}_t^{\top }$$

$\gamma \in (0,1)$ 是衰减因子，可能是常数，可能是可训练参数等等形式。衰减因子使得模型逐渐遗忘更久远的历史信息，从而保证新token的信息。是一种语言模型的就近原则(Recency Bias)

RetNet还给QK加上了RoPE，这样使得衰减因子变成$\gamma e^{i\theta }$。关于给RNN加入位置编码的做法似乎暂未有广泛的共识

一个简单的推广是将衰减因子替换成与时间$t$相关的函数 ${\gamma }_t$，例如工作SSM
另一个做法(DFW, Mamba)是将它推广到与输入相关(data-dependent decay)，与非线性RNN(GRU，LSTM)类似，只是与状态本身$S_t$无关(避免非线性的引入)

Test-Time Training

Test Time Training是一个思想/做法，旨在将为序列模型引入online learning，在测试时更改参数
TTT提出可以使用优化器来构建RNN。SGD，Adam等优化器本身可以被看成是一个RNN，模型参数是其状态，每接受一个新的batch，会输出梯度并更新状态。利用优化器的recurrent，可以将模型改造成recurrent。
TTT的基本逻辑是 将KV作为上下文对$(k_i,v_i)$，设计损失函数$\mathcal{L}(f(S_{t-1},k_t),v_t)$，更新模型参数后得到最终输出 $o_t=f(S_t,q_t)$
数学形式可以写成

$${\mathbf{o}}_t=\mathbf{f}({\mathbf{S}}_t;{\mathbf{q}}_t),{\mathbf{S}}_t={\mathbf{S}}_{t-1}-{\mathbf{\eta }}_t{\nabla }_{{\mathbf{S}}_{t-1}}\mathcal{L}(\mathbf{f}({\mathbf{S}}_{t-1};{\mathbf{k}}_t),{\mathbf{v}}_t)$$

$f$是模型，$\eta$ 是学习率(可以是data dependant)

这里可以理解为，TTT实际上在测试的时候构建了一个新的RNN，这个模型进行状态更新的目的是为了编码/压缩训练数据，所以损失 $\mathcal{L}$ 定义的是一个与模型原能力本质一致但是数据特化的任务，这个任务希望把测试数据的偏移/新的特性压缩到模型中。
所以TTT并不是全新的Linear Attention，是给出了一种Linear Attention RNN状态更新方法的思路

至于为什么用KV，我的理解是不同方法各不相同，各有设计；使用KV是线性注意力常用的方法。注意力中，同一个输入X进行三种不同转化得到QKV，理想情况下它们遵循同一种逻辑，表达是一致的。如果现在测试数据存在偏移，即QKV无法按我们希望的方式去提取X的信息，可能可以通过模型是否理解KV之间映射得到反馈。 待深入

TTT虽然提到了使用优化器作为更新状态的依据，但是有的时候并不需要显式的经过 损失—梯度—更新的过程，通过定义可以显式求导的损失(如L2损失)可以隐式地构建TTT
所以与其说TTT是额外加入的方法/工具，实际上是一个数学框架/角度

DeltaNet

最早的线性Attention对应的损失函数是 $-v^T(Sk)$

最早的线性Attention并不用于语言建模，所以这个损失比较陌生
这里仍然是希望让通过 $S,k$ 得到$v$，只是将 $f()$ 设置为简单的线性乘法

这样的损失通过内积计算相似性，有一定道理，但它是无下界的，容易导致S趋向无穷
一个更理想更直接的损失可能是MSE/L2 Loss，即 $\frac{1}{2}\Vert \mathbf{S}\mathbf{k}-\mathbf{v}{\Vert }^2$ DeltaNet便使用了这样的损失

$${\mathbf{o}}_t=\mathbf{f}({\mathbf{S}}_t;{\mathbf{q}}_t),{\mathbf{S}}_t={\mathbf{S}}_{t-1}-\underset{{\nabla }_{{\mathbf{S}}_{t-1}}\frac{1}{2}\Vert {\mathbf{S}}_{t-1}{\mathbf{k}}_t-{\mathbf{v}}_t{\Vert }^2}{\underbrace{{\eta }_t({\mathbf{S}}_{t-1}{\mathbf{k}}_t-{\mathbf{v}}_t){\mathbf{k}}_t^{\top }}}$$

${\eta }_t$ 是一个常数，不妨设其为1方便分析
将式子拆开可以得到

$$\begin{array}{rl}{\mathbf{S}}_t& ={\mathbf{S}}_{t-1}-({\mathbf{S}}_{t-1}{\mathbf{k}}_t-{\mathbf{v}}_t){\mathbf{k}}_t^{\top }\\ & ={\mathbf{S}}_{t-1}-({\mathbf{S}}_{t-1}{\mathbf{k}}_t){\mathbf{k}}_t^{\top }+{\mathbf{v}}_t{\mathbf{k}}_t^{\top }\\ & ={\mathbf{S}}_{t-1}(\mathbf{I}-{\mathbf{k}}_t{\mathbf{k}}_t^{\top })+{\mathbf{v}}_t{\mathbf{k}}_t^{\top }\end{array}$$

相比于一开始的状态更新，DeltaNet的状态更新之前先减去了一个 $(S_{t-1}{k}_t)k_t^T$，$S_{t-1}{k}_t$是模型对$v$的预测，所以这里就有点像是 去除模型的旧知识，加入正确的新知识。这个规则称为Delta Rule，也是Delta的来源

关于DeltaNet，原作者Sonta也写了比较详细的博客 DeltaNet Explained (Part I) | Songlin Yang

Training

原本打算独立开一个训练部分，但是苏神这里提到了DeltaNet高效训练的处理，这里也就顺带记一下
Transformer-based 虽然推理效率不高，时空间复杂度都是$O(n^2)$，但是训练时大体上是并行的，也就意味着训练的效率并不低
RNN-based并不天生适合并行训练，需要找到某种方法来实现并行，幸运的是这些方法并不是很难找/有人已经找到了。苏神这里提到并行化的通解是 转化为 Prefix Sum然后Associative Scan

稍微具体一点地说，通解的(一个)做法是将问题变成广义的prefix sum问题，后面状态$h_k$的计算与前面状态$h_i$的计算存在线性关系(某个满足结合律的运算)，由于结合律存在，前缀和计算可以转换成并行的计算，即发现可以不断二分成两部分计算，递归下去可以将$O(n)$的复杂度变成$O(log(n))$
例如在苏神另一篇文章 Google新作试图“复活”RNN：RNN能否再次辉煌？ - 科学空间|Scientific Spaces 中提到的一个例子，每个时间步的计算可以拆分成两个部分，第二部分由自身的运算和第一部分的末尾结果得到，进一步二分可以得到图右的递归树，时间复杂度就从$O(L)$ 变成 $O(log(L))$

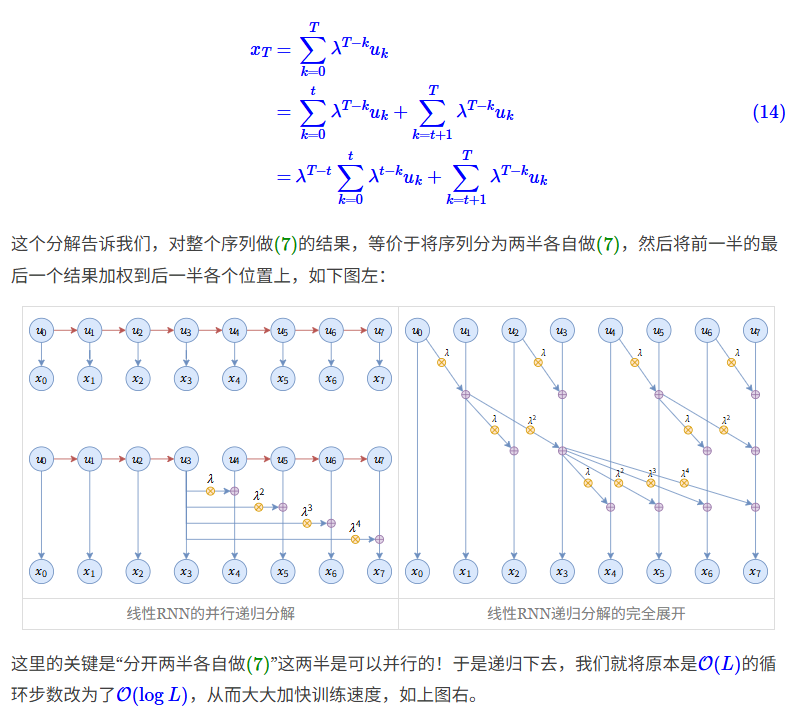
但是通解并不是一个GPU高效的做法，GPU擅长矩阵乘法，更高效的做法应该是引入尽可能多的矩阵乘法来进行训练
以DeltaNet为例，我们尝试为其引入更多的矩阵运算
原计算为

$${\mathbf{S}}_t={\mathbf{S}}_{t-1}-{\eta }_t({\mathbf{S}}_{t-1}{\mathbf{k}}_t-{\mathbf{v}}_t){\mathbf{k}}_t^{\top }$$

同样的，由于${\eta }_t$是常数，直接设为1(可以认为是被吸收了也可以在之后补回来)
将式子改写为

$${\mathbf{S}}_t={\mathbf{S}}_{t-1}+({\mathbf{v}}_{\mathbf{t}}-{\mathbf{S}}_{t-1}{\mathbf{k}}_t){\mathbf{k}}_t^{\top }$$

将${\mathbf{v}}_{\mathbf{t}}-{\mathbf{S}}_{t-1}{\mathbf{k}}_t$ 记作 ${\mathbf{u}}_{\mathbf{t}}$，原式就可以改写成 ${\mathbf{S}}_t={\mathbf{S}}_{t-1}+{\mathbf{u}}_t{\mathbf{k}}_t^{\top }$ (与原线性注意力形式相同)，$S_t$就可以写为 ${\mathbf{S}}_{t-1}={\sum }_{j=1}^{t-1}{\mathbf{u}}_j{\mathbf{k}}_j^{\top }$ 给定任意时间点$t$，可以得到

$${\mathbf{u}}_t={\mathbf{v}}_t-\left(\sum _{j=1}^{t-1}{\mathbf{u}}_j{\mathbf{k}}_j^{\top }\right){\mathbf{k}}_t={\mathbf{v}}_t-\sum _{j=1}^{t-1}{\mathbf{u}}_j({\mathbf{k}}_j^{\top }{\mathbf{k}}_t)$$

我们希望出现矩阵，记$\mathbf{U}=[{\mathbf{u}}_1,{\mathbf{u}}_2,\cdots ,{\mathbf{u}}_n{]}^{\top }$，将这个式子改写成对应的矩阵形式

$$\mathbf{U}=\mathbf{V}-(\mathbf{K}{\mathbf{K}}^{\top }\odot {\mathbf{M}}^{-})\mathbf{U}$$

其中$M^{-}$ 是$M-I$，$M$与$\odot$与上面的定义相同。$K{K}^T$计算得到的是$k_i^T{k}_j$，虽然与上式形式不同但结果相同，与$M^{-}$的逐元素积得到一个缺少主对角线的下三角阵，对应上式中的$t-1$
我们需要算出$U$，即可以通过矩阵的方式并行得到每个时间步的状态，如果将上式当成线性方程求解，需要计算 $(I+K{K}^T\odot M^{-})$ 的逆，时间复杂度为$O(n^3)$，并不可取。DeltaNet的做法是改成求解方程组$(I+K{K}^T\odot M^{-})U=V$，再利用矩阵特性将复杂度降到线性然后分块求解

待细看DeltaNet

DeltaNet为例，将线性注意力的状态更新改写回矩阵的形式是一种利用GPU做并行的方法，这实际上也暴露了线性注意力的一些问题，尽管其形式上是线性的，但是在进行矩阵化/并行的时候不一定能轻松得到线性的复杂度

Gated DeltaNet

Gated DeltaNet将遗忘门加入到了DeltaNet中，它的引入方式为

$${\mathbf{S}}_t={\alpha }_t{\mathbf{S}}_{t-1}\left(\mathbf{I}-{\beta }_t{\mathbf{k}}_t{\mathbf{k}}_t^{\top }\right)+{\beta }_t{\mathbf{v}}_t{\mathbf{k}}_t^{\top }$$

这样的做法拆开的话是这样的

$${\mathbf{S}}_t={\alpha }_t{\mathbf{S}}_{t-1}-{\alpha }_t{\mathbf{S}}_{t-1}{\beta }_t{\mathbf{k}}_t{\mathbf{k}}_t^{\top }+{\beta }_t{\mathbf{v}}_t{\mathbf{k}}_t^{\top }$$

这里有什么问题呢？这里的做法给第二个$S_{t-1}$也乘上了衰减因子，也给新旧知识的计算乘上了因子，按照Delta Rule，这应该是旧知识的refine，这两个地方的衰减因子不是很有道理

当然为了前后一致也合理

苏神认为比较好的是来自Comba的做法，只对第一个状态做衰减

$${\mathbf{S}}_t={\gamma }_t{\mathbf{S}}_{t-1}+{\eta }_t\left({\mathbf{v}}_t-{\mathbf{S}}_{t-1}{\mathbf{k}}_t\right){\mathbf{k}}_t^{\top }$$

二者可以是等价的(衰减因子可被吸收)，说${\alpha }_t$多数接近于1，能力应当差别不大
后者确实数学形式优雅一点

这里就必须补充一些不太相关的内容 搜索的时候发现Linear Attention的几位大佬进行了争辩/骂战；内容大概是 DeltaNet 的溯源(来自jürgen schmidhuber，LSTM之父) + 一些与RWKV设计的“雷同”？
有必要进一步了解论文

核技巧

这个并不是按时间顺序书写的，核技巧在很早就出现在linear attention或linear RNN中

核技巧最常见的是用于SVM，SVM中，我们希望将当前维度线性不可分的问题通过映射函数$\varphi$投影到高维空间使得线性可分，但是高维向量的计算过于昂贵，我们将损失转换成对偶问题，得到内积形式，通过核函数计算高维函数的内积
即

$$\mathbf{k}(\mathbf{x},\mathbf{y})\approx \mathbf{\varphi }(\mathbf{x}{)}^{\top }\mathbf{\varphi }(\mathbf{y})$$

在Linear Attention中，核技巧的思路是反过来的，给定核函数$exp()$，我们希望找到一个映射函数 $\varphi ()$，使得线性注意力的计算近似于softmax attention

$$\exp ({\mathbf{q}}_i^{\top }{\mathbf{k}}_j)\approx \mathbf{\varphi }({\mathbf{q}}_i{)}^{\top }\mathbf{\varphi }({\mathbf{k}}_j)$$

这样除了让linear Attention接近于Softmax Attention之外(不一定需要，各有优势)，还可以让二者联系起来，一些在Linear Attention的改进可以(近似)拿到Softmax Attention中，所以苏神这里主要讨论的是 Linear Attention对Softmax Attention的反哺

我们列出上述Attention的矩阵形式

Softmax Attention	$\left(\exp \left(\mathbf{Q}{\mathbf{K}}^{\top }\right)\odot \mathbf{M}\right)\mathbf{V}$
最早的线性Attention	$\left(\mathbf{Q}{\mathbf{K}}^{\top }\odot \mathbf{M}\right)\mathbf{V}$
加入遗忘门后	$\left(\mathbf{Q}{\mathbf{K}}^{\top }\odot \mathbf{\Gamma }\right)\mathbf{V}$
DeltaNet	$\left(\mathbf{Q}{\mathbf{K}}^{\top }\odot \mathbf{M}\right){\left(\mathbf{I}+\mathbf{K}{\mathbf{K}}^{\top }\odot {\mathbf{M}}^{-1}\right)}^{-1}\mathbf{V}$
Gated DeltaNet	$\begin{array}{rl}& \left(\left(\mathbf{Q}{\mathbf{K}}^{\top }\odot \mathbf{M}\right){\left(\mathbf{I}+\mathbf{K}{\mathbf{K}}^{\top }\odot {\mathbf{M}}^{-1}\right)}^{-1}\odot \mathbf{\Gamma }\right)\mathbf{V}\\ & =\left(\mathbf{Q}{\mathbf{K}}^{\top }\odot \mathbf{\Gamma }\right){\left(\mathbf{I}+\mathbf{K}{\mathbf{K}}^{\top }\odot {\mathbf{\Gamma }}^{-1}\right)}^{-1}\mathbf{V}\end{array}$

其中

$${\mathbf{\Gamma }}_{i,j}=\{\begin{array}{ll}\prod _{\tau =j+1}^i{\mathbf{\gamma }}_{\tau },& i>j\\ 1,& i=j\\ 0,& i<j\end{array}$$

可以看到除了exp之外，Softmax Attention的形式相比于Linear Attention来说是比较简单的，或者说Linear Attention正在发展Attention的计算形式，通过映射函数可以将这些优化恢复到Softmax Attention中

苏神给出了ALIBI和FoX的例子，确实是巧妙的角度，但是论文原本的思路可能更直觉，这里就暂时不提

一个比较有意思的是苏神提到的DeltaFormer，这篇工作提出了DelatNet形式的Softmax Attention

$$\begin{array}{rl}& \left(\mathbf{\varphi }(\mathbf{Q})\mathbf{\varphi }(\mathbf{K}{)}^{\top }\odot \mathbf{M}\right){\left(\mathbf{I}+\mathbf{\varphi }(\mathbf{K})\mathbf{\varphi }(\mathbf{K}{)}^{\top }\odot {\mathbf{M}}^{-1}\right)}^{-1}\mathbf{V}\\ & =\underset{\text{记为}\mathbf{A}}{\underbrace{\exp (\mathbf{Q}{\mathbf{K}}^{\top }+\log \mathbf{M})}}{\left(\mathbf{I}+\underset{\text{记为}\mathbf{B}}{\underbrace{\exp (\mathbf{K}{\mathbf{K}}^{\top }+\log {\mathbf{M}}^{-1}))}}\right)}^{-1}\mathbf{V}\end{array}$$

相比起原本的Softmax Attention，DeltaFormer改变(不一定是改进)了注意力的计算，也就是引入了来自Linear Attention的反哺，原本的计算是 $AV$，DeltaFormer变成 $A(I+B{)}^{-1}V$
根据诺伊曼级数，将矩阵的逆展开可以得到

$$\begin{array}{rl}\mathbf{A}(\mathbf{I}+\mathbf{B}{)}^{-1}\mathbf{V}& =\mathbf{A}(\mathbf{I}-\mathbf{B}+{\mathbf{B}}^2-{\mathbf{B}}^3+\cdots )\mathbf{V}\\ & =\mathbf{A}(\mathbf{V}-\mathbf{B}\mathbf{V}+{\mathbf{B}}^2\mathbf{V}-{\mathbf{B}}^3\mathbf{V}+\cdots )\end{array}$$

注意力的计算就变成多次迭代计算KKV的得到综合的V，每次都是KK相似度计算一次attention得到新的V，每个位置的v在一次计算之后会根据它与前面位置的相似度更新，这种更新会在下一次计算的时候传递给其它位置，例如说B在第一次更新根据BA关系获得了A的信息，C在此次更新根据CB，CA关系获得了A,B信息，在下一次更新的时候，BA关系就传递给了C，然后最终得到的V再与原QK得到最终的attention。这样的计算对multi-hop问题有奇效
只不过在实际实验的时候损失与原本相差无几，在一方面的提升可能带来了另一方面的损失

Note

诺伊曼级数(Neumann series)是一种矩阵级数，常用于求矩阵的逆。满足如果诺伊曼级数收敛，矩阵$(I-T)$可逆

$$(\mathbf{I}-\mathbf{T}{)}^{-1}=\sum _{k=0}^{\infty }{\mathbf{T}}^k$$

通过将矩阵A转换成 $I-(I-A)$就可以利用级数计算A的逆 它的证明很简单

$$\underset{n\to \infty }{\lim }(\mathbf{I}-\mathbf{T}){\mathbf{S}}_n=\underset{n\to \infty }{\lim }\left(\sum _{k=0}^n{\mathbf{T}}^k-\sum _{k=0}^n{\mathbf{T}}^{k+1}\right)=\underset{n\to \infty }{\lim }(\mathbf{I}-{\mathbf{T}}^{n+1})=\mathbf{I}$$

在这里用它来分解矩阵的逆

Position Encoding

除了用线性注意力的注意力计算方式改进Softmax Attention，我们还可以用线性注意力天然的上下文相关位置特性反哺Softmax Attention，也就是把线性注意力的特性引入Softmax Attention的位置编码中

一份相关的硬核工作是PaTH
首先，任何的正交矩阵$\Omega$的幂$R_m={\Omega }^m$ 都可以构成广义的RoPE。一个常见的正交矩阵是Householder矩阵(镜面反射)：满足$w$是任意模长为$\sqrt{2}$的列向量，则$I-w{w}^T$为正交矩阵

巧合的是这个矩阵的形式与DeltaNet状态更新中 $I-k_t{k}_t^T$ 是一样的，PaTH进一步舍弃了正交矩阵的幂和向量长度的约束，采用了形似但是更加灵活的做法

$${\mathbf{q}}_i^{\top }{\mathbf{k}}_j\to {\mathbf{q}}_i^{\top }\underset{\text{记为}{\mathbf{R}}_{i,j}}{\underbrace{(\mathbf{I}-{\mathbf{w}}_i{\mathbf{w}}_i^{\top })(\mathbf{I}-{\mathbf{w}}_{i-1}{\mathbf{w}}_{i-1}^{\top })\cdots (\mathbf{I}-{\mathbf{w}}_{j+1}{\mathbf{w}}_{j+1}^{\top })}}{\mathbf{k}}_j$$

注意这里，$i>j$，$R_{ij}$的递归形式是${\mathbf{R}}_{i,j}=\left(\mathbf{I}-{\mathbf{w}}_i{\mathbf{w}}_i^{\top }\right){\mathbf{R}}_{i-1,j},{\mathbf{R}}_{j,j}=\mathbf{I}$

我们需要得到一个Softmax Attention的形式，或者说矩阵形式方便并行训练和对Softmax Attention进行改进
将$R_{ij}$写成矩阵形式

$${\mathbf{R}}_{i,j}=\mathbf{I}-{\mathbf{W}}_{[j:i]}^{\top }{\left(\mathbf{I}+{\mathbf{W}}_{[j:i]}{\mathbf{W}}_{[j:i]}^{\top }\odot {\mathbf{M}}^{-}\right)}^{-1}{\mathbf{W}}_{[j:i]}$$

其中$\mathbf{W}={\left[{\mathbf{w}}_1,{\mathbf{w}}_2,\cdots ,{\mathbf{w}}_n\right]}^{\top }$，索引的方式与python索引一致，先切片再转置
然后由于$M^{-}$和加$I$，$W^T,W$中间的矩阵是一个下三角阵，它属于一个完整的下三角阵的对角块
所以有

$${\left(\mathbf{I}+{\mathbf{W}}_{[j:i]}{\mathbf{W}}_{[j:i]}^{\top }\odot {\mathbf{M}}^{-}\right)}^{-1}=(\underset{\text{记为}\mathbf{J}}{\underbrace{{\left(\mathbf{I}+\mathbf{W}{\mathbf{W}}^{\top }\odot {\mathbf{M}}^{-}\right)}^{-1}}}{)}_{[j:i,j:i]}$$

然后，我们来计算整个注意力矩阵

$$\begin{array}{rl}{A}_{i,j}& ={\mathbf{q}}_i^{\top }{\mathbf{R}}_{i,j}{\mathbf{k}}_j\\ & ={\mathbf{q}}_i^{\top }{\mathbf{k}}_j-{\mathbf{q}}_i^{\top }{\mathbf{W}}_{[j:i]}^{\top }{\mathbf{J}}_{[j:i,j:i]}{\mathbf{W}}_{[j:i]}{\mathbf{k}}_j\\ & ={\mathbf{q}}_i^{\top }{\mathbf{k}}_j-\sum _{p=1}^d\sum _{l=j+1}^i\sum _{r=j+1}^i\sum _{s=1}^d{Q}_{i,p}{W}_{l,p}{J}_{l,r}{W}_{r,s}{K}_{j,s}\\ & ={\mathbf{q}}_i^{\top }{\mathbf{k}}_j-\sum _{p=1}^d\sum _{l=1}^i\sum _{r=j+1}^n\sum _{s=1}^d{Q}_{i,p}{W}_{l,p}{J}_{l,r}{W}_{r,s}{K}_{j,s}\\ & ={\mathbf{q}}_i^{\top }{\mathbf{k}}_j-\sum _{p=1}^d\sum _{l=1}^n\sum _{r=1}^n\sum _{s=1}^d{Q}_{i,p}{W}_{l,p}{\chi }_{l\le i}{J}_{l,r}{\chi }_{r\ge j+1}{W}_{r,s}{K}_{j,s}\\ & ={\mathbf{q}}_i^{\top }{\mathbf{k}}_j-\sum _{l=1}^n\sum _{r=1}^n\underset{{\mathbf{QW}}^{\top }\odot \mathbf{M}}{\underbrace{\left({\chi }_{l\le i}\sum _{p=1}^d{Q}_{i,p}{W}_{l,p}\right)}}{J}_{l,r}\underset{{\mathbf{WK}}^{\top }\odot {\mathbf{M}}^{-}}{\underbrace{\left({\chi }_{r\ge j+1}\sum _{s=1}^d{W}_{r,s}{K}_{j,s}\right)}}\end{array}$$

先从单个位置出发得到算式，逐渐将算式通过下三角($j>r$的地方为0所以写进来没问题)，指示函数(满足条件才为1)将矩阵扩大到完整的矩阵$Q,W,K$中，最终得到注意力矩阵 A

$$\mathbf{A}=\mathbf{Q}{\mathbf{K}}^{\top }\odot \mathbf{M}-(\mathbf{Q}{\mathbf{W}}^{\top }\odot \mathbf{M})(\mathbf{I}+\mathbf{W}{\mathbf{W}}^{\top }\odot {\mathbf{M}}^{-}{)}^{-1}(\mathbf{W}{\mathbf{K}}^{\top }\odot {\mathbf{M}}^{-})$$

然后求逆的话需要$O(n^3)$，所以同样利用下三角+低秩等特点进行简化得到最后的计算

PaTH的位置编码并不像RoPE等位置编码一样对位置本身进行编码(忽视位置之外的信息)，而是会考虑上下文的内容进行位置编码，属于 CoPE(Contextual Position Encoding)

PaTH与DeltaNet的关系

PaTH的注意力矩阵是

$$\mathbf{A}=\mathbf{Q}{\mathbf{K}}^{\top }\odot \mathbf{M}-(\mathbf{Q}{\mathbf{W}}^{\top }\odot \mathbf{M})(\mathbf{I}+\mathbf{W}{\mathbf{W}}^{\top }\odot {\mathbf{M}}^{-}{)}^{-1}(\mathbf{W}{\mathbf{K}}^{\top }\odot {\mathbf{M}}^{-})$$

提取出$\mathbf{Q}{\mathbf{K}}^{\top }\odot \mathbf{M}$ 得到

$$\mathbf{A}=(\mathbf{Q}{\mathbf{K}}^{\top }\odot \mathbf{M})(\mathbf{I}-(\mathbf{I}+\mathbf{W}{\mathbf{W}}^{\top }\odot {\mathbf{M}}^{-}{)}^{-1}(\mathbf{W}{\mathbf{K}}^{\top }\odot {\mathbf{M}}^{-})$$

如果$W=K$，则得到

$$\begin{array}{rl}\mathbf{A}& =(\mathbf{Q}{\mathbf{K}}^{\top }\odot \mathbf{M})(\mathbf{I}-(\mathbf{I}+\mathbf{K}{\mathbf{K}}^{\top }\odot {\mathbf{M}}^{-1}{)}^{-1}(\mathbf{K}{\mathbf{K}}^{\top }\odot {\mathbf{M}}^{-1}))\\ & =(\mathbf{Q}{\mathbf{K}}^{\top }\odot \mathbf{M})(\mathbf{I}+\mathbf{K}{\mathbf{K}}^{\top }\odot {\mathbf{M}}^{-1}{)}^{-1}\end{array}$$

$\mathbf{I}-(\mathbf{I}+\mathbf{A}{)}^{-1}\mathbf{A}=(\mathbf{I}+\mathbf{A}{)}^{-1}$ ，左右两边乘以$(I+A)$ 得证

可以看到$W=K$ 的特例下，DeltaNet与PaTH的注意力计算是一致的，同样使用DeltaNet的注意力计算的还有DeltaFormer。DeltaFormer和PaTH的区别在于一个使用核技巧，一个是直接的softmax

然后苏神还提供了另一个角度
如果引入对$w$的L2范数约束，可以把$R_{ij}$变成RoPE，我们可以从这个角度看看PaTH的位置编码方式
RoPE对qk进行编码，以q为例

$$\begin{array}{rl}({\mathbf{q}}_i^{\top }{\mathbf{R}}_i{)}_s& =({\mathbf{q}}_i^{\top }-{\mathbf{q}}_i^{\top }{\mathbf{W}}_{[:i]}^{\top }{\mathbf{J}}_{[:i,:i]}{\mathbf{W}}_{[:i]}{)}_s\\ & =Q_{i,s}-\sum _{p=1}^d\sum _{l=1}^i\sum _{r=1}^i{Q}_{i,p}{W}_{l,p}{J}_{l,r}{W}_{r,s}\\ & =Q_{i,s}-\sum _{p=1}^d\sum _{l=1}^i\sum _{r=1}^n{Q}_{i,p}{W}_{l,p}{J}_{l,r}{W}_{r,s}\\ & =Q_{i,s}-\sum _{p=1}^d\sum _{l=1}^n\sum _{r=1}^n{\chi }_{l\le i}{Q}_{i,p}{W}_{l,p}{J}_{l,r}{W}_{r,s}\\ & =Q_{i,s}-\sum _{l=1}^n{\chi }_{l\le i}\underset{\mathbf{Q}{\mathbf{W}}^{\top }\odot \mathbf{M}}{\underbrace{\sum _{p=1}^d{Q}_{i,p}{W}_{l,p}}}\underset{\mathbf{J}\mathbf{W}}{\underbrace{\sum _{r=1}^n{J}_{l,r}{W}_{r,s}}}\end{array}$$

矩阵形式是

$$\mathbf{Q}-(\mathbf{Q}{\mathbf{W}}^{\top }\odot \mathbf{M})(\mathbf{I}+\mathbf{W}{\mathbf{W}}^{\top }\odot {\mathbf{M}}^{-}{)}^{-1}\mathbf{W}$$

也就是Q减去 $\mathrm{DeltaNet}(\mathrm{Q},\mathrm{W},\mathrm{W})$，对K也同理，也就是说PaTH此时的位置编码就是使用DeltaNet给QK进行编码

$$\text{SoftmaxAttention}(\underset{\bar{\mathbf{Q}}}{\underbrace{\mathbf{Q}-\text{DeltaNet}(\mathbf{Q},\mathbf{W},\mathbf{W})}},\underset{\bar{\mathbf{K}}}{\underbrace{\mathbf{K}-\text{DeltaNet}(\mathbf{K},\mathbf{W},\mathbf{W})}},\mathbf{V})$$

MesaNet

从TTT的角度来看，DeltaNet是使用SGD优化目标函数$\frac{1}{2}\Vert \mathbf{S}\mathbf{k}-\mathbf{v}{\Vert }^2$，由于参数计算只涉及到$Sk$这样的线性变换，这是一个经典的线性回归问题，可以求出解析解

给定一个形如 $||SX-y|{|}^2$为目标函数的线性回归问题，我们可以求出其解析解
将损失以矩阵形式展开，$(SX-y{)}^T(SX-y)=(SX{)}^T(SX)-(SX{)}^{T}y-y^T(SX)+y^{T}y$
对参数$S$求导得到 $2SX{X}^T-2X^{T}y$
令导数为0得到

$$S=X^{T}y(X{X}^T{)}^{-1}$$

在DeltaNet这里，$y=v,k=X$，所以有

$${\mathbf{S}}_t={\mathbf{G}}_t{\mathbf{H}}_t^{-1},{\mathbf{G}}_t=\sum _{j=1}^t{\mathbf{v}}_j{\mathbf{k}}_j^{\top },{\mathbf{H}}_t=\sum _{j=1}^t{\mathbf{k}}_j{\mathbf{k}}_j^{\top }$$

给出了解析解，可以拿掉TTT框架对$S_t$的状态修改，直接使用解析解更新状态

$${\mathbf{o}}_t={\mathbf{G}}_t({\mathbf{H}}_t{)}^{-1}{\mathbf{q}}_t,{\mathbf{G}}_t={\mathbf{G}}_{t-1}+{\mathbf{v}}_t{\mathbf{k}}_t^{\top },{\mathbf{H}}_t={\mathbf{H}}_{t-1}+{\mathbf{k}}_t{\mathbf{k}}_t^{\top }$$

MesaNet进一步加入了遗忘门和对角阵(避免不可逆)

$${\mathbf{o}}_t={\mathbf{G}}_t({\mathbf{H}}_t+{\mathbf{\Lambda }}_t{)}^{-1}{\mathbf{q}}_t,{\mathbf{G}}_t={\gamma }_t{\mathbf{G}}_{t-1}+{\mathbf{v}}_t{\mathbf{k}}_t^{\top },{\mathbf{H}}_t={\gamma }_t{\mathbf{H}}_{t-1}+{\mathbf{k}}_t{\mathbf{k}}_t^{\top }$$

理论上看，MesaNet数学形式很优雅
MesaNet是一个解析解形式的Attention，解析解的目标是记忆$k,v$，这样的做法使得MesaNet的能力起点优于DeltaNet，但并非所有k,v都相同重要，Delta Rule带来的灵活性可能能使DeltaNet优于MesaNet
也因为MesaNet是解析解，自己的发展可能也就到此为止，稍作改动可能就无法再得到解析解形式
实践上看，求逆问题的复杂度会是MesaNet的一大优化难点

DeltaNet

DeltaNet专题
DeltaNet应该是记录这篇笔记的时候比较受欢迎的架构(主要是Gated DeltaNet)，Qwen，Kimi先后推出了使用Gated DeltaNet的混合架构

DeltaNet Details

让我们先从论文[2406.06484] Parallelizing Linear Transformers with the Delta Rule over Sequence Length作者Songlin Yang的博客中看一些架构细节

FROM

• DeltaNet Explained (Part I) | Songlin Yang
• DeltaNet Explained (Part II) | Songlin Yang
• DeltaNet Explained (Part III) | Songlin Yang

The Model

我们已知 Linear Attention 最简单的做法就是直接将exp去掉

$${\mathbf{o}}_t={\mathbf{S}}_t{\mathbf{q}}_t,{\mathbf{S}}_t={\mathbf{S}}_{t-1}+{\mathbf{v}}_t{\mathbf{k}}_t^{\top }$$

上下文信息存储在状态$S_t$中，它是一个 $v_t,k_t$ 外积的和，这样的形式(fixed size与sum)虽然cover了所有信息，但是对信息的还原是不精确的
如果希望提取出位置j对应的value，我们会得到

$$\begin{array}{rl}\mathbf{S}{\mathbf{k}}_j& =\sum {\mathbf{v}}_i({\mathbf{k}}_i^{\top }{\mathbf{k}}_j)\\ & ={\mathbf{v}}_j+\underset{\text{retrieval error}}{\underbrace{\sum _{i\ne j}({\mathbf{k}}_i^{\top }{\mathbf{k}}_j){\mathbf{v}}_i}}\end{array}$$

为了精确地decode信息，我们需要$k_i^T{k}_j$部分为0，也就是不同位置的key内积为0，即正交。遗憾的是给定d维空间($S_t$)，只能找到d个正交的向量，也就是一旦token数量超过d，存储就会是有损的。同时提高head dimension能够提高performance

好证明！

所以DeltaNet认为，之所以linear attention 不如 softmax attention，是因为linear attention并不能erase existing memories

关于这一点我并不很理解，然后通过与AI争辩得到了一个大概的说法
疑惑点在哪呢？大概有两个

• 从状态中恢复出key value pair和模型表现有什么关系，
• 为什么linear attention只是改变了attention的计算顺序，不考虑softmax计算是等价的，却突然出现了状态无法记忆上下文的情况

两个问题实际上是一件事，我们改变了计算顺序，通过存储State来计算attention，在数学上是等价的(与不考虑softmax的standard attention相比)，产生了因为softmax运算带来的性能下降很合理，为什么会出现无法存储信息带来的性能下降？ 我认为，Attention中，query的作用是筛选key，通过对key的筛选来筛选value，如果我直接输入key(把key当query)，我们希望能够得到key对应的value。对于linear attention，$Sk$无法得到value，确实可以看成是一种信息的丢失。

我们先更进一步的看看这种信息丢失
首先在原本的计算中，我们是每一次都重建KV进行计算的，也就是

$$O=(Q{K}^T\odot M)V$$

我们重建了KV，也就意味着没有恢复的问题，同时完整的KV参与了计算，此时的信息量(只考虑KV的话)是$O(2nd)$
当我们使用streaming的方式/recurrent的方式，即存储状态 $S$ 的时候，计算是

$$o_t=S_t{q}_t$$

此时KV信息存储在S中，维度变成 $O(d^2)$，当n大于d的时候，出现了信息的丢失
从另一个角度来看，定义函数

$$\mathcal{F}:(V,K)\to S$$

给定不同的KV，是可以得到相同的S的，也就是说函数并不是单射，函数不可逆
也就是说，通过改变计算+使用streaming的方式，在信息的角度产生了信息丢失

看上去很有道理，似乎直接指向了性能下降，但是从结果来看，二者数学上仍然是等价的，无论你怎么说，一定满足

$${\mathbf{o}}_t=\sum _{j=1}^t{\mathbf{v}}_j({\mathbf{k}}_j^{\top }{\mathbf{q}}_t)=\sum _{j=1}^t({\mathbf{v}}_j{\mathbf{k}}_j^{\top }){\mathbf{q}}_t=\left(\sum _{j=1}^t{\mathbf{v}}_j{\mathbf{k}}_j^{\top }\right){\mathbf{q}}_t={\mathbf{S}}_{\mathbf{t}}{\mathbf{q}}_t$$

所以这个信息损失究竟体现在哪里
现在的我认为，这个信息丢失必须考虑softmax才是有效的，我们丢失了distinct的KV信息，这个信息支撑了softmax对上下文的信息的动态筛选，也就是删去无关的KV，保留相关的KV
softmax强化了query对KV的筛选，它能够彻底删去一些kv对当前计算产生的影响，而没有softmax的attention无法做到，所以每次计算注意力都进行KV重建，这个信息重点在于提供给softmax动态筛选的能力
所以重点在动态筛选记忆(不知道对不对)
DeltaNet 则是从另一个角度来进行记忆筛选

这个角度是Delta Rule: (An error-correction principle)通过diff来调整模型的参数

$$\begin{array}{rl}{\mathbf{S}}_t& ={\mathbf{S}}_{t-1}-{\beta }_t({\mathbf{S}}_{t-1}{\mathbf{k}}_t-{\mathbf{v}}_t){\mathbf{k}}_t^{\top }\\ & ={\mathbf{S}}_{t-1}-{\beta }_t{\mathbf{S}}_{t-1}{\mathbf{k}}_t{\mathbf{k}}_t^{\top }+{\beta }_t{\mathbf{v}}_t{\mathbf{k}}_t^{\top }\end{array}$$

博客使用$\beta$ 表示learning rate
实际上Delta Rule的理念与 Gradient Descent 十分接近，很自然就会考虑当前的 diff 是什么函数的梯度

通过简单实验作者发现 DeltaNet is good at in-context retrieval tasks

Note

在这里补充两个benchmark的信息
MQAR benchmark是一种上下文召回率评估benchmark，多次查询随机生成(无法记忆)的映射关系，希望模型从上下文信息中恢复映射

[关联段]
key1: value1
key2: value2
...
keyM: valueM
[查询段]
query1: 
query2: 
...
queryN:  ← 要求模型同时回忆多个value 

MAD是一个更全面的benchmark，分为Recall, Compression, Selective Copy, Fuzzy Recall, Memorization几个方面
DeltaNet在Recall 相关任务上甚至超过了Transformer

为什么DeltaNet会擅长 In-context retrieval的任务？
简单把召回任务理解成，给定query，模型能够从上下文中提取到精确信息的话，DeltaNet因为其状态更新实际上是 minimize MSE loss，所以可能因此在Recall 任务上表现出色。这也是作者的解释

我们总结一下这些内容
按照我们上面的说法，首先DeltaNet work，主要是在于其找到一种优雅的方式模拟了动态筛选，这种方式就是对记忆的Delta Rule，但很明显可以看到这样的筛选还是过于简单（无论如何受限于固定大小的空间和线性复杂度），后续通过引入Forget Gate进一步优化十分合理
其二是DeltaNet通过Delta Rule得到的优秀召回能力，简单实验来看这优于Transformer，这也就体现了一种反哺的可能性，可能也是因此才有将DeltaNet拿回softmax attention的尝试

The Algorithm

Parallel Scan Attempt

DeltaNet是一个纯RNN的模型，我们需要找到其适合的并行方式
作者的第一个尝试是 Parallel Scan，也就是上文提到的通解：找到一个满足结合律的operator，将状态更新转换成一个前缀和问题，然后并行计算

首先我们需要矩阵形式的状态更新表达式

$$\begin{array}{rl}{\mathbf{S}}_t& ={\mathbf{S}}_{t-1}-{\beta }_t({\mathbf{S}}_{t-1}{\mathbf{k}}_t-{\mathbf{v}}_t){\mathbf{k}}_t^{\top }\\ & ={\mathbf{S}}_{t-1}-{\beta }_t{\mathbf{S}}_{t-1}{\mathbf{k}}_t{\mathbf{k}}_t^{\top }+{\beta }_t{\mathbf{v}}_t{\mathbf{k}}_t^{\top }\\ & ={\mathbf{S}}_{t-1}(\mathbf{I}-{\beta }_t{\mathbf{k}}_t{\mathbf{k}}_t^{\top })+{\beta }_t{\mathbf{v}}_t{\mathbf{k}}_t^{\top }\end{array}$$

定义 $\mathbf{I}-{\beta }_t{\mathbf{k}}_t{\mathbf{k}}_t^{\top }$为 ${\mathbf{M}}_t$，${\beta }_t{\mathbf{v}}_t{\mathbf{k}}_t^{\top }$为${\mathbf{X}}_t$
我们得到

$${\mathbf{S}}_t={\mathbf{S}}_{t-1}{\mathbf{M}}_t+{\mathbf{X}}_t\in {\mathbb{R}}^{d\times d}$$

接下来我们定义一个满足结合律的计算
定义状态为

$${\mathbf{c}}_t=[{\mathbf{M}}_t,{\mathbf{X}}_t]=[\mathbf{I}-{\beta }_t{\mathbf{k}}_t{\mathbf{k}}_t^{\top },{\beta }_t{\mathbf{v}}_t{\mathbf{k}}_t^{\top }]$$

两个相邻状态间的运算为

$${\mathbf{c}}_i\bullet {\mathbf{c}}_j=[{\mathbf{M}}_i{\mathbf{M}}_j,{\mathbf{M}}_j{\mathbf{X}}_i+{\mathbf{X}}_j]$$

由于满足结合律，所以相邻也可以是前缀与后缀相邻
以此我们可以构造一棵二叉归约树

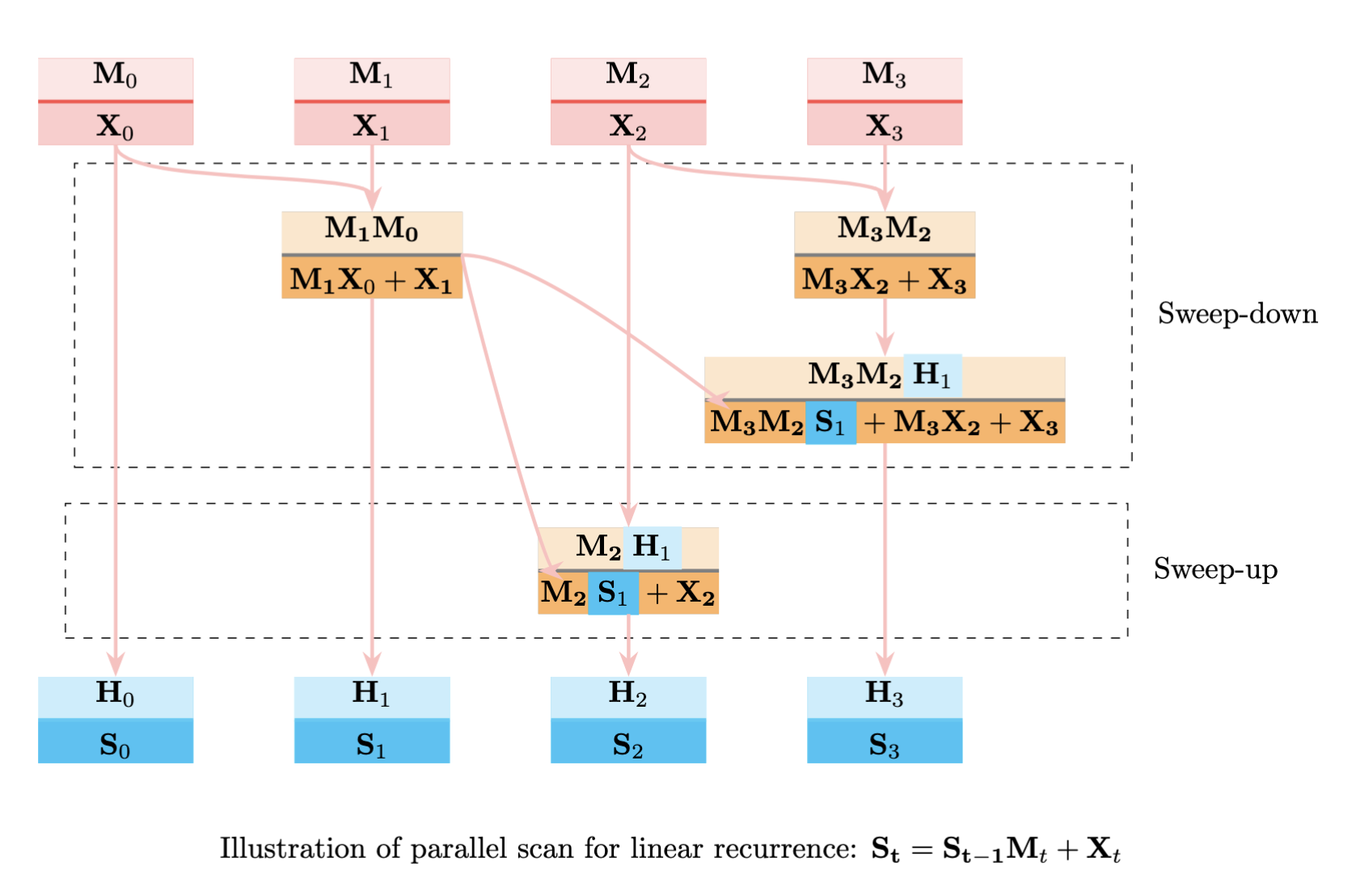
首先是归约(up-sweep)，树的叶子是上方的红色方块，是每个时刻对应的状态$c$，每一层是二叉两个子树的合，在这里树根为最右边的加和
至此这课二叉树每一层都是子树之和，而且每一层都可以并行计算，深度为 $O(logn)$
然后是分发(down-sweep)，我们最终需要得到的是每个时刻的前缀和，也就是上图蓝色部分
我们已经构建了形如下图的规约树

              root = b23 ⊕ b01
             /               \
        b01 (0,1)           b23 (2,3)
        /     \             /     \
      a0       a1         a2       a3

可以发现每个结点对应的前缀和，都可以通过自身与前缀的加和得到，左子树的前缀就是父节点的前缀，右子树的前缀就是父节点前缀与左子树的加和，我们可以同样递归处理这棵树直到所有叶子都得到结果，深度同样是 $O(logn)$

原博客提供的图有点奇怪，不知道是我理解错还是画错了，还是各个地方称呼不同，总之先归约求和再进行分配

尽管我们构建了二叉树，假设我们有无限的并行单元，每一层的计算都同时完成，时间应该就与$O(logn)$成正比，如果我们单纯考虑计算量，两棵树(归约和分发)都是二叉树，计算次数是除了叶子结点之外结点数量之和$L-1$，每次计算是$O(d^3)$(矩阵相乘)，所以复杂度应该是 $O(L{d}^3)$，由于我们的并行单元并不是无限的，所以仍然需要考虑实际的计算量。
原文写的是 $O(LLogL{d}^3)$，可能是一个保守的说法

这里看上去使用的parallel scan是Blelloch scan，如果是更早期的做法可能复杂度就是 $O(LLogL)$

时间复杂度主要问题在$d^3$，而除了时间复杂度外，空间复杂度也是问题。当前的做法(parallel scan)，中间矩阵需要$O(L{d}^2)$空间，同时由于parallel scan的约束(需要在后续步骤获取中间值)，我们需要一种方法，在不需要显式存储所有中间值的同时，降低当前的时间复杂度。切块(chunkwise — flash attention)的做法会是一个很自然的选择。

Chunkwise Algorithm

线性注意力的状态更新可以不显式存储中间的结果矩阵(当然为了快会存储)而只存储vector，向量外积之和可以通过临时矩阵的计算求得

$$\begin{array}{rl}\sum _{i=1}^t{\mathbf{v}}_i{\mathbf{k}}_i^{\top }& ={\mathbf{V}}_t{\mathbf{K}}_t^{\top }\\ \text{where }{\mathbf{V}}_t& =[{\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_t]\\ {\mathbf{K}}_t& =[{\mathbf{k}}_1,{\mathbf{k}}_2,\dots ,{\mathbf{k}}_t]\end{array}$$

拥有这样的性质，给定任意时刻t和对应的向量集$v_{1:t},k_{1:t}$，我们可以从任意先前时刻计算得到t时刻的状态，基于此我们就可以实现分块，我们可以只存储固定interval的中间状态矩阵，${\mathbf{S}}_0,{\mathbf{S}}_C,{\mathbf{S}}_{2C},\dots ,{\mathbf{S}}_{(n-1)C}\text{ where }\mathbf{n}=\lceil L/C\rceil$

符号规定如下

$$\begin{array}{rlr}& {\mathbf{S}}_{[i]}:={\mathbf{S}}_{iC}\in {\mathbb{R}}^{d\times d},{\square }_{[i]}={\square }_{iC+1:(i+1)C}\in {\mathbb{R}}^{C\times d}\text{ for }\square \in \{\mathbf{Q},\mathbf{K},\mathbf{V},\mathbf{O}\};& \\ & {\square }_{[i]}^r={\square }_{iC+r},\text{ for }\square \in \{\mathbf{q},\mathbf{k},\mathbf{v},\mathbf{o},\mathbf{s}\}.& \end{array}$$

也就是说，我们希望把Output的计算改写成矩阵形式的chunkwise运算，每个chunk的计算结果可以由该chunk对应的State和vectors求出
向量形式为

$$\begin{array}{rl}{\mathbf{S}}_{[i]}^r& ={\mathbf{S}}_{[i]}+\sum _{t=1}^r{\mathbf{v}}_{[i]}^t{\mathbf{k}}_{[i]}^{t\top }\\ {\mathbf{o}}_{[i]}^r& ={\mathbf{S}}_{[i]}^r{\mathbf{q}}_{[i]}^r={\mathbf{S}}_{[i]}{\mathbf{q}}_{[i]}^r+\sum _{t=1}^r{\mathbf{v}}_{[i]}^t\left({\mathbf{k}}_{[i]}^{t\top }{\mathbf{q}}_{[i]}^r\right)\end{array}$$

矩阵形式为

$$\begin{array}{rl}{\mathbf{S}}_{[t+1]}& ={\mathbf{S}}_{[t]}+{\mathbf{V}}_{[t]}^{\top }{\mathbf{K}}_{[t]}\in {\mathbb{R}}^{d\times d}\\ {\mathbf{O}}_{[t]}& ={\mathbf{Q}}_{[t]}{\mathbf{S}}_{[t]}^{\top }+({\mathbf{Q}}_{[t]}{\mathbf{K}}_{[t]}^{\top }\odot \mathbf{M}){\mathbf{V}}_{[t]}\in {\mathbb{R}}^{C\times d}\end{array}$$

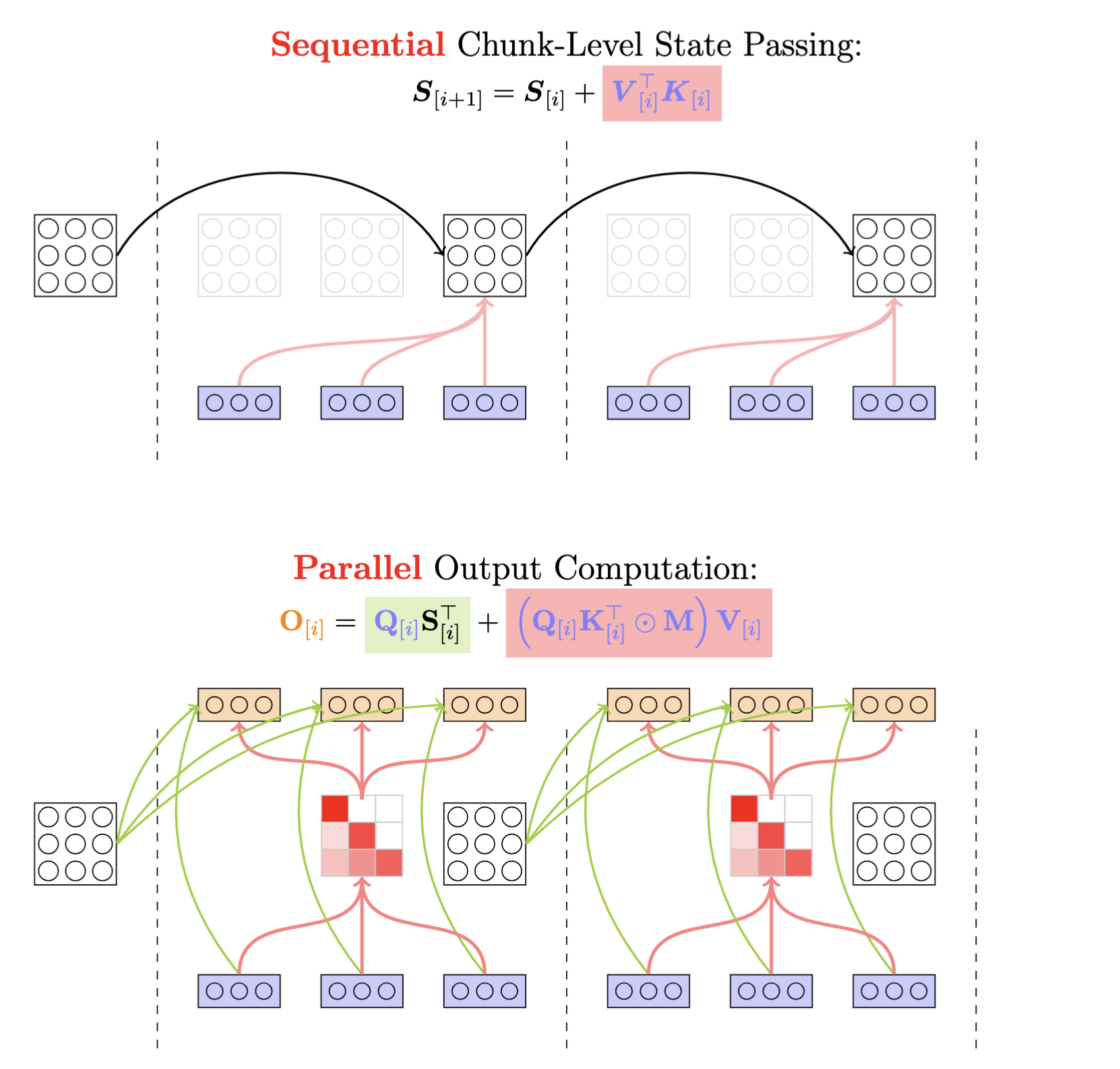
但是DeltaNet的状态转移比较复杂

$${\mathbf{S}}_t={\mathbf{S}}_{t-1}(\mathbf{I}-{\beta }_t{\mathbf{k}}_t{\mathbf{k}}_t^{\top })+{\beta }_t{\mathbf{v}}_t{\mathbf{k}}_t^{\top }$$

我们先根据线性注意力的做法得到块内的状态计算

$${\mathbf{S}}_{[i]}^r={\mathbf{S}}_{[i]}\prod _{t=1}^r\left(\mathbf{I}-{\beta }_{[i]}^t{\mathbf{k}}_{[i]}^t{\mathbf{k}}_{[i]}^{t\top }\right)+\sum _{t=1}^r\left({\beta }_{[i]}^t{\mathbf{v}}_{[i]}^t{\mathbf{k}}_{[i]}^{t\top }\prod _{s=t+1}^r\left(\mathbf{I}-{\beta }_{[i]}^s{\mathbf{k}}_{[i]}^s{\mathbf{k}}_{[i]}^{s\top }\right)\right)$$

由于$S_{t-1}(I-{\beta }_t{k}_t{k}_t^T)$ 的存在，任意两个时刻之间的转换需要计算第一部分，即左边的累乘(这个累乘没办法一口气算出)和第二部分，右边包含累乘的累加，一种可能的优化方向是尝试改写状态转移得到一个等价但是高效的计算形式
观察到 $(I-{\beta }_t{k}_t{k}_t^T)$ 接近于 Householder matrices，存在一种优雅的等价表示(WY representation）

$$\prod _{i=1}^t(\mathbf{I}-{\beta }_i{\mathbf{k}}_i{\mathbf{k}}_i^{\top })=\mathbf{I}-\sum _{i=1}^t{\mathbf{w}}_i{\mathbf{k}}_i^{\top }$$

可以通过归纳法简单证明

$$\begin{array}{rl}{\mathbf{P}}_n& ={\mathbf{P}}_{n-1}(\mathbf{I}-{\beta }_n{\mathbf{k}}_n{\mathbf{k}}_n^{\top })\\ & =\left(\mathbf{I}-\sum _{t=1}^{n-1}{\mathbf{w}}_t{\mathbf{k}}_t^{\top }\right)(\mathbf{I}-{\beta }_n{\mathbf{k}}_n{\mathbf{k}}_n^{\top })\\ & =\mathbf{I}-\sum _{t=1}^{n-1}{\mathbf{w}}_t{\mathbf{k}}_t^{\top }-{\beta }_n{\mathbf{k}}_n{\mathbf{k}}_n^{\top }+\left(\sum _{t=1}^{n-1}{\mathbf{w}}_t{\mathbf{k}}_t^{\top }\right){\beta }_n{\mathbf{k}}_n{\mathbf{k}}_n^{\top }\\ & =\mathbf{I}-\sum _{t=1}^{n-1}{\mathbf{w}}_t{\mathbf{k}}_t^{\top }-\underset{{\mathbf{w}}_n}{\underbrace{\left({\beta }_n{\mathbf{k}}_n-{\beta }_n\sum _{t=1}^{n-1}\left({\mathbf{w}}_t({\mathbf{k}}_t^{\top }{\mathbf{k}}_n)\right)\right)}}{\mathbf{k}}_n^{\top }\\ & =\mathbf{I}-\sum _{t=1}^n{\mathbf{w}}_t{\mathbf{k}}_t^{\top }\end{array}$$

可以看到中间过程给出了$w_t$的计算方法

但是状态转移累加部分同样不能通过这个新的形式一口气计算，观察到这部分实际上是拆开$S_{t-1}$逐渐得到的，如果将状态转移拆完，可以得到一个相同的形式

$$\begin{array}{rl}{\mathbf{S}}_t& ={\mathbf{S}}_{t-1}(\mathbf{I}-{\beta }_t{\mathbf{k}}_t{\mathbf{k}}_t^{\top })+{\beta }_t{\mathbf{v}}_t{\mathbf{k}}_t^{\top }\\ & =\sum _{i=1}^t{\beta }_i({\mathbf{v}}_i{\mathbf{k}}_i^{\top })\left(\prod _{j=i+1}^t(\mathbf{I}-{\beta }_j{\mathbf{k}}_j{\mathbf{k}}_j^{\top })\right)\end{array}$$

也就是说，第二部分实际上是一个块内的新状态计算，想要得到它的高效计算我们得从完整的状态计算入手
既然$(I-{\beta }_t{k}_t{k}_t^T)$ 可以看成是某种向量外积之和，那整个状态转移就可以也看成是某种向量外积之和，同样可通过归纳法证明

$$\begin{array}{rl}{\mathbf{S}}_n& ={\mathbf{S}}_{n-1}(\mathbf{I}-{\beta }_n{\mathbf{k}}_n{\mathbf{k}}_n^{\top })+{\beta }_n{\mathbf{v}}_n{\mathbf{k}}_n^{\top }\\ & =\left(\sum _{t=1}^{n-1}{\mathbf{u}}_t{\mathbf{k}}_t^{\top }\right)(\mathbf{I}-{\beta }_n{\mathbf{k}}_n{\mathbf{k}}_n^{\top })+{\beta }_n{\mathbf{v}}_n{\mathbf{k}}_n^{\top }\\ & =\sum _{t=1}^{n-1}{\mathbf{u}}_t{\mathbf{k}}_t^{\top }-\left(\sum _{t=1}^{n-1}{\mathbf{u}}_t{\mathbf{k}}_t^{\top }\right){\beta }_n{\mathbf{k}}_n{\mathbf{k}}_n^{\top }+{\beta }_n{\mathbf{v}}_n{\mathbf{k}}_n^{\top }\\ & =\sum _{t=1}^{n-1}{\mathbf{u}}_t{\mathbf{k}}_t^{\top }+\underset{{\mathbf{u}}_n}{\underbrace{\left({\beta }_n{\mathbf{v}}_n-{\beta }_n\sum _{t=1}^{n-1}{\mathbf{u}}_t({\mathbf{k}}_t^{\top }{\mathbf{k}}_n)\right)}}{\mathbf{k}}_n^{\top }\\ & =\sum _{t=1}^n{\mathbf{u}}_t{\mathbf{k}}_t^{\top }\end{array}$$

至此我们得到了一个通过向量外积一口气进行状态转移的计算形式

$$\begin{array}{rl}{\mathbf{S}}_{[i]}^r& ={\mathbf{S}}_{[i]}\underset{\text{chunk-local cumprod: }{\mathbf{P}}_{[i]}^r}{\underbrace{\prod _{t=1}^r\left(\mathbf{I}-{\beta }_{[i]}^t{\mathbf{k}}_{[i]}^t{\mathbf{k}}_{[i]}^{t\top }\right)}}+\underset{\text{chunk-local state or cumprodsum: }{\mathbf{H}}_{[i]}^r}{\underbrace{\sum _{t=1}^r\left({\beta }_{[i]}^t{\mathbf{v}}_{[i]}^t{\mathbf{k}}_{[i]}^{t\top }\prod _{s=t+1}^r\left(\mathbf{I}-{\beta }_{[i]}^s{\mathbf{k}}_{[i]}^s{\mathbf{k}}_{[i]}^{s\top }\right)\right)}}\\ & ={\mathbf{S}}_{[i]}\left(\mathbf{I}-\sum _{t=1}^r{\mathbf{w}}_{[i]}^t{\mathbf{k}}_{[i]}^{t\top }\right)+\sum _{t=1}^r{\mathbf{u}}_{[i]}^t{\mathbf{k}}_{[i]}^{t\top }\end{array}$$

$w,u$的计算也都从归纳证明中给出

$$\begin{array}{rl}{\mathbf{w}}_{[t]}^r& ={\beta }_{[t]}^r\left({\mathbf{k}}_{[t]}^r-\sum _{i=1}^{r-1}{\mathbf{w}}_{[t]}^i({\mathbf{k}}_{[t]}^i{)}^{\top }{\mathbf{k}}_{[t]}^r\right)\\ {\mathbf{u}}_{[t]}^r& ={\beta }_{[t]}^r\left({\mathbf{v}}_{[t]}^r-\sum _{i=1}^{r-1}{\mathbf{u}}_{[t]}^i({\mathbf{k}}_{[t]}^i{)}^{\top }{\mathbf{k}}_{[t]}^r\right)\end{array}$$

对于输出则有

$$\begin{array}{rl}{\mathbf{o}}_{[i]}^r& ={\mathbf{S}}_{[i]}^r{\mathbf{q}}_{[i]}^r\\ & ={\mathbf{S}}_{[i]}{\mathbf{q}}_{[i]}^r-\sum _{t=1}^r{\mathbf{S}}_{[i]}{\mathbf{w}}_{[i]}^t({\mathbf{k}}_{[i]}^{t\top }{\mathbf{q}}_{[i]}^r)+\sum _{t=1}^r{\mathbf{u}}_{[i]}^t({\mathbf{k}}_{[i]}^{t\top }{\mathbf{q}}_{[i]}^r)\\ & ={\mathbf{S}}_{[i]}{\mathbf{q}}_{[i]}^r+\sum _{t=1}^r({\mathbf{u}}_{[i]}^t-{\mathbf{S}}_{[i]}{\mathbf{w}}_{[i]}^t)({\mathbf{k}}_{[i]}^{t\top }{\mathbf{q}}_{[i]}^r)\end{array}$$

矩阵形式为

$$\begin{array}{rl}{\mathbf{S}}_{[i+1]}& ={\mathbf{S}}_{[i]}(\mathbf{I}-{\mathbf{W}}_{[i]}^{\top }{\mathbf{K}}_{[i]})+{\mathbf{U}}_{[i]}^{\top }{\mathbf{K}}_{[i]}\\ & ={\mathbf{S}}_{[i]}+({\mathbf{U}}_{[i]}-{\mathbf{W}}_{[i]}{\mathbf{S}}_{[i]}^{\top }{)}^{\top }{\mathbf{K}}_{[i]}\in {\mathbb{R}}^{d\times d}\\ {\mathbf{O}}_{[i]}& ={\mathbf{Q}}_{[i]}{\mathbf{S}}_{[i]}^{\top }+({\mathbf{Q}}_{[i]}{\mathbf{K}}_{[i]}^{\top }\odot \mathbf{M})({\mathbf{U}}_{[i]}-{\mathbf{W}}_{[i]}{\mathbf{S}}_{[i]}^{\top })\in {\mathbb{R}}^{C\times d}\end{array}$$

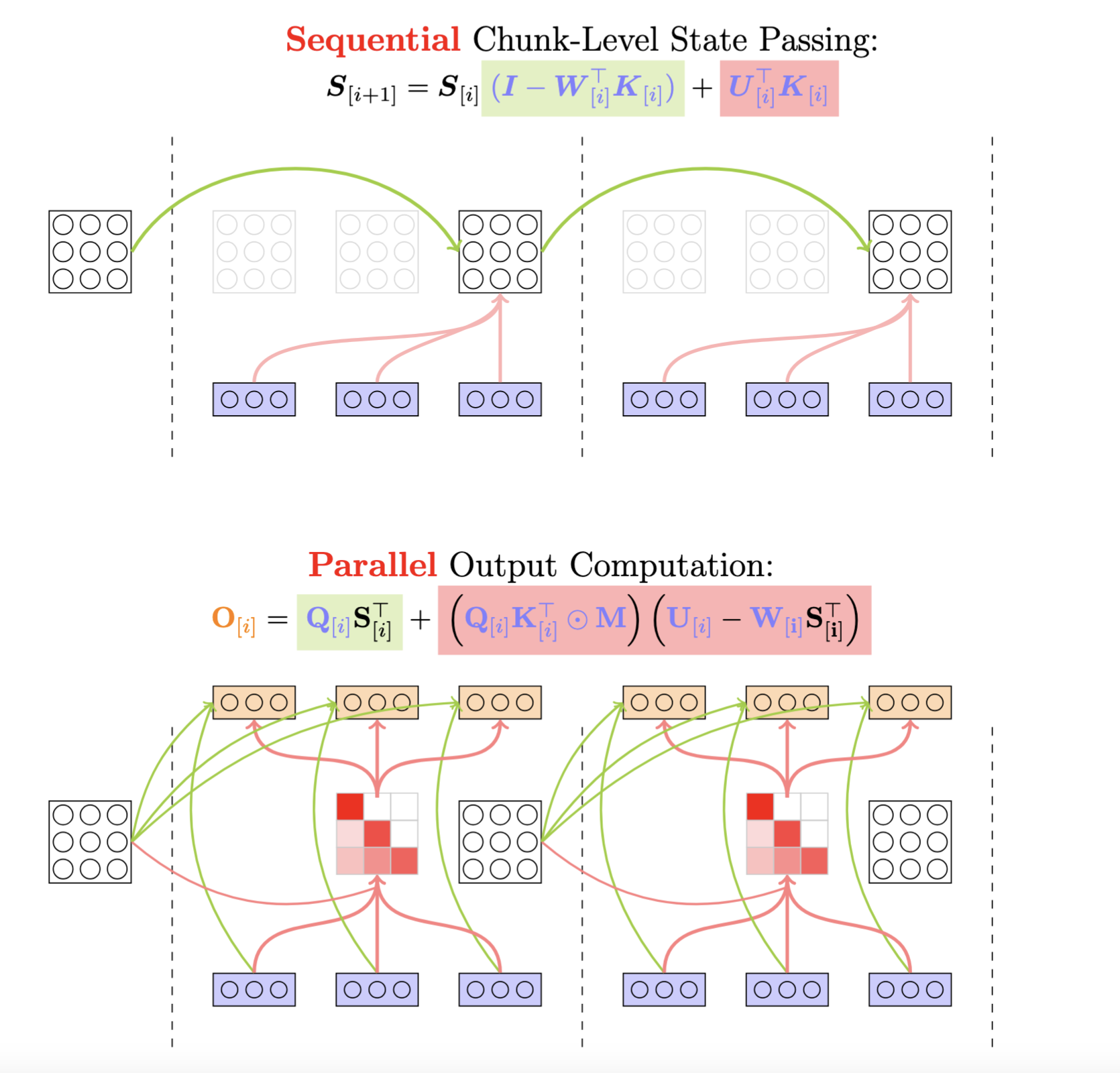
我们进行这些优化的目的是避免状态更新时出现的 无法避免的递归运算，这个运算除了费时之外还需要存储较多的中间结果，如果仔细观察优化后的结果，式子中仍然存在需要递归运算的部分

$$\begin{array}{rl}{\mathbf{w}}_{[t]}^r& ={\beta }_{[t]}^r\left({\mathbf{k}}_{[t]}^r-\sum _{i=1}^{r-1}{\mathbf{w}}_{[t]}^i({\mathbf{k}}_{[t]}^i{)}^{\top }{\mathbf{k}}_{[t]}^r\right)\\ {\mathbf{u}}_{[t]}^r& ={\beta }_{[t]}^r\left({\mathbf{v}}_{[t]}^r-\sum _{i=1}^{r-1}{\mathbf{u}}_{[t]}^i({\mathbf{k}}_{[t]}^i{)}^{\top }{\mathbf{k}}_{[t]}^r\right)\end{array}$$

这会是当前算法计算瓶颈，作者在这里使用了UT transform来进行优化

这里我想找到一个比较符合直觉的解释，如有更好的切入点欢迎修正

可以这么来思考，我们的目的是找到一个矩阵运算(由于$w,u$基本一致，只需要一个形式)，来并行计算出所有块内的$w,u$
但是具体应该怎么找？一般来说会先展开几项看看情况，注意到这里的 $\beta$ 实际上增加了阅读复杂性，完全可以直接设为1或者被对应的$k,v$吸收，所以接下来的过程(除进入结论外)会忽视learning rate
我们以 $w$ 为例

$$\begin{array}{rl}{\mathbf{w}}^1& ={\mathbf{k}}^1\\ {\mathbf{w}}^2& =\left({\mathbf{k}}^2-{\mathbf{w}}^1({\mathbf{k}}^1{)}^{\top }{\mathbf{k}}^2\right)\\ & ={\mathbf{k}}^2-{\mathbf{k}}^1({\mathbf{k}}^1{)}^{\top }{\mathbf{k}}^2\\ {\mathbf{w}}^3& =\left({\mathbf{k}}^3-{\mathbf{w}}^1({\mathbf{k}}^1{)}^{\top }{\mathbf{k}}^3-{\mathbf{w}}^2({\mathbf{k}}^2{)}^{\top }{\mathbf{k}}^3\right)\\ & ={\mathbf{k}}^3-{\mathbf{k}}^1({\mathbf{k}}^1{)}^{\top }{\mathbf{k}}^3+{\mathbf{k}}^1({\mathbf{k}}^1{)}^{\top }{\mathbf{k}}^2({\mathbf{k}}^2{)}^{\top }{\mathbf{k}}^3-{\mathbf{k}}^2({\mathbf{k}}^2{)}^{\top }{\mathbf{k}}^3\end{array}$$

每个式子的形式都是 $k^i-X{k}^i$ ，仔细观察其中的每一项，对于 $w^2$ 来说，是减去一个12的相关项，对于$w^3$来说，是减去一个13相关项，123相关项，23相关项，这可以与某个形式联系起来：以i为起点，i到r的某种影响权重
以 ${\mathbf{k}}^1({\mathbf{k}}^1{)}^{\top }{\mathbf{k}}^2$ 为例，便是以1为起点，从1到2的一个权重 $(k^1{)}^T{k}^2$ ，权重的形式也是统一的，如果中间经过另一个位置，如 ${\mathbf{k}}^1({\mathbf{k}}^1{)}^{\top }{\mathbf{k}}^2({\mathbf{k}}^2{)}^{\top }{\mathbf{k}}^3$，权重为二者相乘，至于出现的负号和加号交替，只要设置权重为负就可以
那什么样的矩阵形式可以得到这样的内容呢？
首先以$i$为起点(经过中间位置)到达指定的点$r$，这可以写成图论问题，将问题抽象成有向无环图，每个点 $i$，如果满足 $i<r$，则存在从$i$指向$r$的路径，这个路径的权重设为 $-(k^i{)}^T{k}^r$，这里省略的$\beta$ 为 ${\beta }^r$ ，于是我们得到邻接矩阵 $A$
为了得到乘积形式的经过中间点的权重，离散数学告诉我们只需要计算$A^n$
至此我们得到了一个严格的下三角阵A，它能与$w,u$的计算联系起来

但是具体应该如何联系？这里有两种切入点，同样直觉性的思考，我们不难从上面的展开式中发现，计算位置3的$w$，我们需要有1到3的权重，1到2到3的权重，2到3的权重，也就是所有到达3的可能路径的权重之和
由于单独的$k^3$存在，结点指向自己的权重可以设置为1
于是$w^3$的计算可以转换成两个矩阵相乘 某个包含所有权重的矩阵$T$与矩阵$K$，有

$$W=TK$$ $$T=I+A+A^2+...$$

这个式子我们已经比较熟悉，它可以写成Householder矩阵$(I-A{)}^{-1}$ ，同时T是一个下三角阵，这样的特性允许我们高效的计算W和U
所以有结论

$${\mathbf{W}}_{[t]}={\mathbf{T}}_{[t]}\mathrm{diag}({\mathbf{\beta }}_{[t]}){\mathbf{K}}_{[t]},{\mathbf{U}}_{[t]}={\mathbf{T}}_{[t]}\mathrm{diag}({\mathbf{\beta }}_{[t]}){\mathbf{V}}_{[t]}$$

实际上直接从数学推到上考虑的话
我们已经得到了矩阵 $A$，根据A的元素，我们可以直接把递归式写成

$$W=K+AW$$

化简得到

$$(I-A)W=K$$ $$W=(I-A{)}^{-1}K$$

同样得到以上结论

Algorithm Performance

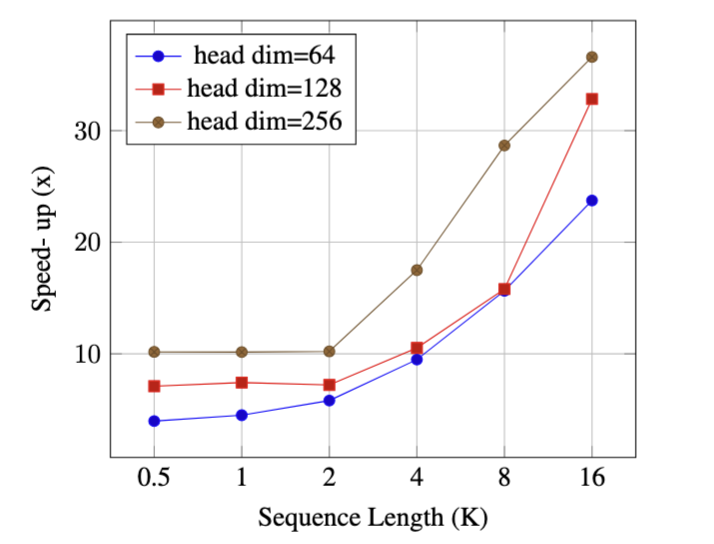
作者实现了recurrent和chunkwise的做法(基于triton)，上图为chunkwise speedup vs. recurrent，可以看到chunkwise快于recurrent同时随着序列增长差异越明显
理论上 chunkwise的FLOPs大于recurrent，作者认为，由于 recurrent 依赖的并行只有 batch 的并行和 head 的并行，无法高效使用现代GPU的并行硬件，随着序列增长，无法在序列维度上并行的recurrent与chunkwise速度差异越来越大(而chunkwise相反，尽管计算量大但是高度并行能够高效利用GPU)

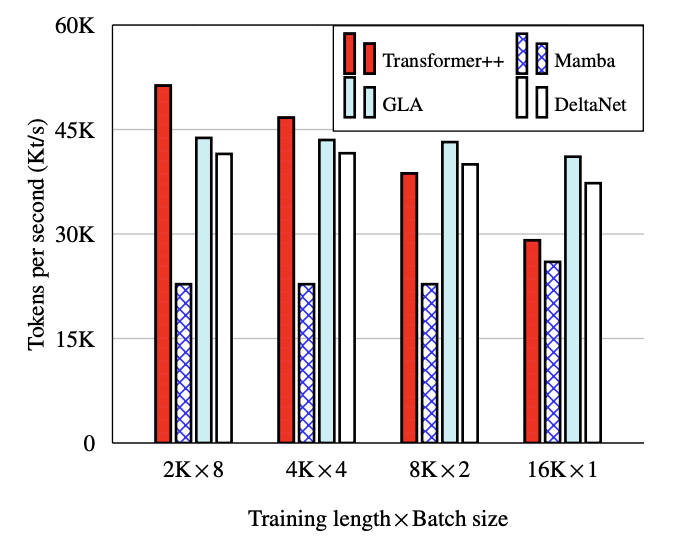
与其它架构相比，DeltaNet的算法低于GLA和Transformer，但差距不是很大

The Architecture

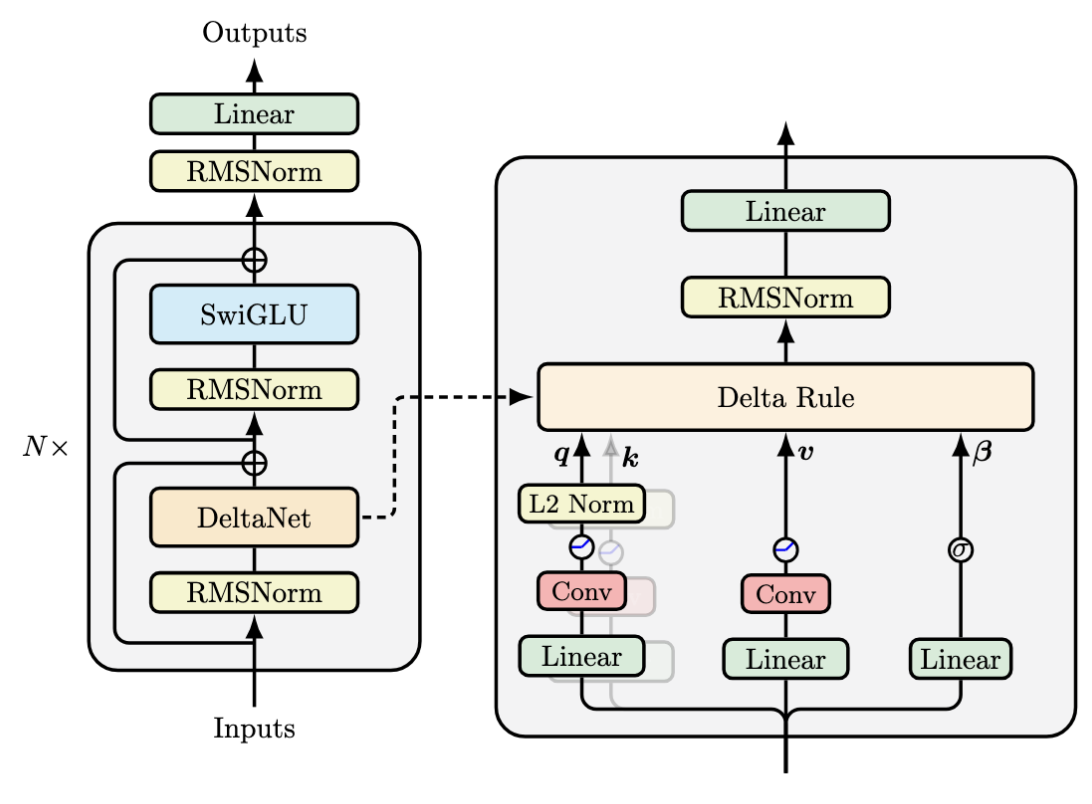
与transformer-based的主要区别是 token mixing (self-attention - DeltaNet) 和 channel mixing (FFN - SwiGLU)，主要的创新点在于 short conv，L2 norm + SiLU activation(相比于其它工作的L1 norm, 1+ELU)

到记录这篇笔记的时候，有一些transformer-based前沿模型已经对q,k进行了normalization，例如Qwen3等使用RMSnorm或其变体，这里的L2 norm在苏神的博客也有提到，在transformer-based中有利于外推

为什么要对Queries和Key进行归一化？
除了作为trick之外，对k的归一化对数值稳定性十分重要
DeltaNet 的核心状态更新为

$${\mathbf{S}}_t={\mathbf{S}}_{t-1}(\mathbf{I}-{\beta }_t{\mathbf{k}}_t{\mathbf{k}}_t^{\top })+{\mathbf{v}}_t{\mathbf{k}}_t^{\top }$$

$S$的数值稳定性取决于 transition matrix $I=\beta k{k}^T$的特征值，我们希望所有的特征值(的范数)$\le 1$
在与k正交的方向上，矩阵的特征值为1，在k方向上，特征值为$1-{\beta }_t\Vert {\mathbf{k}}_t{\Vert }^2$，所以我们需要对k进行归一化。这里归一化的方法有很多，如果选择 L2 normalization，当$\beta =1,||k|{|}^2=1$的时候，我们会把原状态$S_{t-1}$中k方向的分量删除，让状态更新更加干净(L2 normalization天然适合Delta Rule)
而对Q的归一化，主要是性能表现的提升，在近期的QK-normalization研究中有相关的讨论

另外的是，由于特殊的矩阵性质和L2 normalization，transition matrix的特征值都 $>0$（注意$\beta$经过的激活函数是sigmoid），在相关研究中这样的做法限制了状态的跟踪能力，可以通过令 $\beta =2\beta$来尝试解决

关于output的归一化
之前的linear attention会在注意力计算结束之后会对attention weight进行归一化

$${\mathbf{o}}_t=\frac{\left({\sum }_{i=1}^t{\mathbf{v}}_i\varphi (\mathbf{k}{)}_i^{\top }\right)\varphi (\mathbf{q}{)}_t}{{\sum }_{i=1}^t\varphi (\mathbf{k}{)}_i^{\top }\varphi (\mathbf{q}{)}_t}$$

有工作指出，这样的做法可能出现unbounded gradients和不稳定的情况，更好的做法是去除分母，然后额外进行归一化，最后再做projection

Short Convolution & Induction head

DeltaNet中使用了short conv

short conv个人认为是一个比较值得一提的做法，因此单独开一个小章节
我希望大概了解，什么是shotr conv，什么是induction head，和它们之间的联系，下文也会按照这样的顺序进行记录

Short Conv

short convolution是指 kernel size比较小，注重局部信息的卷积，一般使用depthwise separable 1D卷积层，每个channel先分开处理之后再通过1x1卷积核聚合，参数量计算量比较少。在Linear attention的很多模型中都会使用
DeltaNet中使用的short convolution，kernel size是4，对qkv都进行了卷积

这里主要是想通过short conv的数学形式来看看它的作用，假若kernel size为2，short conv做的其实是，对任意输入$x$

$$x_t^{\prime }=w[0,d]x_{t-1}[d]+w[1,d]x_t[d]$$

也就是相邻两个token的q/k/v的某种加权和，这个加权和是channel维度的，两个相邻时间的每个channel自由选择保留的程度进行weighted sum，得到新的$x_t$
这样做的作用，一个比较受认可的解释是Anthropic提出的induction head，用于上下文能力的提升
同时，值得一提的是RWKV的做法是线性插值，称token shift

$$u_r\odot x_{t-1}+(1-u_r)\odot x_t$$

这里的$\odot$是element-wise的，同样是每个维度进行不同的加权，只不过这里限制了权重和为1

这就不得不提到Linear Attention领域当前的争论/骂战，RWKV作者在2020年使用了token shift，为了增强上下文强度，Anthropic两篇相关论文《A Mathematical Framework for Transformer Circuits》《In context learning and Induction head》分别是2021，2022；尽管RWKV没有给出详细的理论说明(两份工作完全是不同性质的)，确实Anthropic提到的induction head与token shift是高度相关的 后续DeltaNet等其它模型进行short conv的时候争议就出现了

Induction Head

Anthropic在2021年的工作A Mathematical Framework for Transformer Circuits和 2022年的工作In-context Learning and Induction Heads发现并论证(不见得十分充分)了transformer 存在 Induction Head的机制，同时该机制与ICL高度相关

这两份解释性的工作个人认为是比较有意思的，贡献很大

我们分别进行记录

A Mathematical Framework for Transformer Circuits 主要是通过电路的角度尝试分析transformer的内部机制(只考虑纯attention无MLP的transformer，因为MLP不好进行电路分析)，核心贡献在于提出了两个电路(QK电路和OV电路)和三种组合(Q-Composition, K-Composition, V-Composition)，其中两个电路与K-Composition初步指出了Induction Head的存在
论文发现：模型通过QK电路决定注意力分配，通过OV电路进行结果聚合。两层注意力形成了固定的任务分配，由第一层进行“shift”，第二层进行“match”
当处理第$t$个token时，第一层QK电路会为$t-1$分配高注意力，OV电路将$t-1$个token的信息输入了残差流的子空间，此时进入下一层的$x_t$主要包含当前token的信息+前一个token的信息(和其它token的组合信息，极少数)。对于第二层，权重矩阵$W_Q$会重点提取出$x_t$中属于$t$时刻的信息(Q-Composition没有发生或强度低)，而$W_K$则基本提取了来自前一个token的信息(K-Composition)，此时的注意力计算$q_t{k}_j$，实际上变成了$q_t{k}_{j-1}$，即识别当前token与历史token的前一个token的相似程度(QK电路)。很自然地，如果相似，分配高注意力分数。此时该层的OV电路倾向于“复制”匹配到的token的$v_j$，并为分类得到该token增强对应的logit

从数学形式来看是这样的
从Layer 0 输入到 Layer 1的残差流

$${\mathbf{x}}_t^{(1)}={\mathbf{x}}_t^{(\text{embed})}+{\mathbf{W}}_{\text{OV}}^{{\mathbf{h}}_0}\cdot {\mathbf{x}}_{t-1}$$

Layer 1发生K-Composition

$$\begin{array}{rl}{\mathbf{k}}_t& ={\mathbf{W}}_{\mathbf{K}}^{{\mathbf{h}}_1}\cdot \left[{\mathbf{x}}_t^{(\text{embed})}+{\mathbf{W}}_{\text{OV}}^{{\mathbf{h}}_0}\cdot {\mathbf{x}}_{t-1}\right]\\ & =\underset{\text{当前token信息}}{\underbrace{{\mathbf{W}}_{\mathbf{K}}^{{\mathbf{h}}_1}\cdot {\mathbf{x}}_t^{(\text{embed})}}}+\underset{\text{位移后的前序token信息}}{\underbrace{{\mathbf{W}}_{\mathbf{K}}^{{\mathbf{h}}_1}\cdot {\mathbf{W}}_{\text{OV}}^{{\mathbf{h}}_0}\cdot {\mathbf{x}}_{t-1}}}\end{array}$$

使用 $f$ 代表Q-transform，$g$代表K-transform的话，发生K-Composition(强度大)时，注意力计算变成

$$\mathbf{score}(\mathbf{t},\mathbf{j})\propto \mathbf{exp}(\mathbf{f}({\mathbf{x}}_t)\cdot \mathbf{g}({\mathbf{x}}_{j-1}))$$

虽然这里是 $j-1$，但实际上位置对应的是 $j$，如果存在高相似度，注意力分数高，自然会将$v_j$ 复制过来
后续便是output logit的运算，分类得到j位置的token

Induction Head指的就是K-Composition的过程，也就是说，在简单的结构时(两层attention-only的transformer)，NTP的预测更多依赖于n-gram或者说最近邻匹配，直接复制历史出现过的token的下一个，很符合直觉

而In-context Learning and Induction Heads进行了更大规模的实验，通过对Induction Head的消融与ICL能力的评估，论文较完整地证明了Induction Head与ICL高度相关。在更复杂的模型中，NTP一开始会依赖于n-gram，但在达到其预测的某一极限后，模型会突然学会反事实(与历史不同的预测)的预测，可能的解释是Induction Head学会了更高层次的匹配，能够理解高维语义信息(用语义完成Induction过程)而不只是相同token的复制

二者的关系

至此要理解 short conv 和 induction head就很简单了，直接实现induction head的方法就是建立相邻两个token之间的联系，让Key能够选择对相邻token信息的去留(实现K-Composition)。无论是short conv还是token shift都直接实现了这一点(而不像transformer一样需要两层来实现)，至于要不要实现QV的short conv，应该暂无定论

transformer通过两层实现Induction Head可以看成是一种冗余，可能为transformer增加short conv或token shift也会是Linear Attention的可能反哺

另外的，shortconv是更为接受的方式，除了争论之外，一种可能的原因是相比起token shift的线性插值，shortconv的灵活性更强(例如不限制和为1，参数量更多等)，kernel size有限的情况(认为2就足够)下，选择 short conv不会增加太多参数，可能使其成为了比较好的解法

Hybrid Models

作者进行了混合注意力的尝试
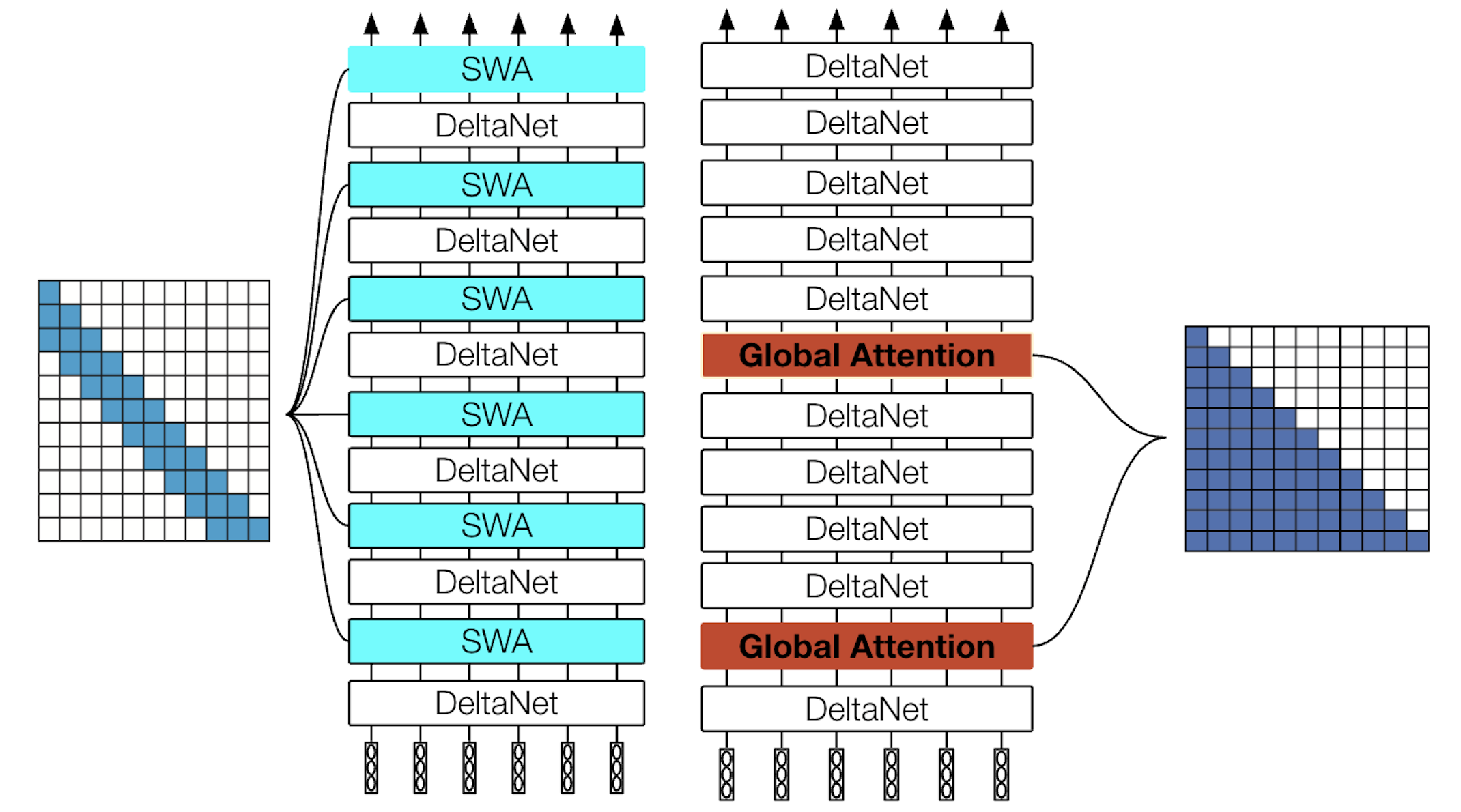第一种是SWA+DeltaNet，尽管计算复杂度低于平方，从设计上来看会(与RNN同样)面临retrival的问题；第二种是Full Attention + DeltaNet，计算复杂度为平方，尽管只设置了两层Full Attention

在340M的参数量下，模型表现为

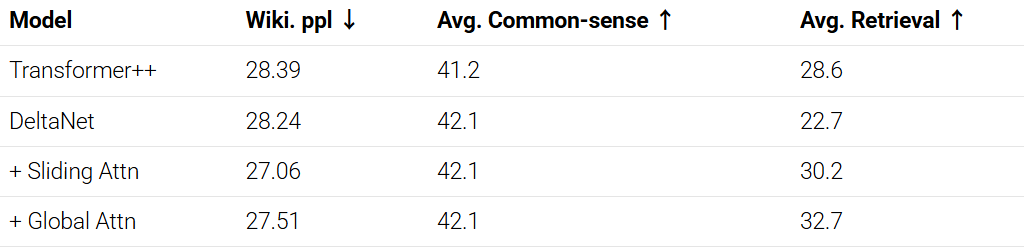
彼此都是comparable，差距不是很明显

在1.3B的参数量下，第一种方案在retrival上的缺陷就暴露出来

也就证明，在scale up之后，SWA+DeltaNet的Retrival能力跟不上Full Attention
这可能对后续的混合注意力设计有所帮助

Gated DeltaNet

在简史中我们已经知道Gated DeltaNet的核心改进在于引入decay

$${\mathbf{S}}_t={\mathbf{S}}_{t-1}\left({\mathbf{\alpha }}_t(\mathbf{I}-{\mathbf{\beta }}_t{\mathbf{k}}_t{\mathbf{k}}_t^{\mathbf{T}})\right)+{\mathbf{\beta }}_t{\mathbf{v}}_t{\mathbf{k}}_t^{\mathbf{T}}$$

对于模型设计方面应该没有太多值得讨论的，所以对于模型设计这个章节将集中在代表性工作Qwen-NexT和Kimi Linear上，尝试深入看看代码实现，然后可能最后看看它们的训练过程

Qwen-Next

Qwen-Next 是混合架构，是Gated DeltaNet + Gated Attention(Full Attention) + MoE组成。
48个transformer block，Linear Attention与Full Attention的比例是3:1，而对于MoE则是512个Expert，每个token激活11个Expert(10个routed，1个shared)，80B参数量激活3B参数(3.75%)

整个模型架构为

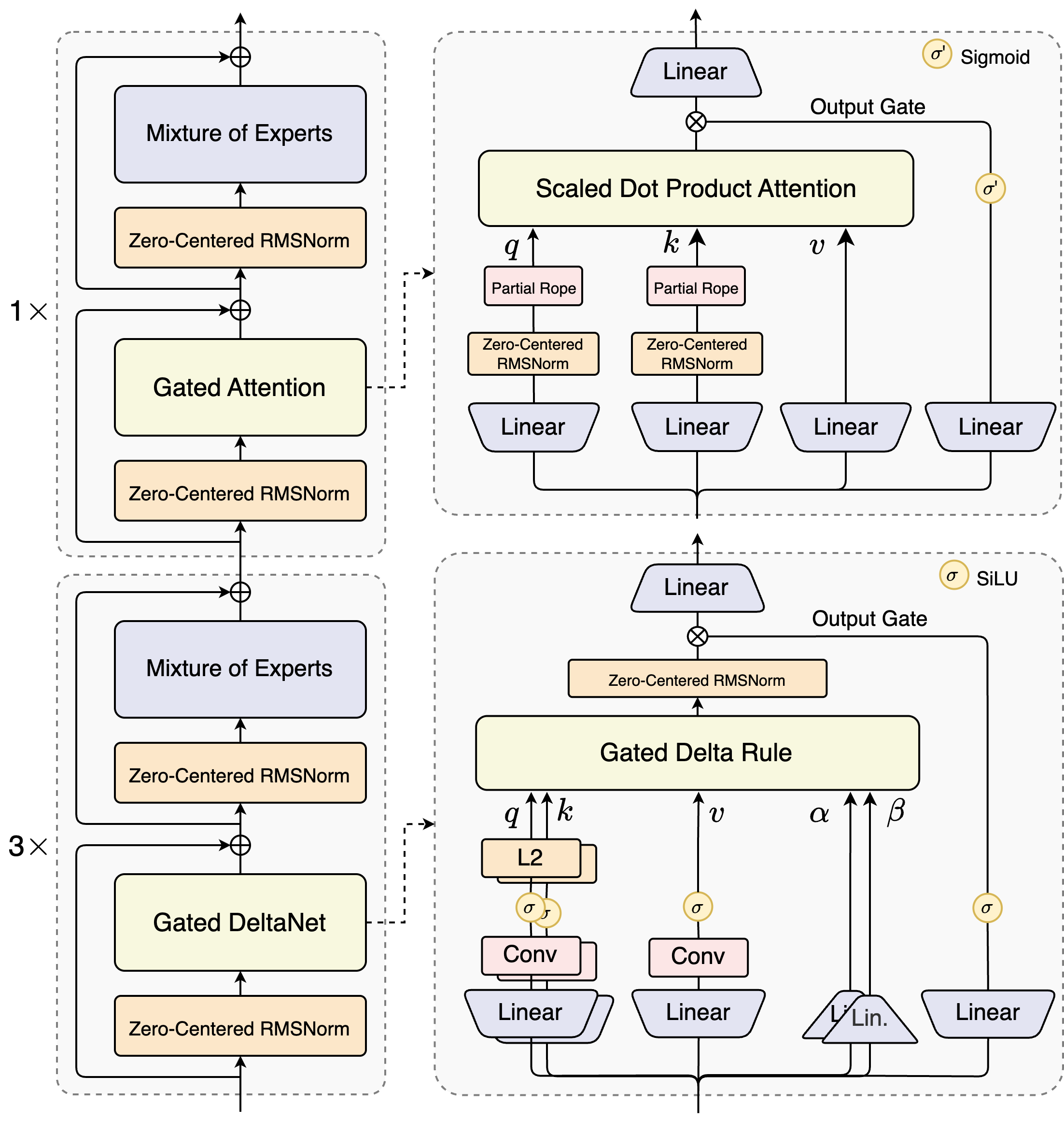
根据官方的technical blog中的描述，核心设计主要包含以下几个方面

• Gated Attention + head dim增加(128-256) + 仅对前25%进行RoPE(外推)
  • 来自Qwen团队工作 [2505.06708] Gated Attention for Large Language Models: Non-linearity, Sparsity, and Attention-Sink-Free
• 更加稀疏的MoE
  • 80B，仅激活3B，扩展到512个专家
• QK-Norm
  • 使用 Zero-Centered RMSNorm，对norm weight施加decay，旨在避免norm weight的异常数值
• Multi-Token Prediction(MTP)

模型的主要优势是训练成本低(计算量少)，推理速度快(吞吐大)，表现超过Qwen自家同时期的dense和激活参数量相同的MoE，但是个人感觉Thinking模式没train好或者不适合thinking，表现略差

接下来重点看看 Gated Attention + Gated DeltaNet + QK-Norm + MTP(补一下MTP知识)

Gated Attention

Claim: Gated Attention有利于training stability，消除 attention sink 和 massive activations
Qwen-Next中的实现是这样的(来自transformers/src/transformers/models/qwen3_next/modular_qwen3_next.py at main · huggingface/transformers · GitHub)
先在Attention中为Gate分配参数

self.q_proj = nn.Linear(
	config.hidden_size, config.num_attention_heads * self.head_dim * 2, bias=config.attention_bias
)

forward 里进行对应的操作

input_shape = hidden_states.shape[:-1] # B, N
query_states, gate = torch.chunk(
	self.q_proj(hidden_states).view(*input_shape, -1, self.head_dim * 2), 2, dim=-1
) # B, N, H, Hdim
gate = gate.reshape(*input_shape, -1) # B, N, C
 
# attention计算得到结果，在投影之前....
 
attn_output = attn_output.reshape(*input_shape, -1).contiguous()
        attn_output = attn_output * torch.sigmoid(gate)

可以看到是在最后的时候，对每个token进行Gate，决定每个token的每个channel的留取量

这里顺便提一下之前有疑惑的对attention weight进行dropout
attention weight的dropout发生在Value加权之前，目的是避免模型过度学习token的对应关系，通过随机丢弃attention weight来避免过拟合，即使丢弃的token对next token prediction很重要
而Gated则是希望模型学会捕捉哪些token更加重要，选择性的筛选对应的信息量

这个方法的原论文获得了Nips best paper award，值得一读

Qwen3-Next Gated DeltaNet

看看GatedDetlaNet大概是怎么写的

class Qwen3NextGatedDeltaNet(nn.Module):
    def __init__(self, config: Qwen3NextConfig, layer_idx: int):
		super().__init__()
        # dim & size initialization
        # ...
        self.layer_idx = layer_idx # 通过layer idx来管理参数和每一层的计算似乎越来越流行？
        # ...
        self.conv_dim = self.key_dim * 2 + self.value_dim # Q dim + K dim + Value dim
        self.conv1d = nn.Conv1d(
            in_channels=self.conv_dim,
            out_channels=self.conv_dim,
            bias=False,
            kernel_size=self.conv_kernel_size,
            groups=self.conv_dim, # Depth-wise convolution
            padding=self.conv_kernel_size - 1,
        )
 
        # projection of the input hidden states
        projection_size_qkvz = self.key_dim * 2 + self.value_dim * 2
        projection_size_ba = self.num_v_heads * 2
        
 
        # time step projection (discretization)
        # instantiate once and copy inv_dt in init_weights of PretrainedModel
        self.dt_bias = nn.Parameter(torch.ones(self.num_v_heads))
        A = torch.empty(self.num_v_heads).uniform_(0, 16)
        self.A_log = nn.Parameter(torch.log(A))
 
        self.norm = (
            Qwen3NextRMSNormGated(self.head_v_dim, eps=self.layer_norm_epsilon)
            if FusedRMSNormGated is None
            else FusedRMSNormGated(
                self.head_v_dim,
                eps=self.layer_norm_epsilon,
                activation=self.activation,
                device=torch.cuda.current_device(),
                dtype=config.dtype if config.dtype is not None else torch.get_default_dtype(),
            )
        )
 
        self.causal_conv1d_fn = causal_conv1d_fn
        self.causal_conv1d_update = causal_conv1d_update or torch_causal_conv1d_update
        self.chunk_gated_delta_rule = chunk_gated_delta_rule or torch_chunk_gated_delta_rule
        self.recurrent_gated_delta_rule = fused_recurrent_gated_delta_rule or torch_recurrent_gated_delta_rule

一些除注释外较长的补充说明

• qkvz 中的z用于实现GatedRMSNorm，用于计算 F.silu(z.to(torch.float32))，也就是Gated
• dt_bias和A_log 用于计算GatedDeltaNet的gate decay，来自 Mamba，实现data-dependant的state decay
  • g = -self.A_log.float().exp() * F.softplus(a.float() + self.dt_bias)
• 按照官方博客给出的架构图，在DeltaNet block内部使用的normalization方法是Gated版本的zero-centered RMSNorm，但是代码中实际上是 RMSNormGated
• casual_conv1d_fn 用于训练，此时并行输入，可以直接做卷积；causal_conv1d_update 用于推理，由于自回归，需要存储 conv_state，也就缓存前3个token的状态来计算卷积

def forward(
	self,
	hidden_states: torch.Tensor,
	cache_params: Optional[Qwen3NextDynamicCache] = None,
	cache_position: Optional[torch.LongTensor] = None,
	attention_mask: Optional[torch.Tensor] = None,
):
	# qkvz, ab porjection and convolution and conv state update
 
	if not use_precomputed_states:
		core_attn_out, last_recurrent_state = self.chunk_gated_delta_rule(
			query,
			key,
			value,
			g=g,
			beta=beta,
			initial_state=None,
			output_final_state=cache_params is not None,
			use_qk_l2norm_in_kernel=True,
		)
 
	else:
		core_attn_out, last_recurrent_state = self.recurrent_gated_delta_rule(
			query,
			key,
			value,
			g=g,
			beta=beta,
			initial_state=recurrent_state,
			output_final_state=cache_params is not None,
			use_qk_l2norm_in_kernel=True,
		)
 
	# Update cache
	if cache_params is not None:
		cache_params.recurrent_states[self.layer_idx] = last_recurrent_state
 
	z_shape_og = z.shape
	# reshape input data into 2D tensor
	core_attn_out = core_attn_out.reshape(-1, core_attn_out.shape[-1])
	z = z.reshape(-1, z.shape[-1])
	core_attn_out = self.norm(core_attn_out, z)
	core_attn_out = core_attn_out.reshape(z_shape_og)
	core_attn_out = core_attn_out.reshape(core_attn_out.shape[0], core_attn_out.shape[1], -1)
 
	output = self.out_proj(core_attn_out)
	return output

重点看看delta rule如何计算
推理的时候使用recurrent实现，训练的时候使用chunk实现，两种计算 Flash Linear Attention都实现了高效的版本 chunk_gated_delta_rule, fused_recurrent_gated_delta_rule
同时代码中分别提供了一个pytorch的平替版

对于recurrent

def torch_recurrent_gated_delta_rule(
    query, key, value, g, beta, initial_state, output_final_state, use_qk_l2norm_in_kernel=False
):
    batch_size, num_heads, sequence_length, k_head_dim = key.shape
    v_head_dim = value.shape[-1]
    scale = 1 / (query.shape[-1] ** 0.5) # 甚至有scale
    query = query * scale
 
    core_attn_out = torch.zeros(batch_size, num_heads, sequence_length, v_head_dim).to(value)
    last_recurrent_state = (
        torch.zeros(batch_size, num_heads, k_head_dim, v_head_dim).to(value)
        if initial_state is None
        else initial_state.to(value)
    )
 
    for i in range(sequence_length):
        q_t = query[:, :, i]
        k_t = key[:, :, i]
        v_t = value[:, :, i]
        g_t = g[:, :, i].exp().unsqueeze(-1).unsqueeze(-1)
        beta_t = beta[:, :, i].unsqueeze(-1)
 
        last_recurrent_state = last_recurrent_state * g_t
        kv_mem = (last_recurrent_state * k_t.unsqueeze(-1)).sum(dim=-2)
        delta = (v_t - kv_mem) * beta_t
        last_recurrent_state = last_recurrent_state + k_t.unsqueeze(-1) * delta.unsqueeze(-2)
        core_attn_out[:, :, i] = (last_recurrent_state * q_t.unsqueeze(-1)).sum(dim=-2)
 
    if not output_final_state:
        last_recurrent_state = None
    core_attn_out = core_attn_out.transpose(1, 2).contiguous().to(initial_dtype)
    return core_attn_out, last_recurrent_state

核心逻辑

last_recurrent_state = (
	torch.zeros(batch_size, num_heads, k_head_dim, v_head_dim).to(value)
	if initial_state is None
	else initial_state.to(value)
)
 
for i in range(sequence_length):
	q_t = query[:, :, i]
	k_t = key[:, :, i]
	v_t = value[:, :, i]
	g_t = g[:, :, i].exp().unsqueeze(-1).unsqueeze(-1)
	beta_t = beta[:, :, i].unsqueeze(-1)
 
	last_recurrent_state = last_recurrent_state * g_t
	kv_mem = (last_recurrent_state * k_t.unsqueeze(-1)).sum(dim=-2)
	delta = (v_t - kv_mem) * beta_t
	last_recurrent_state = last_recurrent_state + k_t.unsqueeze(-1) * delta.unsqueeze(-2)
	core_attn_out[:, :, i] = (last_recurrent_state * q_t.unsqueeze(-1)).sum(dim=-2)
	core_attn_out = core_attn_out.transpose(1, 2).contiguous().to(initial_dtype)

回忆GatedDeltaNet的公式为

$${\mathbf{S}}_t={\mathbf{S}}_{t-1}\left({\mathbf{\alpha }}_t(\mathbf{I}-{\mathbf{\beta }}_t{\mathbf{k}}_t{\mathbf{k}}_t^{\mathbf{T}})\right)+{\mathbf{\beta }}_t{\mathbf{v}}_t{\mathbf{k}}_t^{\mathbf{T}}$$

这里实现的逻辑应该是遵循了DeltaNet原本的顺序，希望把delta单独拿出来计算

$$\begin{array}{rl}{\mathbf{S}}_t& ={\mathbf{\alpha }}_t{\mathbf{S}}_{t-1}-({\mathbf{\alpha }}_t{\mathbf{S}}_{t-1}{\mathbf{k}}_t-{\mathbf{v}}_t){\mathbf{\beta }}_t{\mathbf{k}}_t^{\mathbf{T}}\\ & ={\mathbf{\alpha }}_t{\mathbf{S}}_{t-1}+({\mathbf{v}}_t-{\mathbf{\alpha }}_t{\mathbf{S}}_{t-1}{\mathbf{k}}_t){\mathbf{\beta }}_t{\mathbf{k}}_t^{\mathbf{T}}\end{array}$$

先计算衰减后的last_recurrent_state，计算括号内的delta，将两者相加更新last_recurrent_state，然后再用query计算attention out
Recurrent的逻辑很简单，就是直接实现公式的写法

对于chunkwise

def torch_chunk_gated_delta_rule(
    query,
    key,
    value,
    g,
    beta,
    chunk_size=64,
    initial_state=None,
    output_final_state=False,
    use_qk_l2norm_in_kernel=False,
):
    # transpose & padding ...
 
    v_beta = value * beta.unsqueeze(-1)
    k_beta = key * beta.unsqueeze(-1)
    # reshape to chunks
    query, key, value, k_beta, v_beta = [
        x.reshape(x.shape[0], x.shape[1], -1, chunk_size, x.shape[-1]) for x in (query, key, value, k_beta, v_beta)
    ]
    g = g.reshape(g.shape[0], g.shape[1], -1, chunk_size)
    mask = torch.triu(torch.ones(chunk_size, chunk_size, dtype=torch.bool, device=query.device), diagonal=0)
 
    # chunk decay
    g = g.cumsum(dim=-1)
    decay_mask = ((g.unsqueeze(-1) - g.unsqueeze(-2)).tril().exp().float()).tril()
    attn = -((k_beta @ key.transpose(-1, -2)) * decay_mask).masked_fill(mask, 0)
    for i in range(1, chunk_size):
        row = attn[..., i, :i].clone()
        sub = attn[..., :i, :i].clone()
        attn[..., i, :i] = row + (row.unsqueeze(-1) * sub).sum(-2)
    attn = attn + torch.eye(chunk_size, dtype=attn.dtype, device=attn.device)
    value = attn @ v_beta
    k_cumdecay = attn @ (k_beta * g.exp().unsqueeze(-1))
    # for each chunk
    for i in range(0, total_sequence_length // chunk_size):
        q_i, k_i, v_i = query[:, :, i], key[:, :, i], value[:, :, i]
        attn = (q_i @ k_i.transpose(-1, -2) * decay_mask[:, :, i]).masked_fill_(mask, 0)
        v_prime = (k_cumdecay[:, :, i]) @ last_recurrent_state
        v_new = v_i - v_prime
        attn_inter = (q_i * g[:, :, i, :, None].exp()) @ last_recurrent_state
        core_attn_out[:, :, i] = attn_inter + attn @ v_new
        last_recurrent_state = (
            last_recurrent_state * g[:, :, i, -1, None, None].exp()
            + (k_i * (g[:, :, i, -1, None] - g[:, :, i]).exp()[..., None]).transpose(-1, -2) @ v_new
        )
 
    if not output_final_state:
        last_recurrent_state = None
    core_attn_out = core_attn_out.reshape(core_attn_out.shape[0], core_attn_out.shape[1], -1, core_attn_out.shape[-1])
    core_attn_out = core_attn_out[:, :, :sequence_length]
    core_attn_out = core_attn_out.transpose(1, 2).contiguous().to(initial_dtype)
    return core_attn_out, last_recurrent_state

chunkwise的计算遵循的同样是

$${\mathbf{W}}_{[t]}={\mathbf{T}}_{[t]}\mathrm{diag}({\mathbf{\beta }}_{[t]}){\mathbf{K}}_{[t]},{\mathbf{U}}_{[t]}={\mathbf{T}}_{[t]}\mathrm{diag}({\mathbf{\beta }}_{[t]}){\mathbf{V}}_{[t]}$$ $$\begin{array}{rl}{\mathbf{S}}_{[i+1]}& ={\mathbf{S}}_{[i]}(\mathbf{I}-{\mathbf{W}}_{[i]}^{\top }{\mathbf{K}}_{[i]})+{\mathbf{U}}_{[i]}^{\top }{\mathbf{K}}_{[i]}\\ & ={\mathbf{S}}_{[i]}+({\mathbf{U}}_{[i]}-{\mathbf{W}}_{[i]}{\mathbf{S}}_{[i]}^{\top }{)}^{\top }{\mathbf{K}}_{[i]}\in {\mathbb{R}}^{d\times d}\\ {\mathbf{O}}_{[i]}& ={\mathbf{Q}}_{[i]}{\mathbf{S}}_{[i]}^{\top }+({\mathbf{Q}}_{[i]}{\mathbf{K}}_{[i]}^{\top }\odot \mathbf{M})({\mathbf{U}}_{[i]}-{\mathbf{W}}_{[i]}{\mathbf{S}}_{[i]}^{\top })\in {\mathbb{R}}^{C\times d}\end{array}$$

只不过增加了Gate

分成两个部分，我们先计算 W 和 U

g = g.cumsum(dim=-1)
decay_mask = ((g.unsqueeze(-1) - g.unsqueeze(-2)).tril().exp().float()).tril()
attn = -((k_beta @ key.transpose(-1, -2)) * decay_mask).masked_fill(mask, 0)
for i in range(1, chunk_size):
	row = attn[..., i, :i].clone()
	sub = attn[..., :i, :i].clone()
	attn[..., i, :i] = row + (row.unsqueeze(-1) * sub).sum(-2)
attn = attn + torch.eye(chunk_size, dtype=attn.dtype, device=attn.device)
value = attn @ v_beta
k_cumdecay = attn @ (k_beta * g.exp().unsqueeze(-1))

这里的attn实际上是之前谈到的邻接矩阵 A，遍历chunk_size和加一个单位阵计算矩阵T，然后根据T计算得到 W(k_cumdecay)，U(value)

再然后正式计算注意力

for i in range(0, total_sequence_length // chunk_size):
	q_i, k_i, v_i = query[:, :, i], key[:, :, i], value[:, :, i]
	attn = (q_i @ k_i.transpose(-1, -2) * decay_mask[:, :, i]).masked_fill_(mask, 0)
	v_prime = (k_cumdecay[:, :, i]) @ last_recurrent_state
	v_new = v_i - v_prime
	attn_inter = (q_i * g[:, :, i, :, None].exp()) @ last_recurrent_state
	core_attn_out[:, :, i] = attn_inter + attn @ v_new
	last_recurrent_state = (
		last_recurrent_state * g[:, :, i, -1, None, None].exp()
		+ (k_i * (g[:, :, i, -1, None] - g[:, :, i]).exp()[..., None]).transpose(-1, -2) @ v_new
	)

$${\mathbf{O}}_{[i]}={\mathbf{Q}}_{[i]}{\mathbf{S}}_{[i]}^{\top }+({\mathbf{Q}}_{[i]}{\mathbf{K}}_{[i]}^{\top }\odot \mathbf{M})({\mathbf{U}}_{[i]}-{\mathbf{W}}_{[i]}{\mathbf{S}}_{[i]}^{\top })\in {\mathbb{R}}^{C\times d}$$

先计算中间的标准attn $({\mathbf{Q}}_{[i]}{\mathbf{K}}_{[i]}^{\top }\odot \mathbf{M})$ attn，再计算与其相乘的 $({\mathbf{U}}_{[i]}-{\mathbf{W}}_{[i]}{\mathbf{S}}_{[i]}^{\top })$ v_new，计算第一项 ${\mathbf{Q}}_{[i]}{\mathbf{S}}_{[i]}^{\top }$ attn_inter，最后进行相加得到attn_out

至于状态更新

$${\mathbf{S}}_{[i+1]}={\mathbf{S}}_{[i]}+({\mathbf{U}}_{[i]}-{\mathbf{W}}_{[i]}{\mathbf{S}}_{[i]}^{\top }{)}^{\top }{\mathbf{K}}_{[i]}\in {\mathbb{R}}^{d\times d}$$

中间项就是 v_new，与K相乘后加入旧状态，得到新的 last_recurrent_state

至于flash linear attention内部是怎么实现的，fla是基于triton实现的，等我学习triton之后可能再回来看看

QK-Norm

MTP

RWKV

RWKV 专题