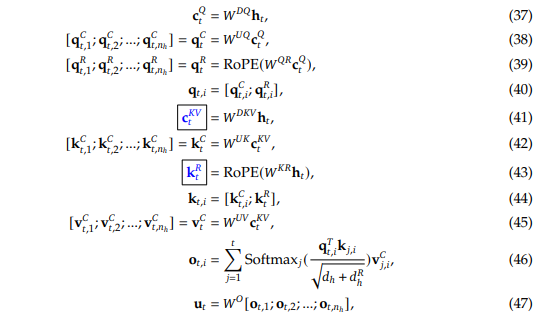KV cache

Overview

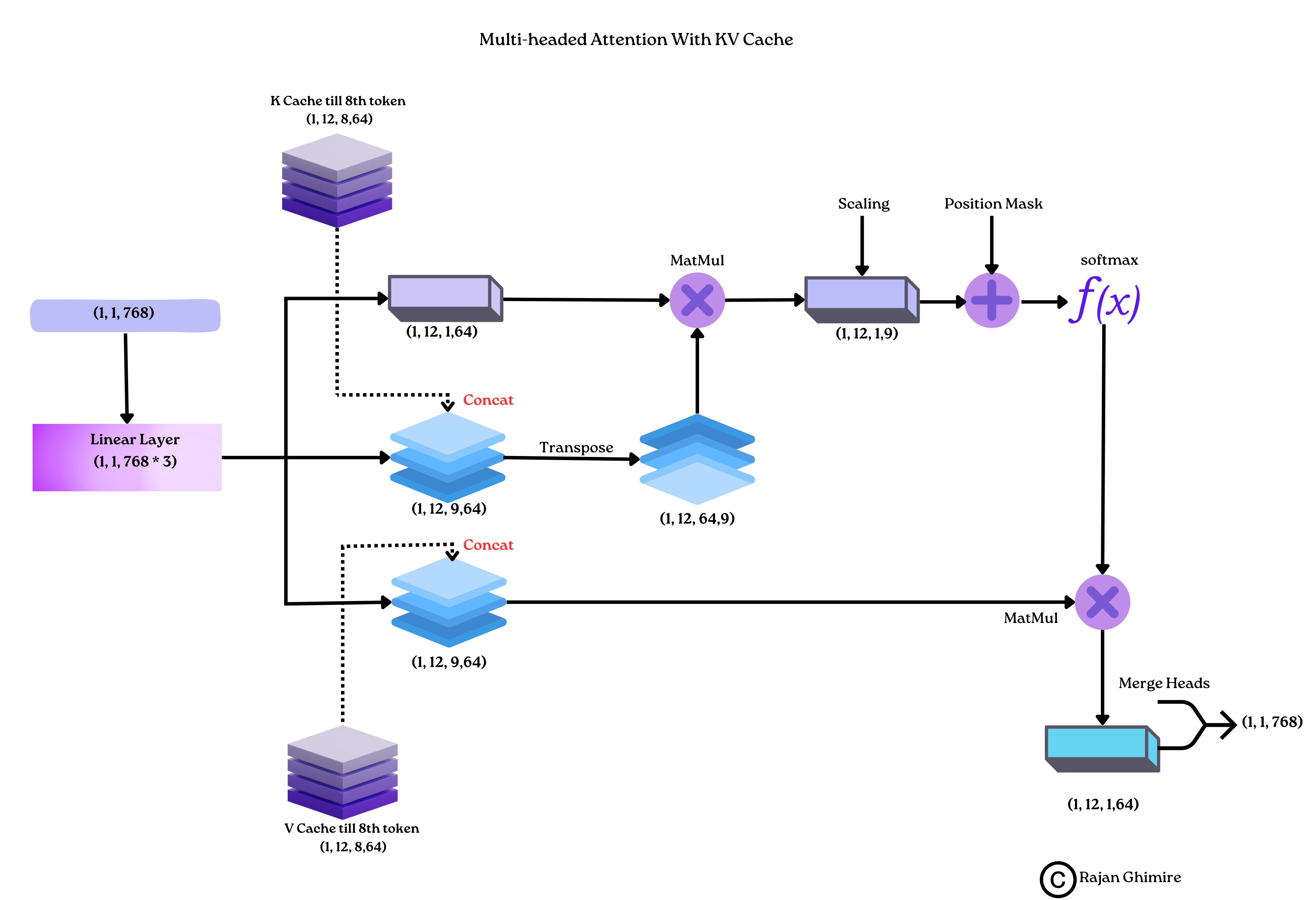
KV cache是缓存注意力机制运算中 key 和 value 的技术
在自回归生成任务中，next token的生成含有大量重复的KV计算，KV cache随着序列生成逐步缓存KV，加快模型推理效率
这也就表明了KV cache的适用条件

自回归生成任务：token是逐步生成的，不能访问未来信息(区别于encoder模型(BERT)和传统Transformer模型(含有非掩码的multi-head attention))
因果注意力(Causal Attention): 只依赖于 previ ous token

在推理过程，计算next token时，L个Transformer block的中间结果需要被重复利用
将Key, Value缓存起来加速推理

Why KV Cache

推理实际上是什么样的
如果没有KV Cache，每一次注意力的计算都需要计算到目前为止所有token的QKV矩阵，进行矩阵运算
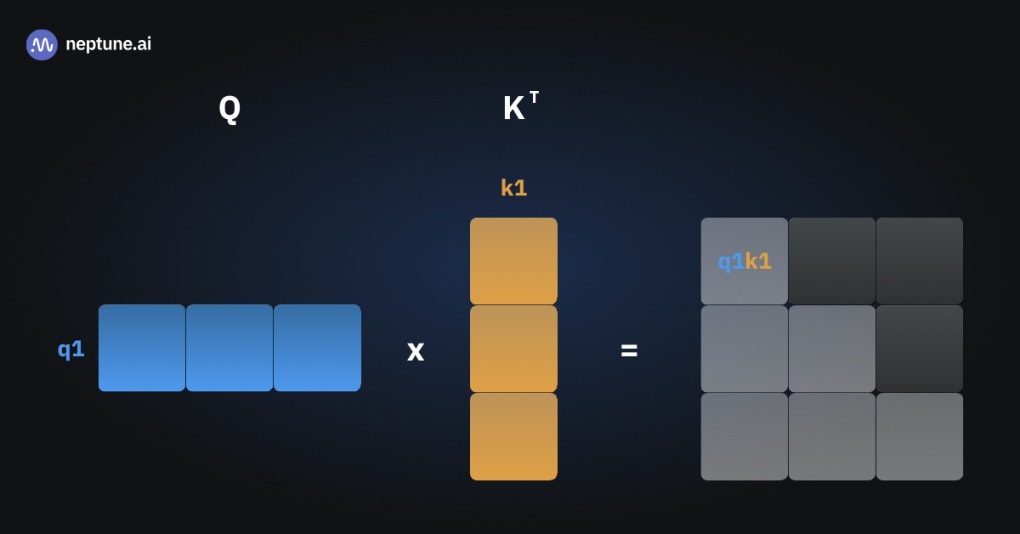
Pasted image 20250126152152
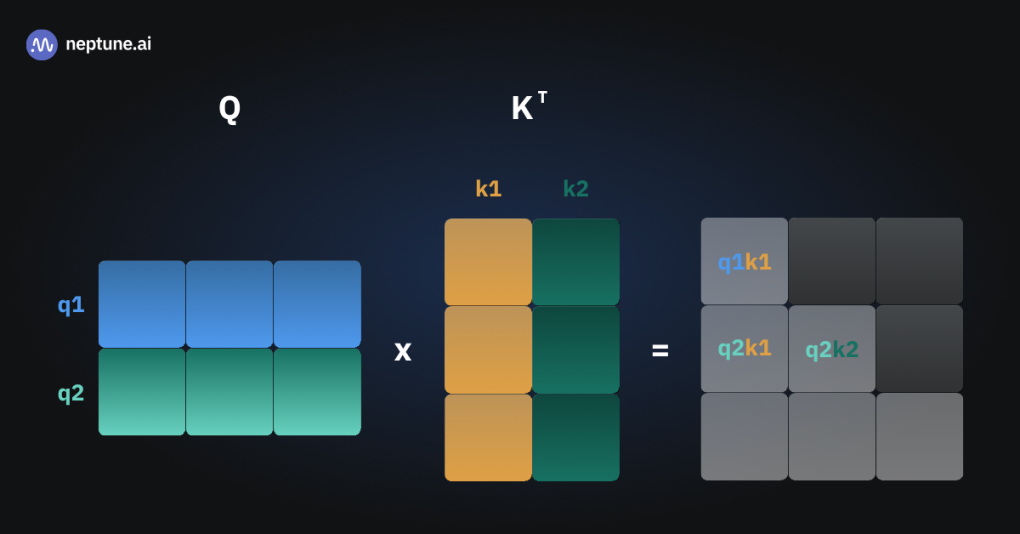
Pasted image 20250126152204
Pasted image 20250126150457

图片来自 Transformers Key-Value Caching Explained

三张图片表示三次推理，可以看到有多次的重复运算
如果能够将中间过程的状态缓存起来，那每一次就只需要计算新token的Key 和 Value，与缓存的K，V连接，就能计算所需的注意力矩阵

Why it Works

听上去很合理，但是仔细一想可能会感觉有点奇怪
以下是几个可能的问题

第一层进行缓存十分合理，KV只取决于权重矩阵，输入是原始输入的token序列，KV在每一次都保持不变，但是hidden state也可以如此吗？
- Decoder-only 模型所有的注意力块都是masked multi-head attention，注意力矩阵都是一个下三角，无注意力部分不参与计算
- 在每一次attention matrix与Value matrix相乘的时候，结果(理解为下一层输入)矩阵的每一行，由attention matrix决定。attention matrix是一个下三角，掩盖了未来的token，也就使得结果的每一行都是之前的token和本身的token 的 V 的加权和
- 新token不参与当前token对应输出的运算
- 每一次的输出都是一样的，缓存是可行的
既然每一次旧token的输出都是一样的，为什么要计算整个矩阵而不是求解新向量
- 加入KV Cache后，就只需要通过已经缓存的矩阵与新token的 QKV计算新token的输出就可以
既然只需要求一个新向量，旧token的输出都相同，为什么不缓存输出
- 计算新token的输出是 $a \times V$ ，其中 $a$ 是新token与 $K$ 计算得到的注意力向量， $V$ ，哪怕缓存旧输出，新输出的计算仍然需要 K V 矩阵
为什么不对Q进行缓存
- 进行KV Cache 后，整个推理过程只有新token的Q，K，V是新计算的，不再需要过往的Q

相关技术

通过粗略的计算可以得出
在没有KV Cache的时候，一次推理耗费的FLOPs大约为

n \times (24 b s h^{2} + 4 b s^{2} h) + 2 b s hV

在有KV Cache的时候，一次推理耗费FLOPs大约为

n \times (24 b h^{2} + 4 bh + 4 b (K V_{-} L e n g t h)) + 2 bhVh

可以看出快了许多

但是KV Cache随着序列的长度增加而增大，使得原本计算集中型问题变成IO集中型问题。对显存(HBM)要求很大，如何减小缓存使用是KV Cache的核心问题

KV Cache显存的计算方法

1 token = 2 [K, V] \times H \times N \times 2 bytes

其中 $H$ 为hidden state， $N$ 为层数

优化的方法可分为四类

共享KV：多个Head共享KV，代表方法：GQA，MQA
窗口KV：维护一个KV cache 窗口，超出窗口被丢弃，优化KV存储但是可能损失一定的长文推理效果代表：Longformer
量化压缩：量化(如8bit)来保存KV，代表方法：INT8
计算优化：优化计算过程，减少访存换入换出的次数，让更多计算在SRAM上进行。代表方法：flashAttention

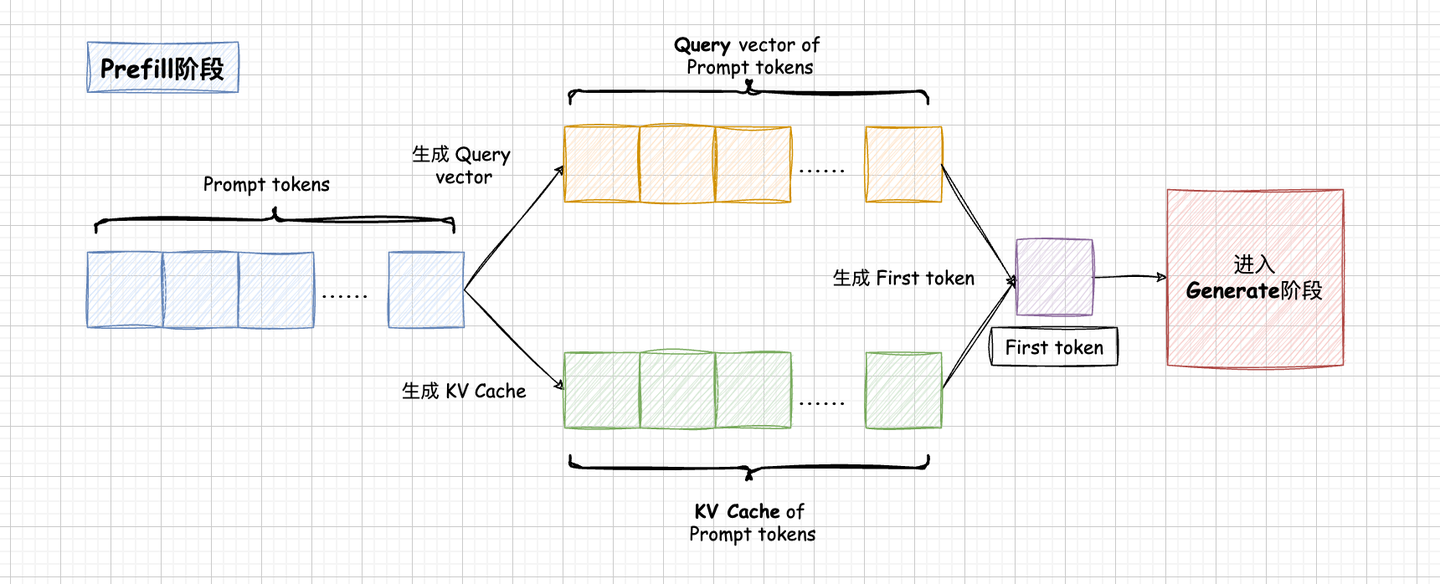
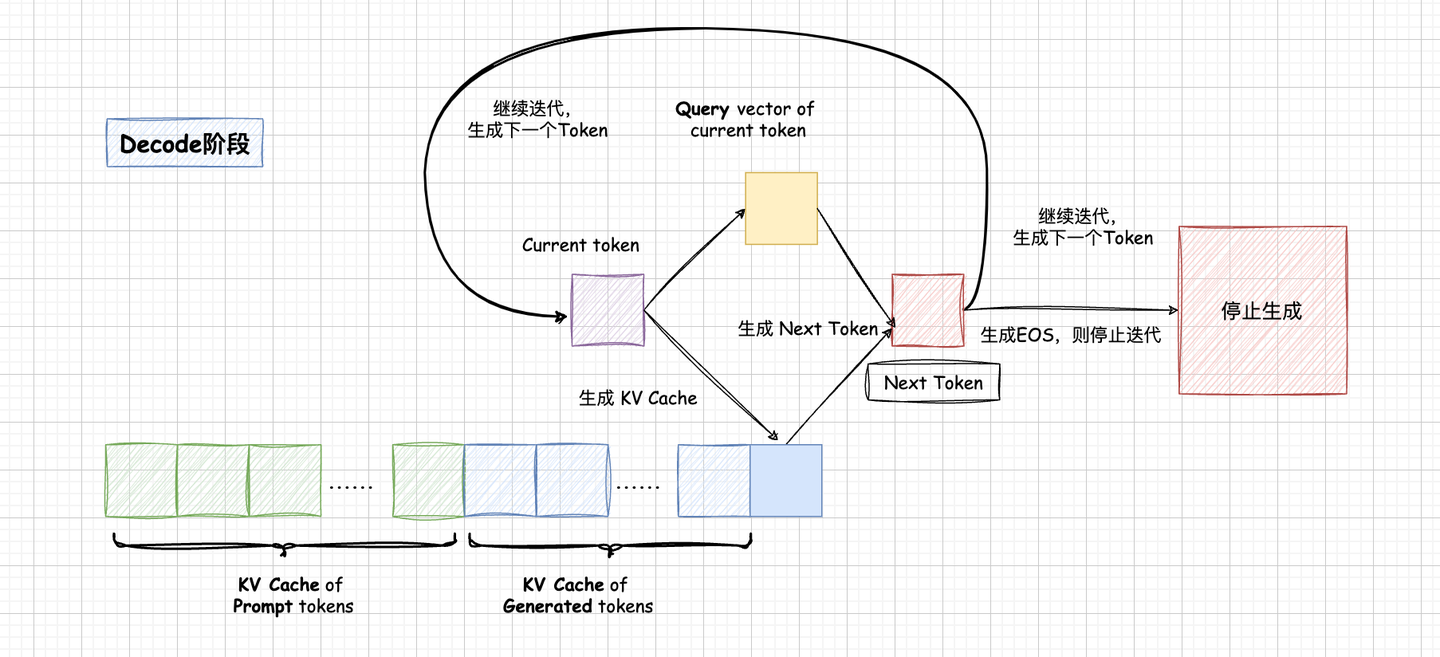
前置知识: Prefill 和 Decode

Prefill阶段对Prompr中所有token并行计算，得到Prompt token的KV Cache 和首token
Decode阶段使用Prefill得到的KV Cache自回归生成并逐步累积KV Cache

Pasted image 20250126165302
Pasted image 20250126165309

图像来自 KV Cache优化🔥MQA/GQA/YOCO/CLA/MLKV笔记: 层内和层间KV Cache共享

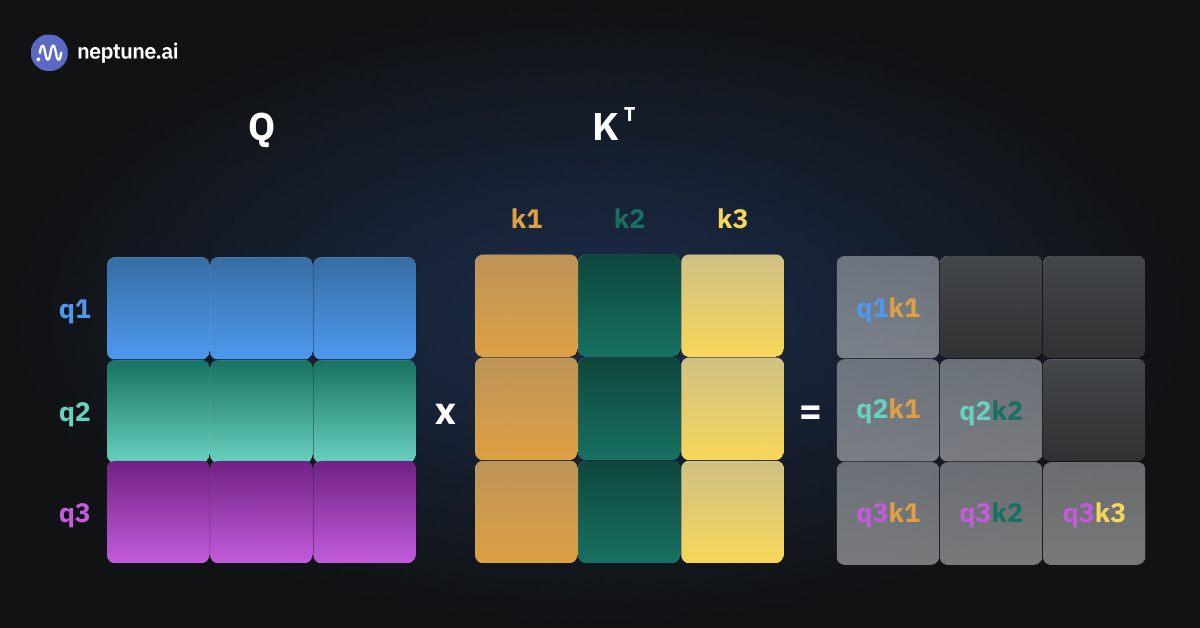
MHA(Multi-head Attention)

多头注意力机制，每一个token有多个KV head 和 Query head
随着层数增加，需要缓存大量的KV，导致计算和IO快速增加

显存

1 token = 2 [K, V] \times H \times N \times 2 bytes

一共是 $2 \times l \times n_{h}$ 个 $k, v$

MQA(Multi-Query Attention)

1911.02150

保留一个KV head，多个Query heads共享相同的KV head
一个token的不同head的Attention 差异只在Query上
极大地降低了KV Cache的需求，但是导致模型效果下降

MQA将KV Cache减少到原来的 $1/ h$ ，其中 $h$ 是head数量。在共享K, V后，Attention参数减少了将近一半，通常会增加FFN/GLU(Gated Linear Unit, a type of activation function)参数来保证参数不变。支持者相信可以通过更多的训练来优化使用MQA的模型效果

使用MQA的模型包括 PaLM, Gemini等

显存

1 tokens = 2 [K, V] \times H / N_{h} \times N \times 2 bytes

其中 $N_{h}$ 是Head数量

一共是 $2 \times l$ 个 $k, v$

GQA(Grouped-Query Attention)

2305.13245

GQA将Head分成g个组，每组共享一对K, V

使用GQA的模型包括 Llama2-70B, Llama3, DeepSeek-V1, Yi, ChatGLM2, ChatGLM3…
GQA的 g(分组数)通常设置为8，可能的原因是当体量大于单张卡时，用单机(8卡)部署，一张卡负责一个KV head

显存

1 token = 2 [K, V] \times H / N_{h} \times G \times N \times 2 bytes

其中 $G$ 是组数

一共是 $2 \times l \times g$ 个 $k, v$

MLA(Multi-head Latent Attention)

deepseek-v2, v3使用的技术

Intro

MLA 完整公式

只缓存蓝色框的向量 $c_{t}^{K V}, k_{t}^{R}$
其中

$c_{t}^{K V}$ 维度为 $d_{c} = 4 \times d_{h} = 512$
$k_{t}^{R}$ 维度为 $d_{h}^{R} = d_{h} /2 = 64$

比起MQA增加了2.25倍存储，报告中声称优于MHA

Notation

$d_{c}$ ：是MLA低秩压缩的维度，论文中为 $4 d_{h}$

$d_{h}$ : 是head size

$n_{h}$ : 是每层head的数量

$d$ : 隐层维度， $d = d_{h} \times n_{h}$

$W^{DK V} \in R^{d_{c} \times d}$ : 低秩变换矩阵

Details?

对于KV的计算

对输入 $h_{t}$ 做一个低秩压缩，将 $d$ 维德输入经过 $W^{DK V}$ 变换后压缩成 $d_{c}$ 维的 $c_{t}^{K V}$
DeepSeek-V3中， $d = 7168, d_{c} = 512$
即公式(41)

c_{t}^{K V} = W^{DK V} h_{t}

然后再通过两个变换矩阵将KV的维度扩展回到 $d$ ，即公式(42, 45)

[k_{t, 1}^{C}; k_{t, 2}^{C}; ...; k_{t, n_{h}}^{C}] = k_{t}^{C} = W^{U K} c_{t}^{K V}

[v_{t, 1}^{C}; v_{t, 2}^{C}; ...; v_{t, n_{h}}^{C}] = v_{t}^{C} = W^{U V} c_{t}^{K V}

这样的变换十分类似于LoRA的做法。LoRA通过压缩-扩展实现了参数量的减少，MLA这样也实现了参数量的减少，但是这里的目的是减少KV Cache。此时实际参与计算的KV和原来是一样的，而且还多了一步计算。

对于Q的计算

与KV类似进行压缩-扩展的操作，即公式(37, 38)

c_{t}^{Q} = W^{D Q} h_{t},

[q_{t, 1}^{C}; q_{t, 2}^{C}; ...; q_{t, n_{h}}^{C}] = q_{t}^{C} = W^{U Q} c_{t}^{Q},

V3中 $d_{q} = 1536$ ，可以理解为减少参数量？

RoPE的处理

单独计算了两个位置编码 $q_{t}^{C}$ , $k_{t}^{C}$

[q_{t, 1}^{R}; q_{t, 2}^{R}; ...; q_{t, n_{h}}^{R}] = q_{t}^{R} = RoPE (W^{QR} c_{t}^{Q}),

k_{l}^{R} = RoPE (W^{K R} h_{l}),

此处的 $q_{t, i}^{R}, k_{t}^{R}$ 的维度是 $d_{h}^{R}$ ，DeepSeek选择head size 的一半 $d_{h}^{R} = d_{h} /2 = 64$ 将两个位置编码接到对应的Q和K向量后

q_{t, i} = [q_{t, i}^{C}; q_{t, i}^{R}],

k_{t, i} = [k_{t, i}^{C}; k_{t}^{R}],

注意不是接到整个向量后面，在这里两个位置编码是共享的，使得 $k_{t}^{R}$ 与MQA类似被所有Head共享

这么做是为了什么？使用低秩计算来降低KV的维度实现对KV cache 的优化是MLA的目的，但是RoPE 与低秩KV不兼容

如果不加RoPE

attention计算过程可以使用矩阵吸收计算(经过结合律，将前一个矩阵吸收到后一个矩阵中)处理

q_{t, i}^{T} \times k_{j, i} = (W_{(i)}^{U Q} c_{t}^{Q})^{T} \times W_{(i)}^{U K} c_{j}^{K V} = (c_{t}^{Q})^{T} \times (W_{(i)}^{U Q})^{T} W_{(i)}^{U K} \times c_{j}^{K V}

方框中的部分是权重矩阵，相乘结果固定，可以提前计算。此时便只需要缓存 $c_{j}^{K V}$ (维度为4 $d_{h}$ ，远小于 $d$ ，原文中 $d = 64 d_{h}$ )，就可以实现KV cache

如果加上RoPE

RoPE的矩阵会夹在 $W^{U Q}$ 和 $W^{U K}$ 之间

q_{t, i}^{T} \times k_{j, i} = (R_{t} W_{(i)}^{U Q} c_{t}^{Q})^{T} \times R_{j} W_{(i)}^{U K} c_{j}^{K V} = (c_{t}^{Q})^{T} \times (W_{(i)}^{U Q})^{T} R_{t}^{T} R_{j} W_{(i)}^{U K} \times c_{j}^{K V} = (c_{t}^{Q})^{T} \times (W_{(i)}^{U Q})^{T} R_{t - j} W_{(i)}^{U K} \times c_{j}^{K V}

$(W_{(i)}^{U Q})^{T} R_{t - j} W_{(i)}^{U K} \times c_{j}^{K V}$ 随着位置变化而变化，无法单纯通过缓存 $c_{j}^{K V}$ 得到 attention

MLA的处理

通过在每一个Head的向量 $q_{t, i}^{C}, k_{t, i}^{C}$ 后面加上小维度( $d_{h}^{R}$ )的向量 $q_{t, i}^{R}, k_{t}^{R}$ 来表示位置信息
对于 $q_{t, i}^{R}$ 来说，每一个Head位置均不相同，对于 $k_{t}^{R}$ 来说，相当于使用MQA进行K的cache，所有Head共享一个K

将一个Head的Attention计算过程分为两步

q_{t, i}^{T} \times k_{j, i} = [q_{t, i}^{C}; q_{t, i}^{R}]^{T} \times [k_{j, i}^{C}; k_{t}^{R}] = q_{t, i}^{C} k_{j, i}^{C} + q_{t, i}^{R} k_{t}^{R}

前面部分使用矩阵吸收计算，后面使用MQA计算

则到这里便实现了低秩KV和RoPE的兼容

在这种实现方式下，需要缓存用于矩阵吸收计算的 $c_{t}^{K V}$ ，还需要额外保存用于MQA的 $k_{t}^{R}$

$c_{t}^{K V}$ 维度为 $4 \times d_{h} = 512$
$k_{t}^{R}$ 维度为 $d_{h} /2 = 64$

Summary

MLA是一种低秩KV的实现方式，通过低秩压缩和扩展，保存小维度的KV优化存储，也保持了恢复原维度的能力。按理说可能比MQA，GQA更有优势。
MLA实际上也增加了模型的计算量，在苏神的文章中认为带宽瓶颈更为突出，所以速度仍有提升。
比较有意思的一点是，MLA架构下，KV cache与Head number $h$ 没有关系，所以才会看到惊人的 $h = 64, h = 128$ 等设计。这样的设计直觉上能够增强模型的能力，不知事实是否有体现。

White Box

Notes

Flash Attention

PagedAttention

Positional Embedding

Thoughts

当我第一次试着谈论死亡

Strange Thoughts on Coffee