Flash Attention

Overview

FlashAttention: 利用SRAM，通过数学tricks将矩阵拆分成块，以减少HBM访问次数

The paper title: FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness
It means that FlashAttention is:

• Fast
• Memory-efficient: compare to $O(N^2)$ of the vanilla attention, FlashAttention is sub-quadratic(次二次，增长小于二次但是大于线性)/linear in $N(O(N))$
• Exact: Not an approximation(sparse, low-rank).
• IO aware: utilize the knowledge of the memory hierarchy

Preliminaries

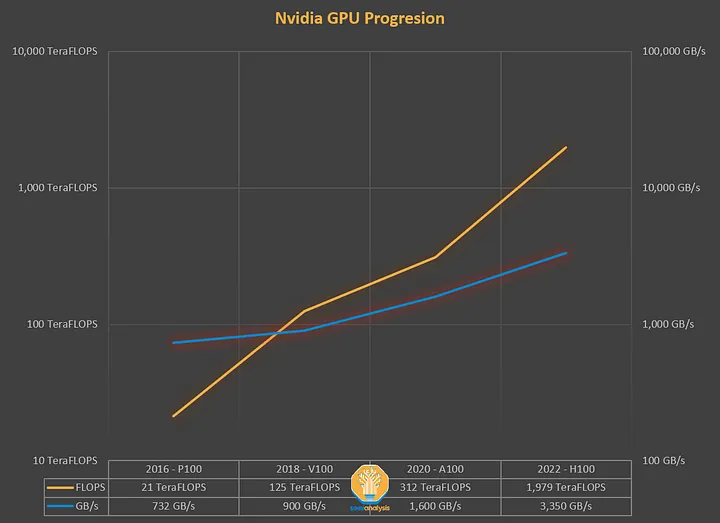
Excerpt from the blog: Over the years GPUs have been adding compute capacity at a faster pace than increasing the memory throughput(TB/s). It doesn’t matter if you can compute at exaFLOPS speeds if there is no data to be processed.

IO could be the main problem

Depending on the ratio between computation and memory accesses(commonly measured by the arithmetic intensity), operations can be classified as:

• compute-bound(matrix multiplication)
• memory-bound(elementwise ops(activation, dropout, masking), reduction ops(softmax, layernorm, sum…))

The computation of attention is memory-bound: it is elementwise operations or it has low arithmetic intensity

One way to tackle memory-bound ops is leverage the knowledge of memory hierarchy

GPUs as example

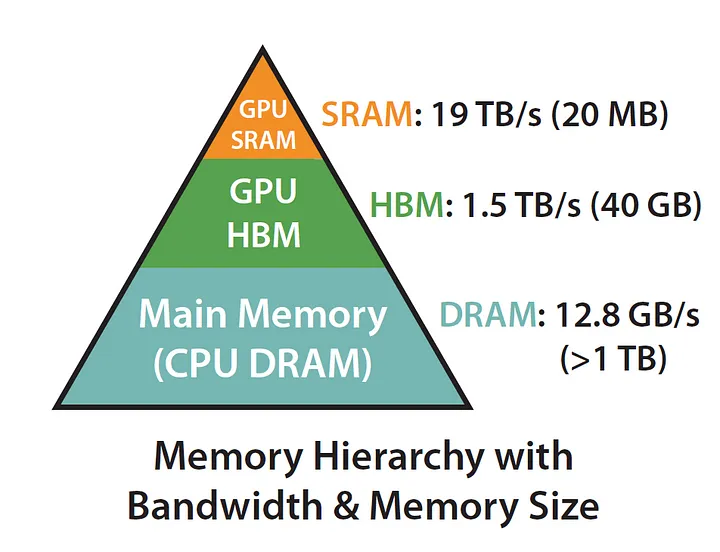
the faster the memory, the more expensive it is, and the smaller its capacity

A100 GPU has 40–80GB of high bandwidth memory (HBM, the thing that gives you lovely CUDA OOMs) with a bandwidth of 1.5–2.0 TB/s and 192KB of on-chip SRAM per each of 108 streaming multiprocessors with bandwidth estimated around 19TB/s(108个streaming multiprocessors每个有192KB的on-chip SRAM，共计20MB).

Since SRAM is far faster than HBM, we could keep some data in SRAM and reduce write and read ops from HBM.

To exploit the tircks, we should understand how standard attention computes

• vallina attention treats HBM load/store ops as 0 cost.
• write S, read S for softmax, write P and read it again, these IO ops could be unnecessary/redundant
• we could perform all of the intermediate steps in SRAM without redundant IO

The method that keep that keep intermediate result/steps(fusing multiple ops together) in the high speed memory called kernel fusion(核聚变)

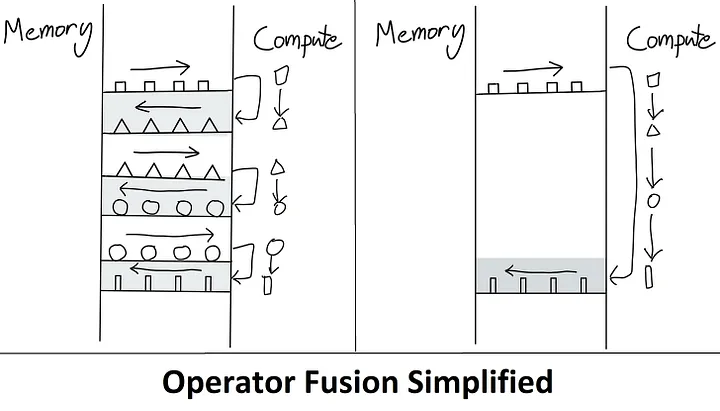
A kernel is basically a fancy way of saying “a GPU operation”

FlashAttention

Flash attention boils down(归纳为) to 2 main ideas

• Tiling(both forward and backward passes) — chunking the $N\times N$ softmax/scores matrix into blocks.
• Recomputation(backward only)
  • similar to activation/gradient checkpointing

activation/gradient checkpointing 是一种缓存部分激活值(而非全部)以减少内存使用的优化技术 大概的内容是
在模型训练时，通常会在前传时计算并存储所有层的激活值，在反向时计算梯度，当模型深度增加时，这些激活值会占用大量内存
activation/gradient checkpointing 只保存关键层的激活值(checkpoints)，在需要时重新计算来得到梯度，减少内存使用的同时也额外增加了计算量

Step 0: allocating Q,K,V matrices in HBM $N$个token，$d$维embedding，SRAM大小为$M$ Step 1: initialize the block size. 为什么是$\frac{M}{4d}$ 上取整？为了最大化地利用SRAM大小，SRAM大小为M，而算法每次进行运算需要维护四个block: 分别对应q, k, v, o(output)。所以$B_c,B_r$(列大小，行大小)都与$\frac{M}{4d}$相关。而为什么$B_r$是$d$ 和上取整取min？根据原作者的说法，这是为了让块的大小不超过 $M/4$(见[Question] Does the order of for-loop matter? · Issue #766 · Dao-AILab/flash-attention)

有一些比较不清楚的点可能得从实际实现上回答

• 为什么是上取整？如果每个都略大于$M/4d$，最终会超过on-chip SRAM的大小，是否是因为略超过带来的communication影响并不大所以允许
• 为什么是on-chip？是为了避免SRAM间的交流吗？

Step 2: initialize $O,l,m$. $O$ 是注意力层的最终输出(多次迭代后得到)，$O$是一个矩阵(多个token的输出)。$l$ 维护相对于块的softmax 分母(exp sum)，$m$维护块中各个token的logit最大值，$l,m$都是向量，用于计算softmax。

为什么SRAM还能放得下$l,m$，博客的解释是register

Step 3: Divide Q, K, V. 将Q按块的行大小进行拆分，拆分为$(B_r,d)$的块($B_r$个token的q组成)，将K, V按列大小进行拆分，拆分为$(B_c,d)$的块($B_c$个token的k/v组成)。使得计算注意力之后，形成$(B_r,B_c)$大小的块存储在SRAM中

Step 4: Divide O, l, m，均拆分为 $T_r$ 个块

Step 5, 6: first loop 遍历K, V。从HBM中载入 $K_j,V_j$

Step 7, 8: second loop 遍历Q。从HBM中载入 $Q_i,O_i,l_i,m_i$

Step 9: On chip, compute $S_{ij}$ 即按块计算注意力分数 $S_{ij}=Q_i{K}_j^T$

Step 10: On chip, compute ${\tilde{m}}_{ij}$, ${\tilde{P}}_{ij}$, ${\tilde{l}}_{ij}$ 计算每个token注意力分数的最大值($m_{ij}$)，与注意力分数作差计算exp($P_{ij}$)，并计算exp之和($l_{ij}$)

Step 11: On chip, compute $m_i^{new}$, $l_i^{new}$ 与上一次迭代维护的$m_i,l_i$ 计算新的$m,l$。其中m取二者最大，$l_i^{\mathrm{new}}=e^{m_i-m_i^{\mathrm{new}}}{l}_i+e^{{\tilde{m}}_{ij}-m_i^{\mathrm{new}}}$

Step 12: Write new $O_i$ to HBM 计算新的$O_i$ 到HBM上 ${\mathbf{O}}_i\leftarrow \mathrm{diag}({\ell }_i^{\mathrm{new}}{)}^{-1}(\mathrm{diag}({\ell }_i)e^{m_i-m_i^{\mathrm{new}}}{\mathbf{O}}_i+e^{{\tilde{m}}_{ij}-m_i^{\mathrm{new}}}{\tilde{\mathbf{P}}}_{ij}{\mathbf{V}}_j)$

Step 13: Write new $m,l$ to HBM

Step 14,15,16: End loop, return $O$

粗略地理解，这样的算法将注意力的计算拆分为块的计算，使得与HBM的交互(IO上的成本)变小，中间计算更集中在SRAM与计算单元之间的交互，加快了注意力的计算

大致的流程可按下图理解

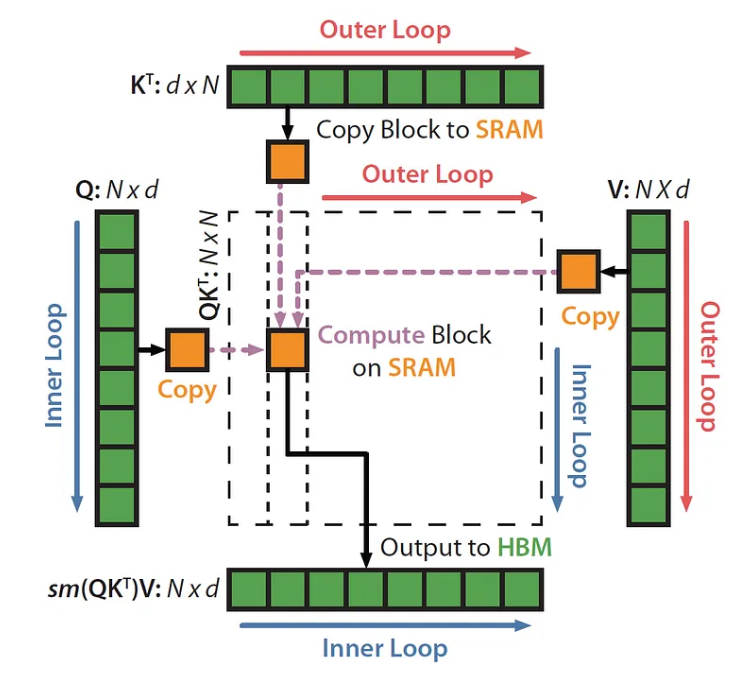
列方向的是第二层循环(即原本一个token的注意力分数结果)
行方向的是第一层循环
最终得到的是注意力块的输出(与V相乘并且softmax)
直到行方向的结束，当前token的输出才是正确值

更具体地
这个奇怪的计算过程(exp作差，m, l的维护，与上一次迭代结果的计算)是怎么回事？
首先，为什么会需要这样的过程？因为softmax。
softmax的计算，需要当前token作为q和所有dot product的结果。这需要所有的K都加入SRAM，得到结果后才能进行softmax。但是这显然是做不到的，SRAM并不足以放下所有的K和中间结果。这也是分块的目的，所以为了得到精确的softmax结果，我们需要一些数学方法
对于一个块，我们采用下面的计算方法

$$m(x):=\underset{i}{\max }{x}_i,f(x):=\left[e^{x_1-m(x)}\dots e^{x_B-m(x)}\right],\ell (x):=\sum _{i}f(x{)}_i,\mathrm{softmax}(x):=\frac{f(x)}{\ell (x)}.$$

先忽略$m(x)$，这样的计算纯粹就是对当前能得到的logit，计算一次softmax而已
很关键的一点是，softmax的计算是各个logit的exp除以一个常数，所以对于两个块的计算结果，我们只需要消去常数的影响，再除以常数之和就可以

$$m(x)=m(\left[x^{(1)}{x}^{(2)}\right])=\max (m(x^{(1)}),m(x^{(2)})),f(x)=\left[e^{m(x^{(1)})-m(x)}f(x^{(1)})e^{m(x^{(2)})-m(x)}f(x^{(2)})\right],$$ $$\ell (x)=\ell (\left[x^{(1)},x^{(2)}\right])=e^{m(x^{(1)})-m(x)}\ell (x^{(1)})+e^{m(x^{(2)})-m(x)}\ell (x^{(2)}),\mathrm{softmax}(x)=\frac{f(x)}{\ell (x)}.$$

这就解释了维护上一次迭代结果的原因，对于每一次结果，我们需要维护$m,l,O_i$才能最终得到正确值
在实际运算中，算法先与V相乘再计算了softmax，优化了中间过程
而在消去常数的影响中，算法使用矩阵乘法，对于维护的$l$，取其对角阵$diag(l)$，实际上就是对每一行乘以对应的加和

然后，为什么需要作差？ 为了数值的稳定性。作差对结果并无影响，但是不作差的话，指数运算的结果可能过大，导致溢出或精度损失。减去最大值可以避免这种不稳定性。这个作差也通过中间指数运算进行消除和引入

The algorithm can be easily extended to “block-sparse FlashAttention”. By doing this we can skip nested for and scale up sequence length

Supplement

about complexity

Space:

• standard attention need $O(N^2)$ for space
• FlashAttention: Q, K, V, O are $(N,d)$ matrices, l, m are $N$ dim vectors. That’s $4Nd+2N$ in total. d usually samller than N, so we get $O(N)$ complexity for space

Time:

• measure by HBM accesses
• standard attention need $\Omega (Nd+N^2)$
• FlashAttention access HBM to load blocks. $N/(M/4d)$ blocks and two loops, we get $O(N^2{d}^2/M^2)$, but we could not load all the blocks at once, each time we load M data. And therefore the result become $O(N^2{d}^2/M)$
• for typical number in real world, FlashAttention leads up to 9x fewer accesses

about batch size, num_heads, backward pass

Batch size & num_heads
So far the algorithm is basically handled by a single thread block. This thread block is executed on a single streaming multiprocessor(SM). To extend the algo on larger scale, we just run $batch\_size\times num\_heads$ threadblocks in parallel on different SMs

If the number is bigger than the number of available SMs, the CUDA runtime use some sort of queues to implement the logic

这里有一个问题
如果按现在的做法，先迭代KV，再迭代Q，每一个token的计算都是被拆分的。必须先计算出当前的q对应的各个k中最大的m(1-j个块)，才能计算后面的块。也就是哪怕现在分成多个thread block，每个SM之间也得有交流(具体怎么做并不清楚)。也就是说必须一个序列一个thread block。 有没有可能一个序列也能使用多个thread block计算呢？
只需要将循环顺序交换就可以，先遍历Q，每个token的计算就变成独立的。不同token就可以放在不同thread block计算。也就是FlashAttention v2中的一个改进

backward pass & recomputation

反向传播比较复杂。
标准的attention会在前传时存储$P$用于计算梯度，P是一个$O(N^2)$的矩阵，而FlashAttention需要S和P计算梯度，在反向传播时使用QKV重新计算S, P(recomputation)
同样进行tiling

更具体得参考论文和公式推导

• FlashAttention v1、v2 - 公式推导 && 算法讲解
• FlashAttention 反向传播运算推导
• LLM（十七）：从 FlashAttention 到 PagedAttention, 如何进一步优化 Attention 性能

References

• ELI5: FlashAttention. Step by step explanation of how one of… | by Aleksa Gordić | Medium 👈 mainly 好文推荐
• Flash Attention (Fast and Memory-Efficient Exact Attention with IO-Awareness): A Deep Dive | by Anish Dubey | Towards Data Science
• Flash Attention
• [2205.14135v2] FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness
• [2307.08691] FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning