Linear Classifier
一个未曾想过的可解释性方法，使用线性回归进行分类，权重矩阵每个行向量对应一个类别的分类权重，每个行向量与最终得到的X进行内积得到分类结果，则行向量一定包含着某种匹配信息
其中，say，，则可以将权重矩阵每个行向量转化回图片的形式可以观察到这种匹配信息
内积接近于相似度，所以可能结果是
单层的线性回归就只能使用这样一个单一的模板
从高维空间来看，这些行向量/参数构成的直线划分了每个类别
Regularization and Optimization
存在一些recognition challenges: illumination(灯光，照明)，Deformation(变形), Occlusion(闭塞)，Clutter(混乱)，Intraclass Variation(同类别的不同)
SGD的一些问题
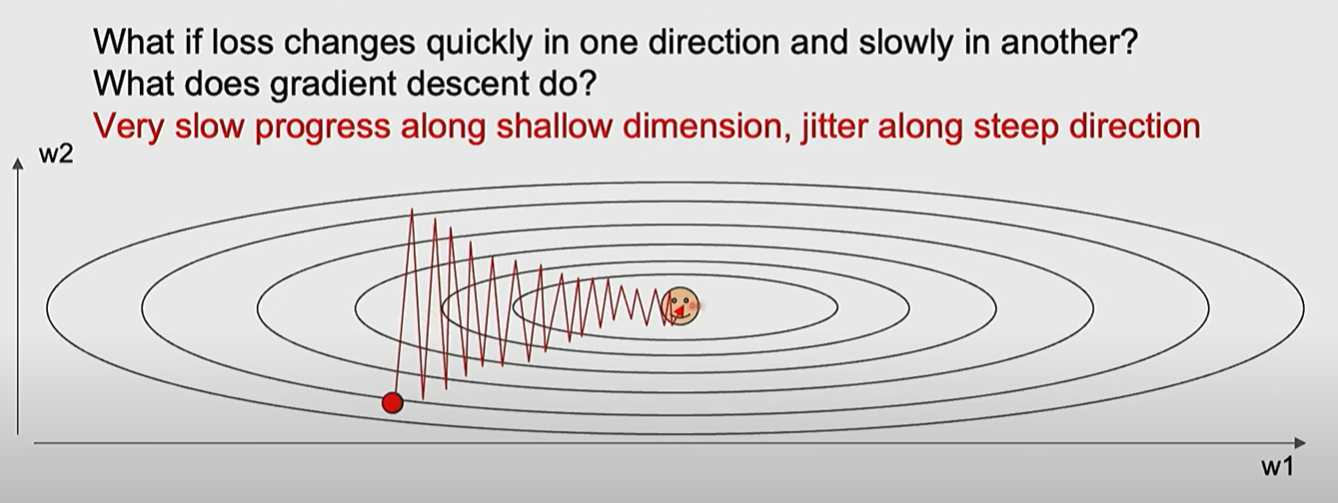如果梯度更新的时候，在一个方向上更新很快在另一个方向上更新很小，会导致振荡和收敛缓慢
略微数学视角的讲，如果损失函数的条件数(condition number)很高，即海森矩阵的最大奇异值与最小奇异值之比很大，则会发生这样的情况
第二个问题是 local minima和saddle point(鞍点)
第三个问题是 mini batch带来的噪声
条件数补充
海森矩阵是二阶导矩阵
条件数是海森矩阵最大奇异值与最小奇异值的比值，如果这个比值很大，意味着在一些方向上，梯度变化很大/曲率很大，在一些方向上则梯度变化很小/曲率很小，形成细长的椭圆/狭长的山谷的形状，出现上述的情况
多数情况中，海森矩阵是对称的，其奇异值等于特征值的绝对值 奇异值描述了梯度在某个方向上变化的剧烈程度
RMSProp
RMSProp增加了对梯度/学习率的调整，计算梯度平方的running average，每次更新时更新量除以这个running average的根号，使得对于大梯度采取较小的步长，小梯度采取大的步长
Adam
momentum + RMSProp
更新的是带有momentum的梯度，同时计算了学习率的变化，最后对二者进行bias correction进行调整
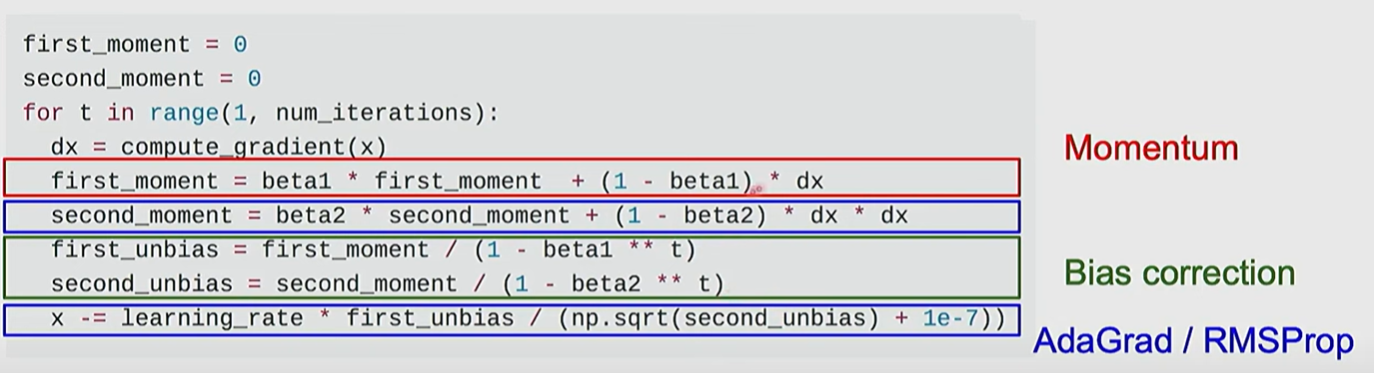
bias correction的目的主要是避免极端小的数值出现，经过乘除后可能出现极端情况
AdamW
传统Adam将regularization包含在loss function中，而AdamW把regularization放在最后更新处
这样使得loss function单纯的就是损失而不包含权重
Learning rate
If you increase the batch size by N, also scale the initial learning rate by N
2 order optimization
2阶优化要求更多的显存，更慢，通常结果会更好。
如果可以实现全batch训练，可以考虑二阶优化方式