李宏毅
Gradient Descent
参数的更新
但是有上百万的参数,高效的计算 -⇒ backpropagation
所以backpropagation就是梯度下降
数学基础
Chain Rule 微分链式法则
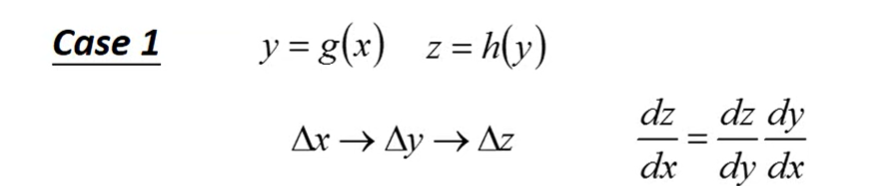

Backpropagation
Lost function
- 是对每一笔x(数据)定义的cost function,加和作为当前输出和目标的距离
求梯度
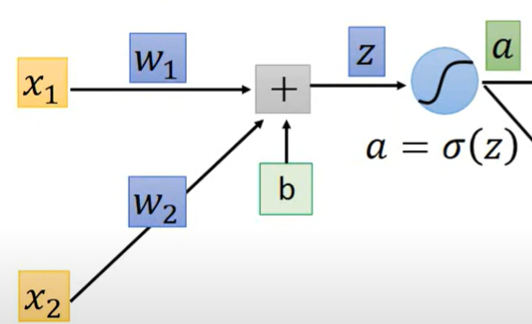
以线性神经元为例
对于单独一个线性神经元 有
z作为输入,传给激活函数
经过多层后输出,与 计算距离
- 称为 forward pass
- 称为 backward pass
Forward pass
结果就是各权重对应的输入
该权重的偏微分数值就是前一个神经元的输入
Backward pass
计算
z算完出来
过激活函数
如果是sigmoid
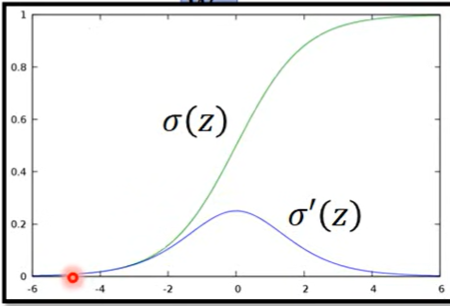
一层一层加
再加一层
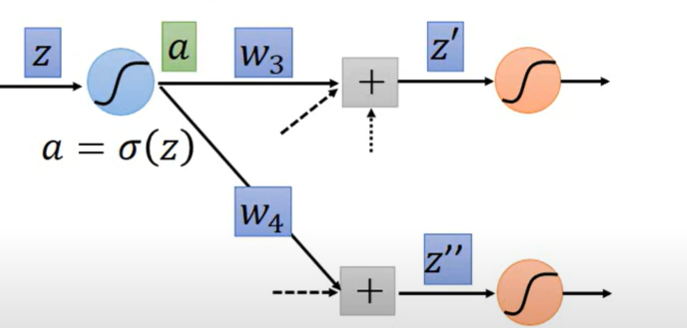
这个时候,C看成是 和 的某种加和 (chain rule)
这里只考虑了两个神经元,如果是多个就是多个链式相加 而且到这里都是在计算第一层权重系数中的某一个权重的梯度
到这里
假设后面两个偏导已经算出来了
此时可以有另外的角度看待这个式子
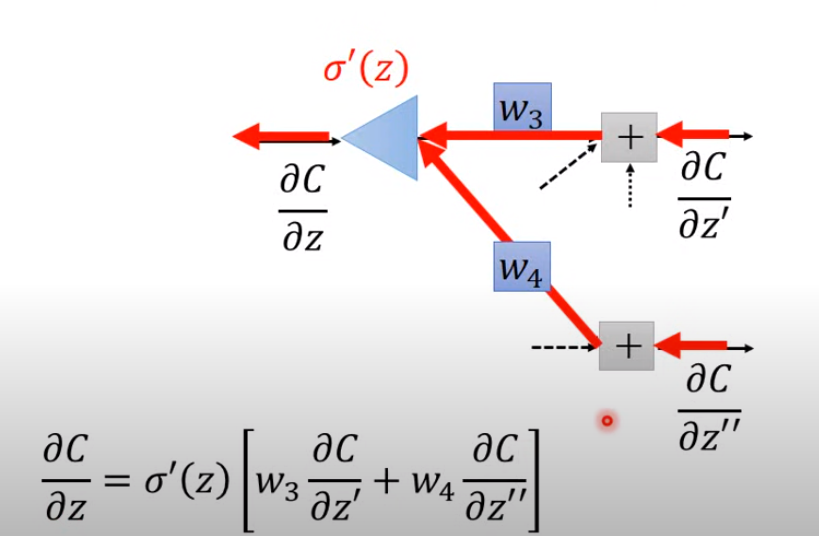 看成是输入 ,经过加和后乘上激活函数 得到输出就是
看成是输入 ,经过加和后乘上激活函数 得到输出就是
以微分的方式逆过来看
- 但是 已经在前面forward pass 决定了,所以现在是一个常数
然后
所以也是一个逆向的神经元输出,通过下一层的输入z的偏微分可以求出前一层的偏微分,最终给出权重的偏微分(compute recursively)
一直到输出层(output layer)
是激活函数输出,所以 就是激活函数的导在 上的取值
看损失函数怎么定义,直接对y求偏导就可以得到
所以秒算(李宏毅)
所以从最后一层开始往前算,一直到第一层就能得到梯度
所以此时变成
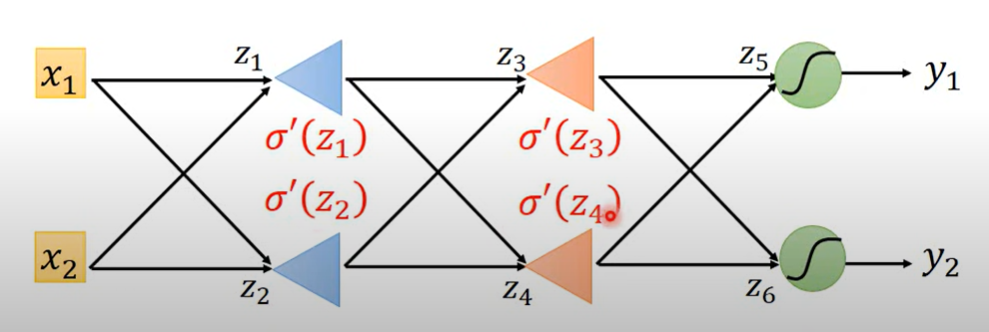
计算前一层的偏微分,就是后一层加权和,然后通过激活函数的导进行放大
- 输入是前向的
- 是个常数
总结
backpropagation 是梯度下降的算法,通过两个部分结合,逆向的计算梯度
backpropagation ()分为两个部分
一个是forward pass,一个是backward pass
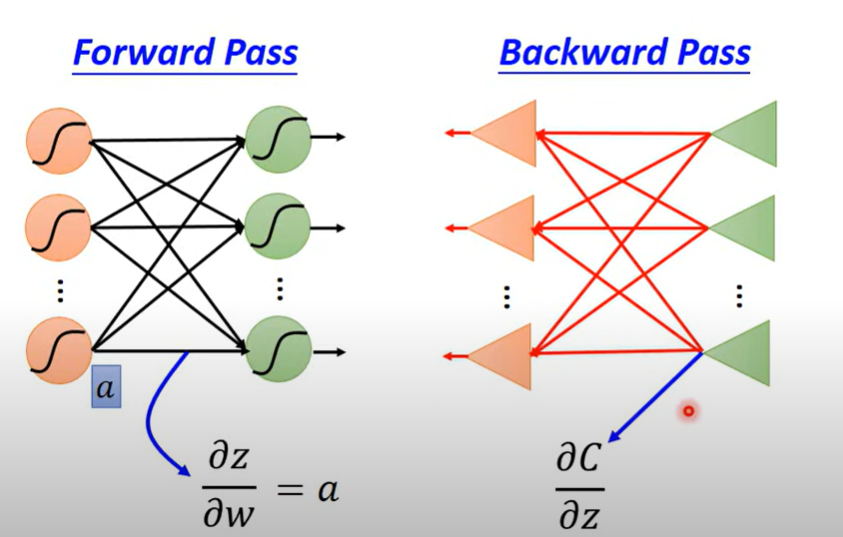
- forward pass () 就是指前一个激活函数输出到下一个激活函数输入的过程,也就是z,如何对参数求导的问题
- 结论是 每一层输入对参数的导都是前一层的输出
- backward pass () 是计算损失对输入的导的过程,将计算过程逆过来考虑,通过最后一层反向计算总体的损失对参数的导
- 这样的计算产生了激活函数导数的相乘(vanishing gradient problem)
- 反向和正向是等效的,只是这样比较有效且不复杂
- 两部分合起来构成了反向传播(相乘)
自己的补充
- 待补