References
- 【生成式AI】Diffusion Model 原理剖析 (1/4) (optional) - YouTube
- 【生成式AI】Diffusion Model 原理剖析 (2/4) (optional) - YouTube
- 【生成式AI】Diffusion Model 原理剖析 (3/4) (optional) - YouTube
- 【生成式AI】Diffusion Model 原理剖析 (4/4) (optional) - YouTube
浅谈Diffusion Model
Denoising Diffusion Probabilistic Model
DDPM
如何运作
从Gaussion distribution里sample出一个Vector
Dimension和目标图片大小一致
经过一个Denoise network,筛去一些杂讯,不断Denoise得到清晰的图片
denoise的次数是事先定好的,step从大到小
杂讯到图片的步骤,称为Reverse process
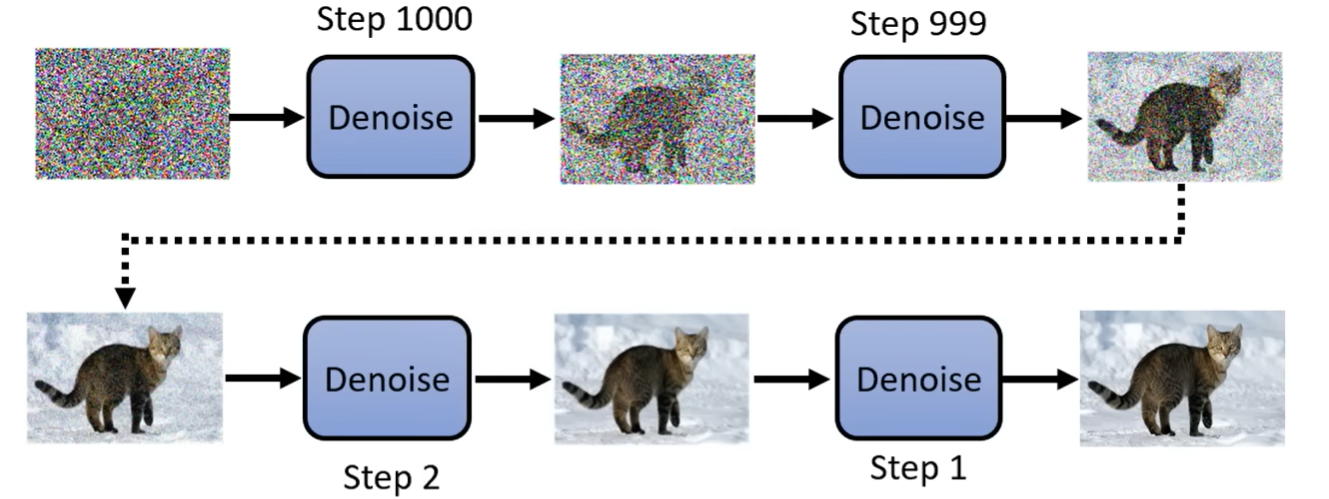
Denoise Model
输入除了杂讯图之外,还有杂讯的严重程度
这里denoise model一直是同一个
Noise predictor
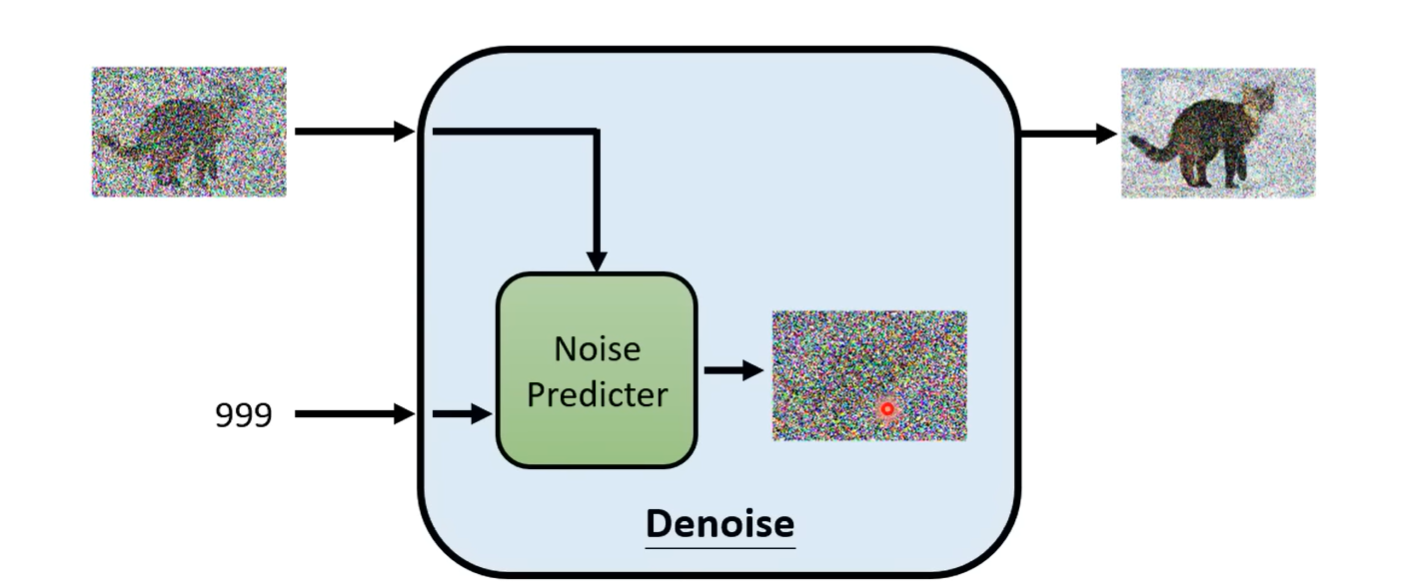 noise predictor 预测杂讯的样子,然后减掉输入的图片产生输出图片
noise predictor 预测杂讯的样子,然后减掉输入的图片产生输出图片
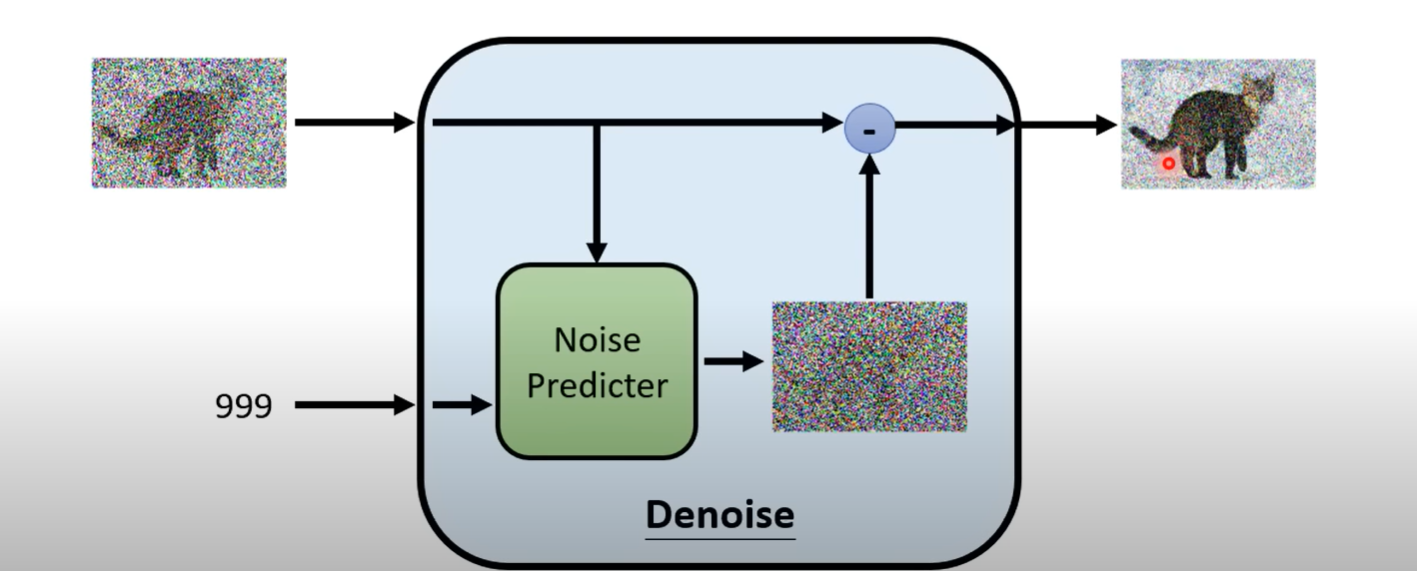
- 为什么不直接训练一个end-to-end model直接产生图片
- 这个可能比较简单
- 如果产生一个原图加杂讯,那模型基本就能画出原图了,不是很合理
- 有杂讯的图减去杂讯
- 但是会有很多不同情况,每一步去噪的输入噪声程度都不一样,怎么指明
- 加入step描述程度
Forward process/Diffusion Process
但是在训练时的ground truth怎么来
人为增加噪声
对dataset中的图片,人为sample Gaussion distribution中的噪声,一次次加,每一次加带有step数和噪声ground truth
这个过程称为diffusion process
Text-to-Image
文字生图仍然需要成对的资料
将文字也作为输入喂给Denoise模组(也就是给noise predictor)
几个流行模型介绍
大概架构
三个部分Text encoder, Generation model, Decoder
分开训练然后组合起来
Text encoder
对文字进行编码,喂给generation model
Generation Model
输入一个杂讯和文字向量,经过中间生成模型(一般是diffusion model)产生一个中间产物
中间产物是图片压缩的结果
可以是人类看得懂的也可以是人类看不懂的
Decoder
中间产物解码得到图片
Stable Diffusion
SD
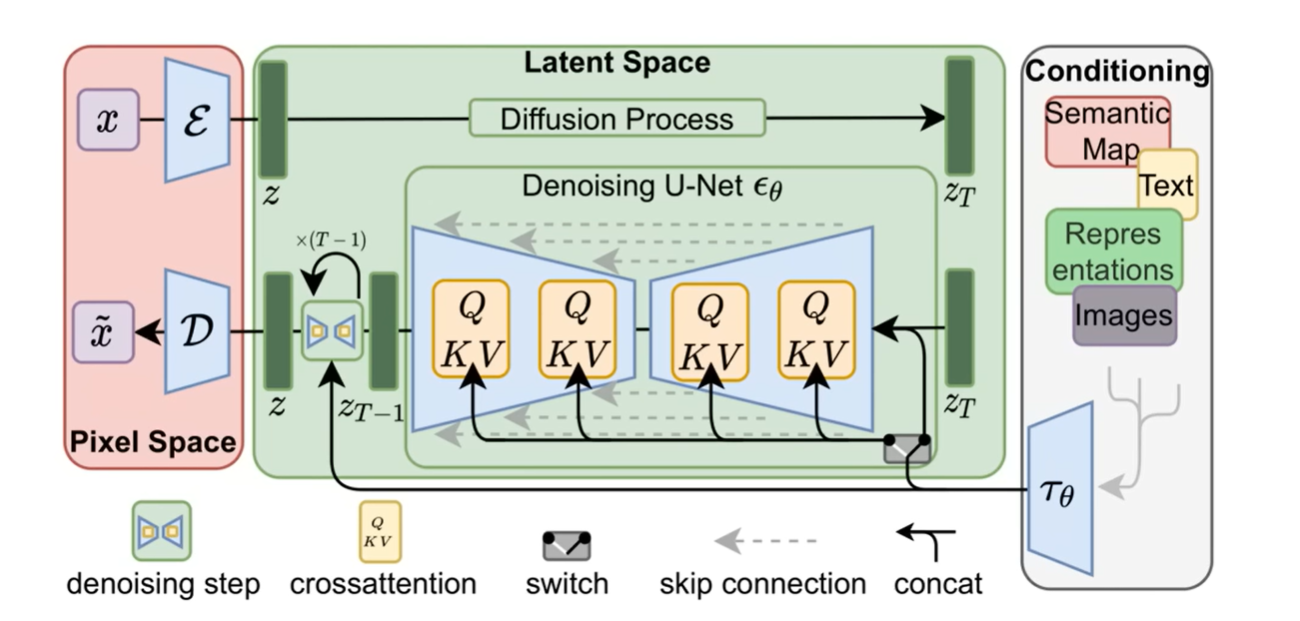
- 一个encoder,编码各种东西
- 经过diffusion model
- decoder解压缩
DALL-E
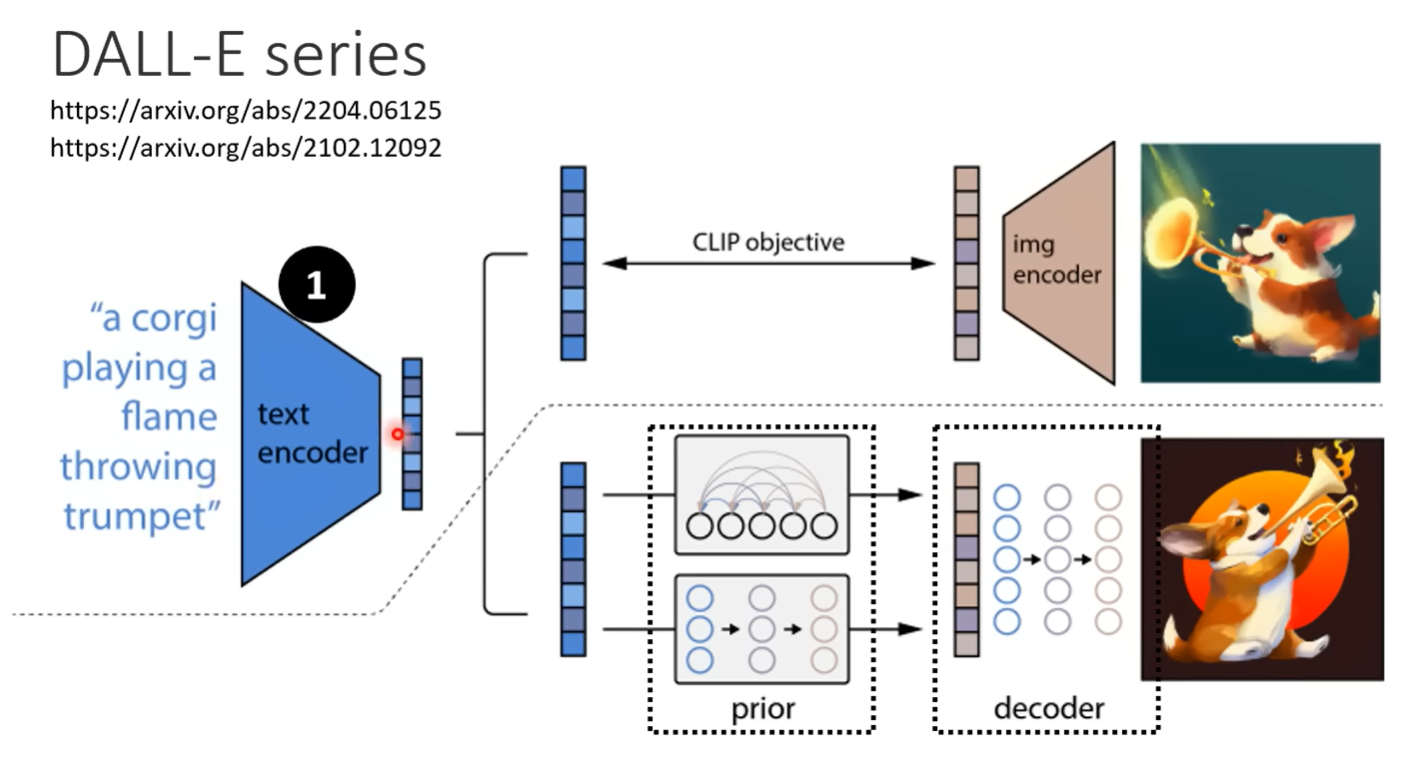
- encoder
- 文本encoder,图像encoder
- Autoregressive 运算量大,生成不完整的图(压缩的版本)
- Diffusion,生成完整的图片
- decoder还原图片
Imagen
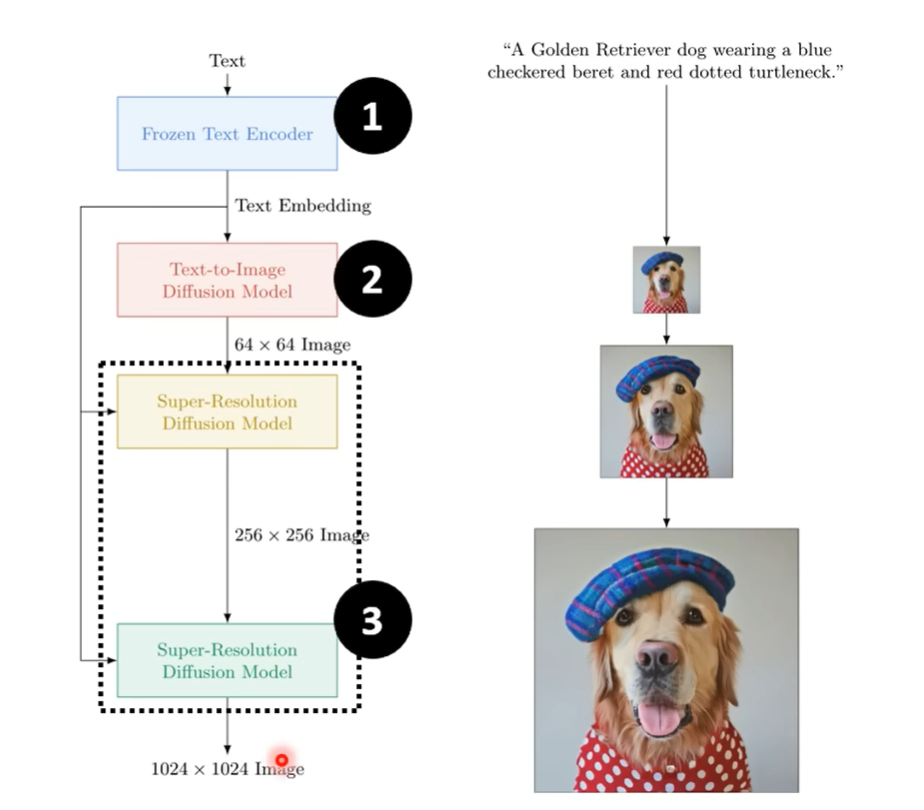
- encoder 编码文本向量
- diffusion model 生成一张不清晰的图
- decoder也是diffusion model,通过几次放大得到清晰图片
Encoder
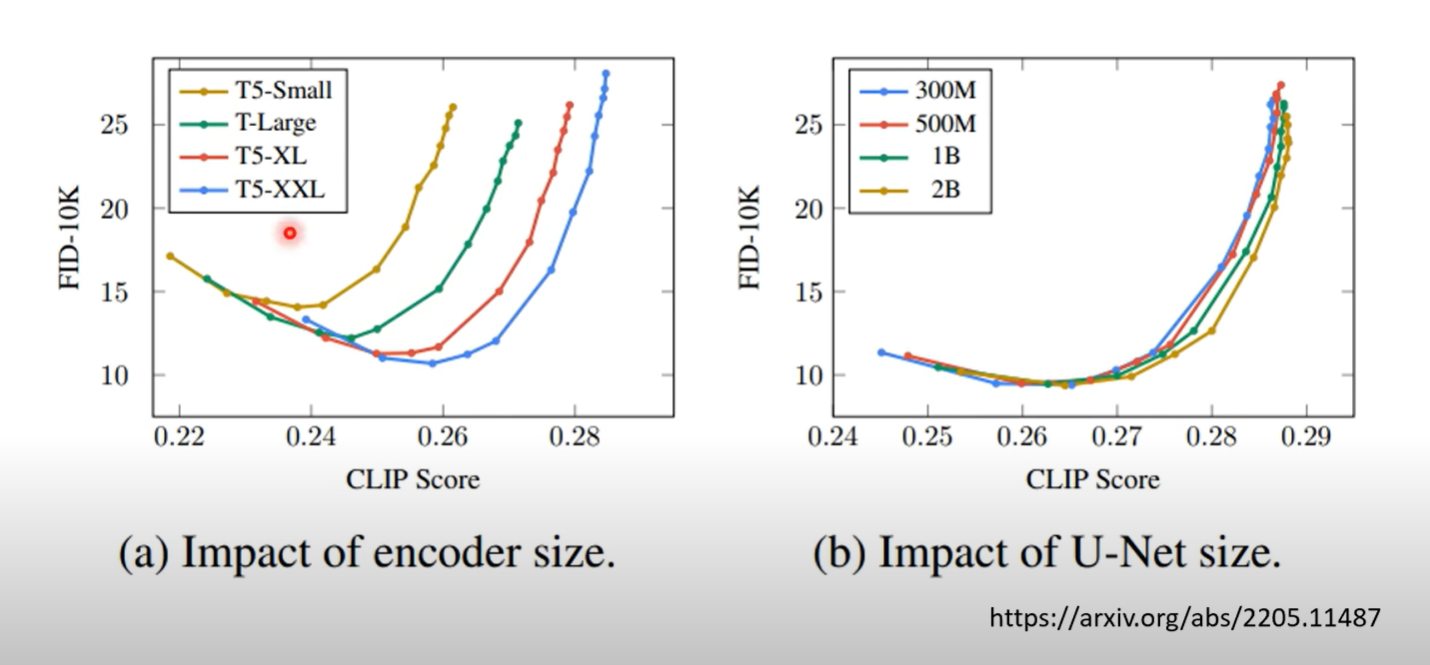
- 文字的encoder会有很大的影响
- FID越低越好
- CLIP分数越高越好
两张图表明,文字的encoder比较重要,越大越好,但是diffusion model影响不大
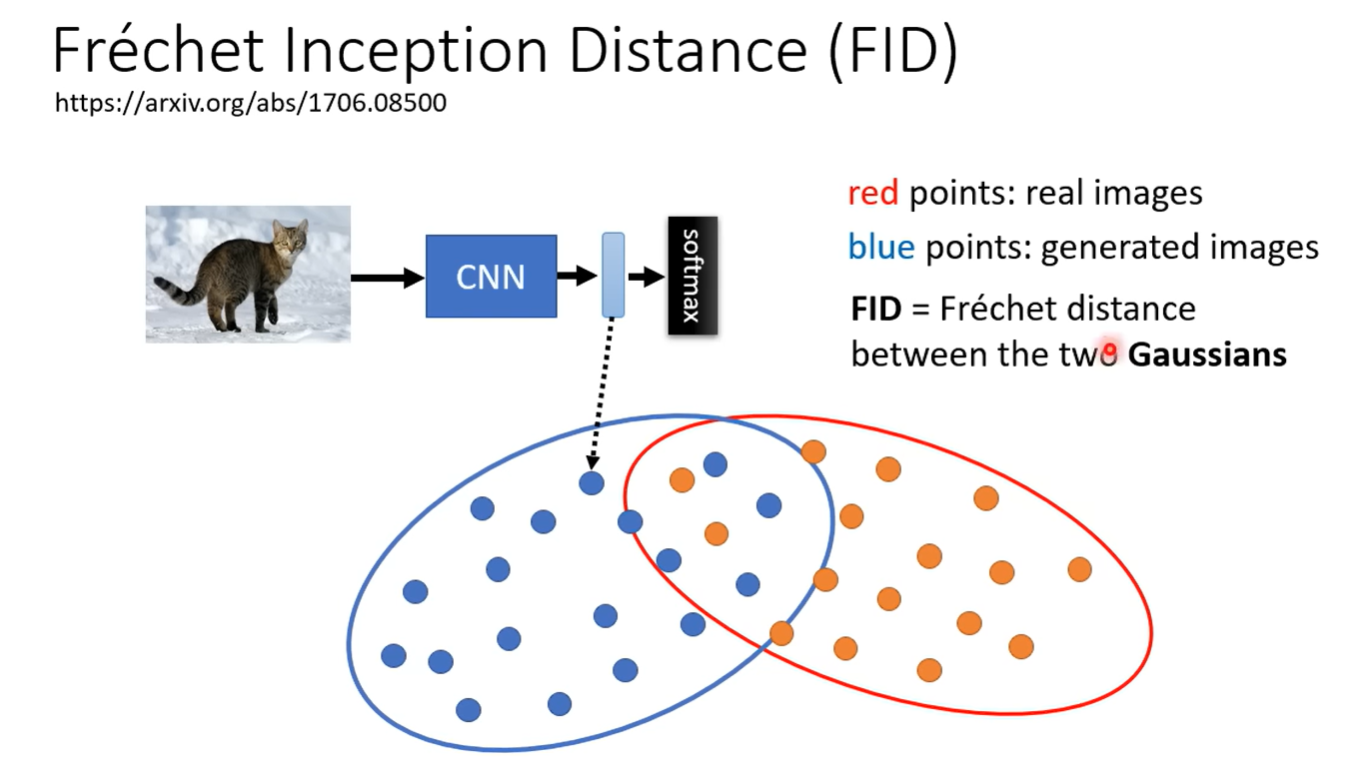
Frechet
FID 一个pre-trained CNN model, 得到CNN的Latent Representation
真实影像的representation和生成的影像的representation
假设两组representation是高斯分布(没什么道理)
计算Frechet distance,距离越小越好
需要比较多的sample来进行计算
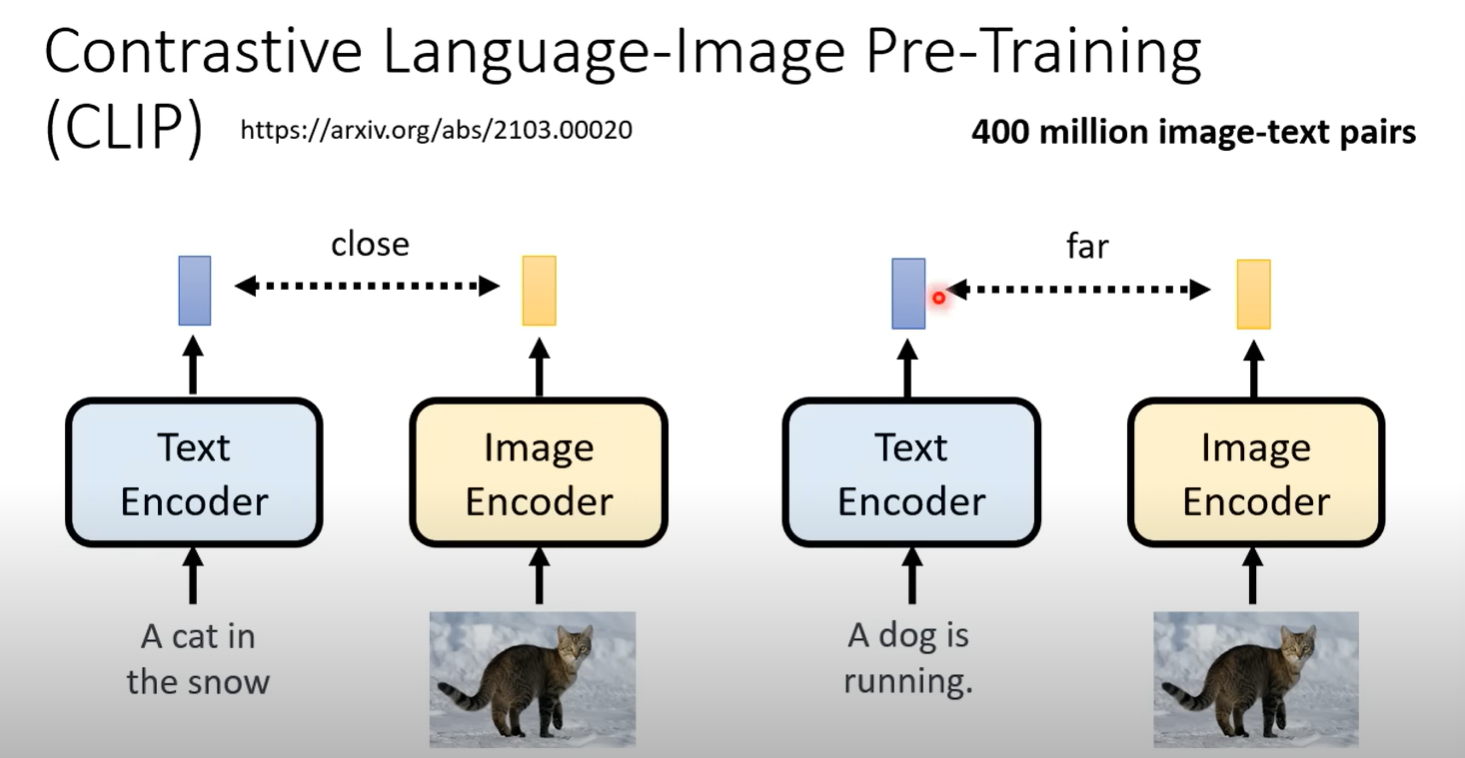
Contrastive
CLIP 400million的image和text对训练得到的模型 将文本(描述)和图片编码,相匹配距离越近越好,不相匹配越远越好
这样的训练认为,CLIP能判断文字和图片的匹配程度---CLIP score
- 将文本和生成的图片输入,看结果是否接近
Decoder
Decoder训练不需要成对的文本和图片
只需要图片的训练就可以获得这种能力
- 如果中间产物是小图
- 将大图缩小,就得到成对的训练数据
- 如果中间产物是latent Representation
- 训练一个Auto-encoder,
- 图片输入,encoder一下变成latent representation,decode一下,变成原图
- 训练完后这个decoder就是对应的decoder
Latent
人类不可读的一张图 如果原图 latent representation 是 都是对应的downsample 是 channel,表示每一个位置是多少个数字来表示 也可以把latent representation 看成图
Generation Model
diffusion model noise加在图片上,杂讯生图
现在diffusion model产生的是中间产物,noise应该加在中间产物(小图片或者latent representation)上
- 怎么得到中间产物
- 用decoder阶段得到的encoder编码一下
- sample 一些noise不断加到中间产物上
获得数据集之后,训练noise predicter
- 文字输入
- step
- 对应的加噪声的图片
Diffusion Model原理剖析
第一讲
VAE & Diffusion
- VAE是将图片经过encoder变成一个latent representation,然后经过decoder恢复成图片
- Diffusion有两个过程,forward process 和 reverse process,forward process可以看成是encode过程
训练算法
伪代码

大概描述
- 重复以下直到converged(收敛)
- 从数据集中sample一张图出来 ← 原图
- 从1到 中sample一个数出来 ← 程度指示(步数)
- 从normal distribution 中sample一个 ← 杂讯
- 大小和原图一致
然后第五行
- 对 和 做一个加权和(weighted sum)
- 权重是事先定好的,对应数字
- 越来越小
- 整个是一张noisy image
- 越大越小, 中 占比越大,代表noise越大
- 代表Noise predictor,将,noisy image传进去
- ,杂讯图减去noise predictor预测的noise
- 也就可以看到,训练的目的就是接近
- 为什么是接近
- 理论上应该是,对特定阶段加入噪音,模型训练来接近这个噪音
- 实践上变成,直接sample一个噪声通过权重加到原图上,然后预测原噪声
- 数学问题
到这里小结一下,DDPM就是理论上,是diffusion process过程不断加噪声,每一次的加的噪声程度逐渐增加,reverse process过程不断去噪,然后实际上通过数学手段,实现变为 指定步数和噪声,按指定的步数权重加噪,然后预测噪声,直接还原图片
生成过程
伪代码

大概描述
- 是从正态分布中sample出来的一个全是杂讯的图
- 遍历T到1, 每次再次从正态分布中sample一个,的时候
- 每次生成下一个图,下标减一
- 直到遍历完
那每次怎么产生下一个图
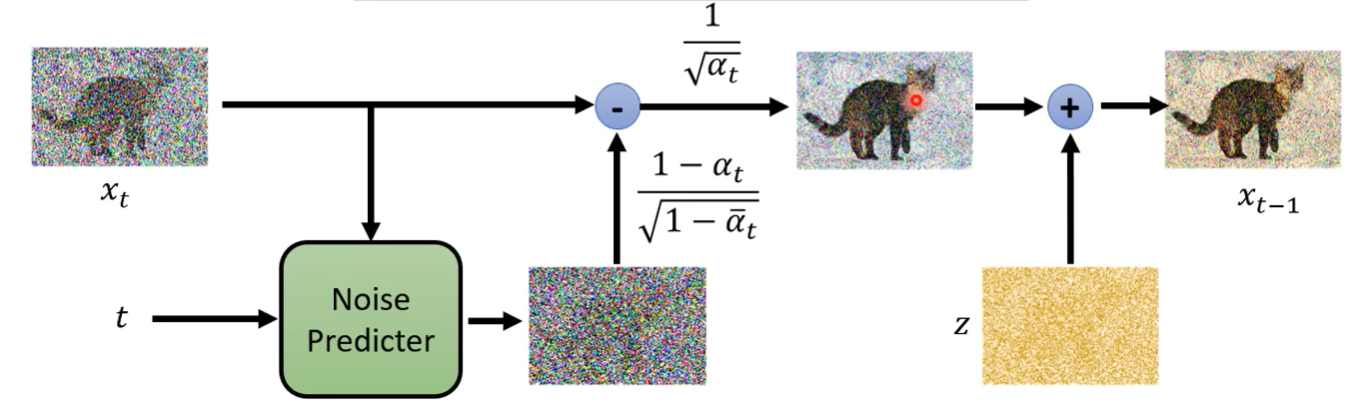
- 上一次迭代的图和t输入到noise predicter 中,noise predicter预测杂讯,然后竟然要乘以一个常数得到需要减去的杂讯,原图减去这个杂讯之后,竟然要再乘以一个常数,然后竟然还要再加上一个系数与sample的杂讯z的乘积才得到最终输出
第二讲
影像生成模型本质上的共同目标
从一个简单的地方生成一张图
在input的地方,有一个简单的distribution(Gaussion Distribution,例如),sample一下,得到一个vector ,丢到一个network中 输出一个,是一张图片
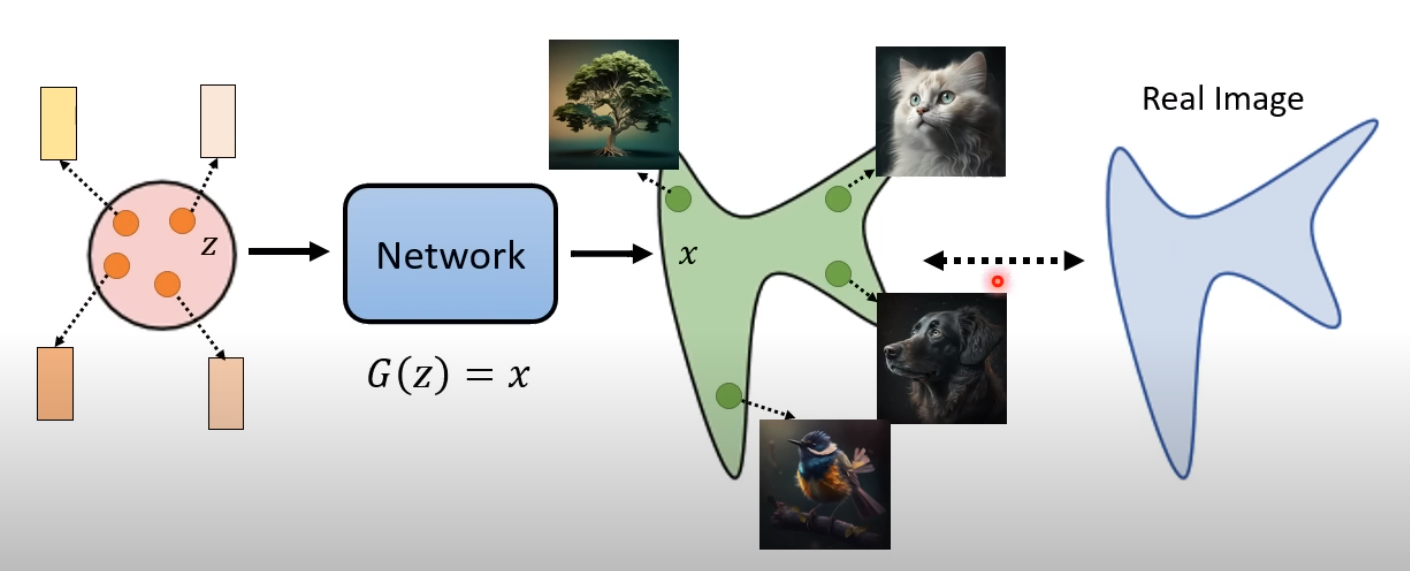
- 在高斯分布的空间里,随意取出一个sample,通过一个network都可以产生一张图
- 有network产生的图所构成的空间/distribution,和现实世界的图的空间/distribution 越接近越好
在文生图之中
- 区别在于加入了对图像的描述(caption),称condition
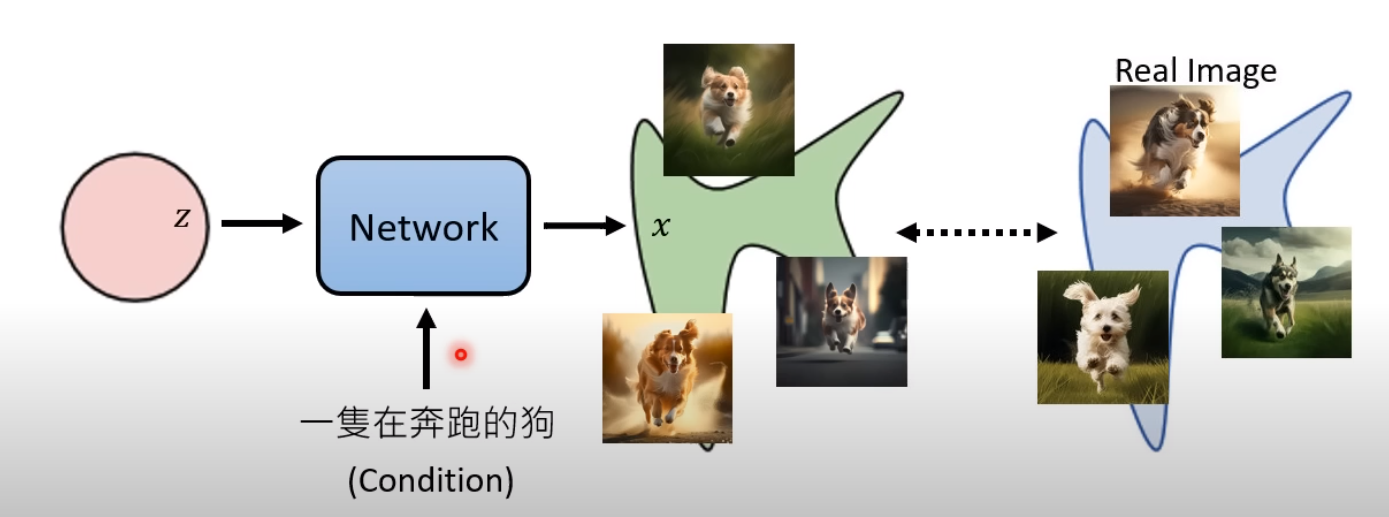
希望network完成一个映射,从简单的distribution,(加上condition),映射到复杂的类似于现实世界的图片distribution中,与现实世界越接近越好
如何才算接近
- Maximum Likelihood Estimation(最大似然估计)
- network ,映射到的distribution ,现实世界的distribution
搜集数据集
假设能够计算 (生成某一张图的几率)
那么objective function 就会是
找到一个使得生成上面sample的图片概率最高的
- 这个就叫maximum likelihood Estimation
- 最大似然估计
- 估计一个参数的取值
- 从样本空间中取样,找到所有可能参数取值下,这些样本发生的事件概率最大的参数
什么道理
进一步的数学推导
- 取log
- 求sample出来的 对应的概率和最大,近似于求整个distribution的期望最大
- 期望的计算
- 也就等价于(减去一个常数)
- 那就是
- 这项就是和的KL divergence(KL 散度)的负值
- 取最大变成取最小
- 那就是说
极大似然等价于使得两个分布之间距离最小
怎么算
类比VAE的话
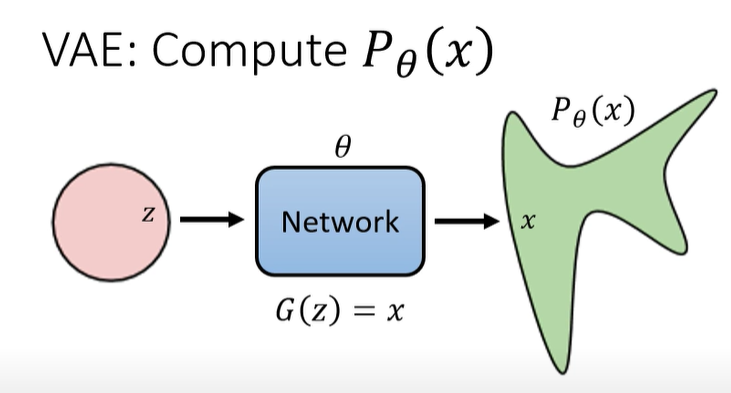
全概率公式
是高斯分布,但是后一项该如何考虑
可以这么定义
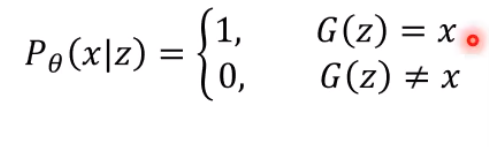
- 但是大概率基本都是0,很难找到 使得
VAE中假设,给定 , 是一个Gaussion Distribution的 Mean
那就有
- 好像是正态分布期望在几何上的性质
- x与期望距离越远,概率在钟形曲线上越小
- 暂时理解为,给定z,模型的输出服从高斯分布, 是给定z模型理想输出即高斯分布的均值,则此时给定z得到x的概率就与 和 x 的距离的相反数成正比
DDPM中,当每一次增加的噪声很小时,可以将 当成是一个高斯分布,我们需要模型预测这个高斯分布,即预测均值和方差。在多数实践中,我们假设模型预测的是分布的均值
则给定 reverse process 每一步降噪的目标 产生的概率和 目标 与均值的距离成反比
有DDPM的 满足(全概率公式)
所有的T的可能情况下, 的加和(积分) 是直接sample出来的,所以和模型参数没有关系
得到这个信息后,我们考虑maximize
由于过于难算,所以一般转变为maximize 的 lowerbound
有如下推导(在Variational Autoencoder(VAE) 中已经见过一次)
引入一个简单的分布,等式成立与分布无关
利用贝叶斯公式写成可拆分的形式,引入一项 用于化简
拆分得到
发现第二项是KL divergence
KL divergence 一定大于0,所以 一定满足
这一项可以转化为一个均值
这个均值就是lowerbound
DPPM 通过类似的推导也能得到一个类似的 lower bound
- 在VAE中是 encoder,而 是一个给定 的Diffusion Process
第三讲
怎么算
服从标准正态分布
则有
所以 服从均值为 ,方差为 的正态分布
根据 和 的关系,可以直接得到指定步数 t 的分布

直接代入,根据正态分布相加得到,详见另一篇笔记 Diffusion
简化一下,令 ,
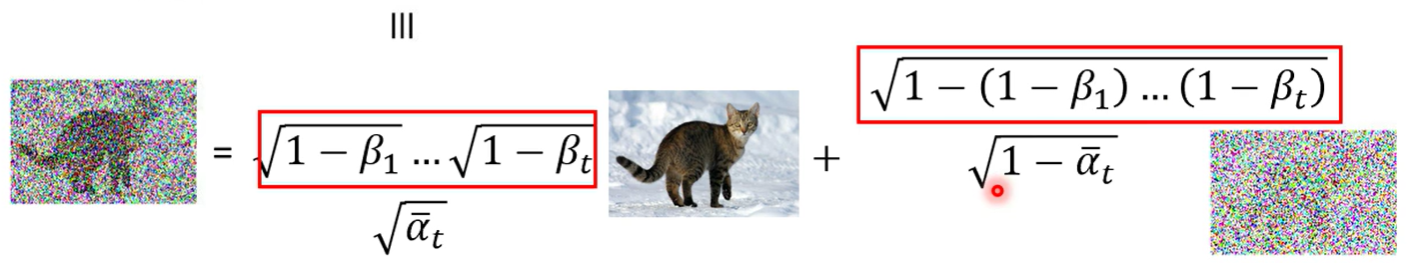
给定步数T和超参数 ,就能直接得到 而不用一步步算
回到 loss function
我们已经得到了 lower bound
我们可以通过一系列推导得到能够计算的表达式
分为三项,第一项和第三项和模型(reverse process)有关,第二项是,diffusion process的过程和从Gaussian sample的概率,和模型参数无关
说第三项和第一项处理方式接近,只展开第三项的求解
这个式子是在 分布上,两个不知道什么分布的KL divergence
分别是 和
怎么计算 ?
结合乘法公式有这么个过程
关于中间的式子, 是怎么来的,我认为是原本应该是 这样后面才有 的展开,但是由于 马尔可夫性质, 与 无关,所以直接写成
计算出来的这个式子又是什么?
经过一番倒推,可以得到这仍然是一个Gaussian distribution
它的 mean 是
variance是
则 分布可知
是已知项(就是模型的预测),也是一个Gaussian distribution
那就可以计算 KL divergence
但我们并不是真的需要这个解析解,我们需要的是minimize KL divergence
现在 的分布已知,mean和variance都与模型无关,其相当于一个固定的分布。 与模型相关,但是我们只关心它的均值(模型的输出)而不关心它的方差
所以最小化 KL divergence的方法就是让二者的均值越接近越好
所以实际上做的就是
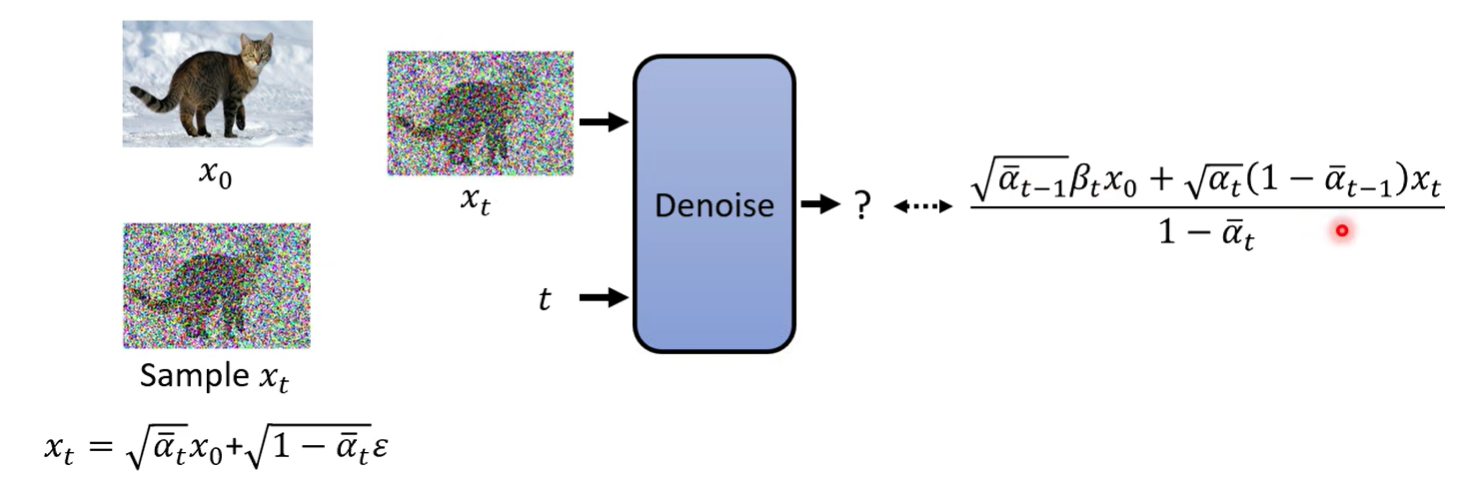
给定 和 ,模型的输出与 的均值越接近越好
对右边的式子代入 表示的 ,得到更简单的式子
式子中只有 是未知的,所以模型需要做的就是预测

回到生成过程的伪代码
这个 就是 模型的输出
小结
实际上的顺序可能是
在diffusion process 和 reverse process 的前提下
我们考虑目标函数: maximize
经过一系列推导,我们发现最终做的相当于使得两个分布 和 模型分布 越接近越好
在假设下,我们不考虑 的方差,则目标变成 最小化 两个均值的距离
经过进一步计算我们得到了
发现其中 模型真正需要预测的只有 ,则损失函数变成,给定t和图像,得到加入的
然后在生成的时候一步步减去noise
第四讲
但是,为什么最后还有一项 呢
模型的输出被假设为一个Gaussian 的mean,所以为了能够描述一个Gaussian,很自然会加上一个 noise 来还原 Gaussian 的分布
但是只取 mean 不是也很合理吗
老师在这里进行了一些猜想
为什么需要sample
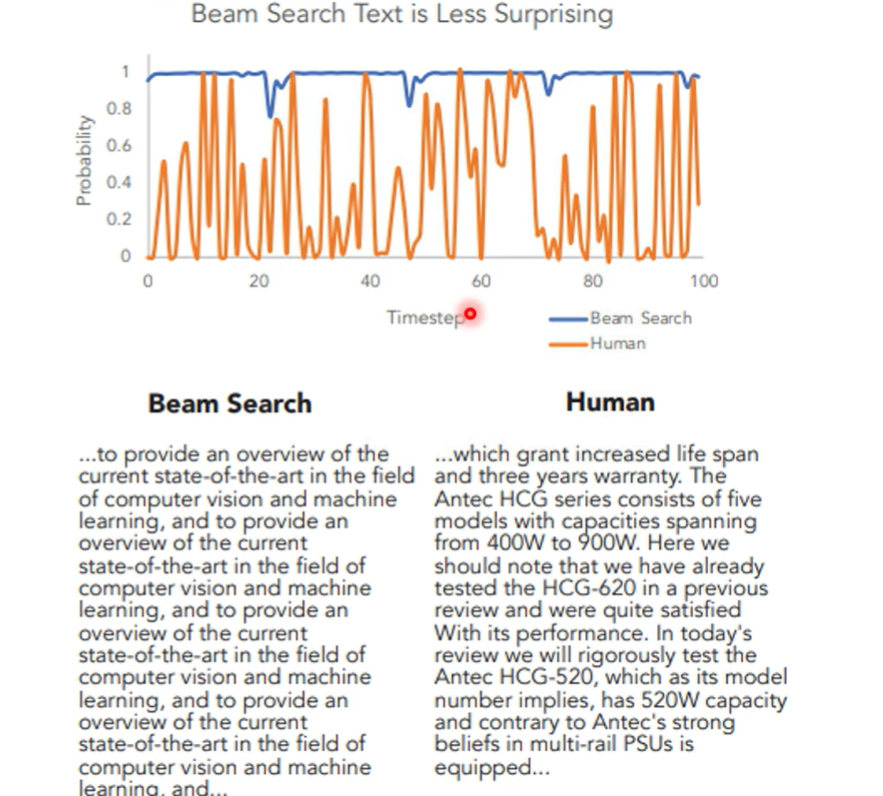
- 有一篇文章在GPT 2上进行了研究,如果只使用概率最大的结果,模型会重复输出相同的话
- 语音合成领域也会在testing的时候加入dropout
所以可能diffusion也是为了避免模型只重复输出概率最大而加入了variance
Application
Diffusion 可以用在语音上
但是用在文字上比较复杂 (文字是discrete的,难以加noise)
- 可以加Gaussian在 word embedding上
- 可以加其它种类的noise
为什么 Diffusion 的结果这么好?
可能的原因是 将autoregressive的方法加上non auto regressive中
将一步解决的问题变成多步解决
有一种 mask-predict 的方法
Nonauto regressive 一次输出如果举棋不定的话,可以将概率小的盖住,再进行一次decode
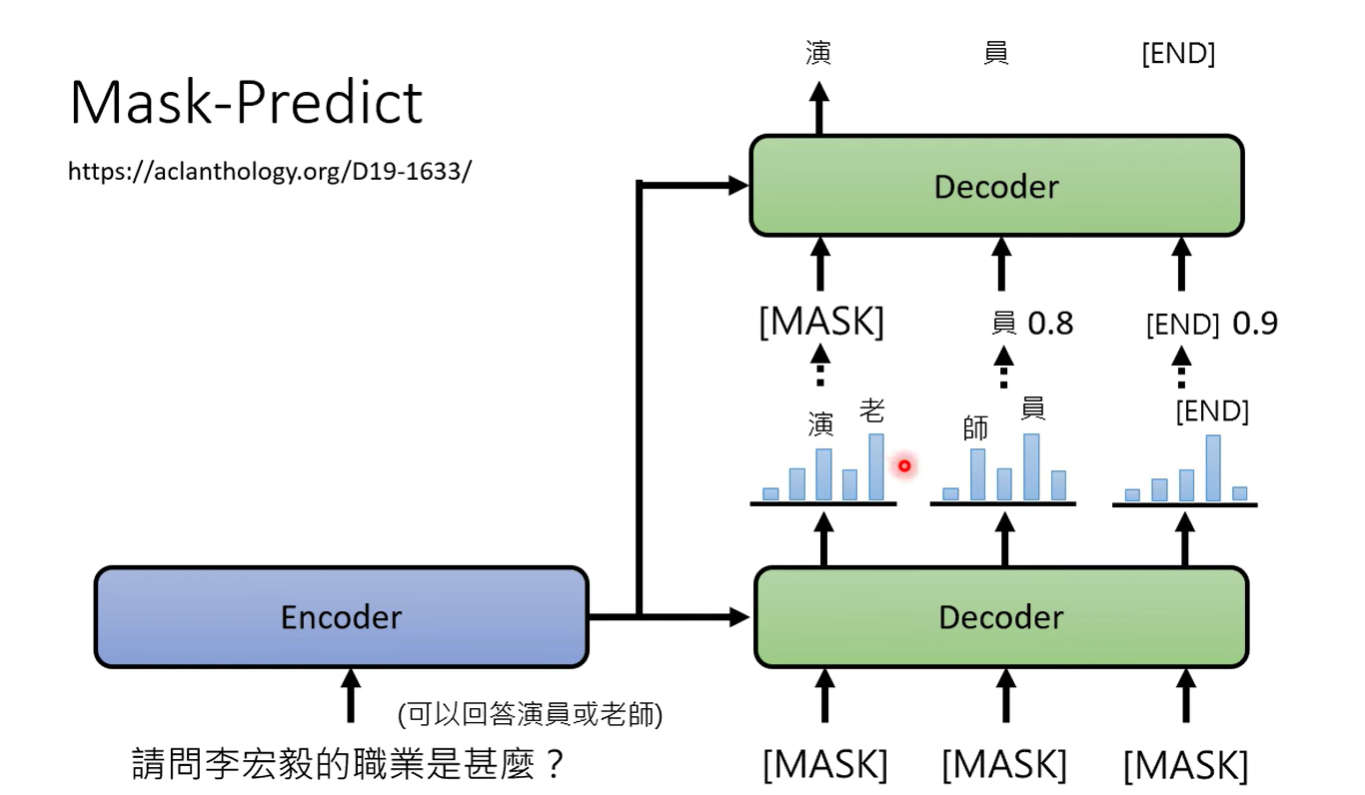
概率大的结果认为是好结果,但是第一次sample的结果可能做得比较糟糕,所以我们再sample一次看看