Residuals vs Fitted
The plot shows if residuals have non-linear patterns
判断是否存在非线性关系,如果残差围绕水平线均匀的分布而且没有显著的特征的话,认为数据不存在非线性关系,模型正确地拟合了数据
实际上,残差图在模型正确拟合的情况下会呈现随机分布,不止适用于线性模型
同时残差的趋势在线性模型下可能能够描述出预测变量与响应变量之间的真实关系(线性函数对真实分布的影响比较小,可能比较直观)
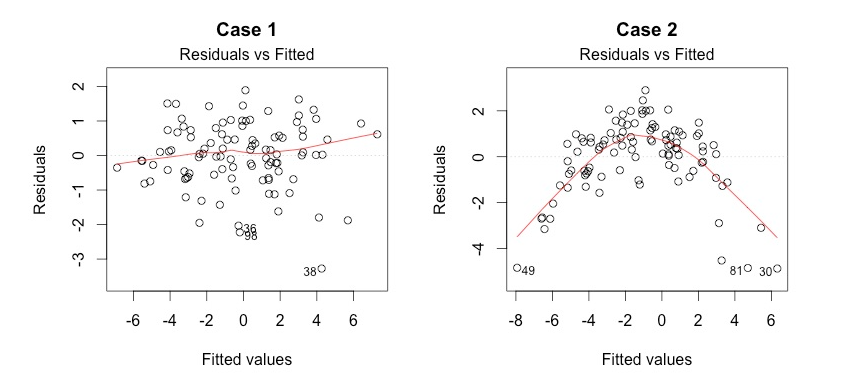
左边是线性模型比较正确的拟合了数据,右边可能存在着二次的关系
Normal Q-Q
This plot shows if residuals are normally distributed
判断残差是否符合正态分布,如果残差沿着直线,认为残差遵循正态分布(线性模型的假设之一)
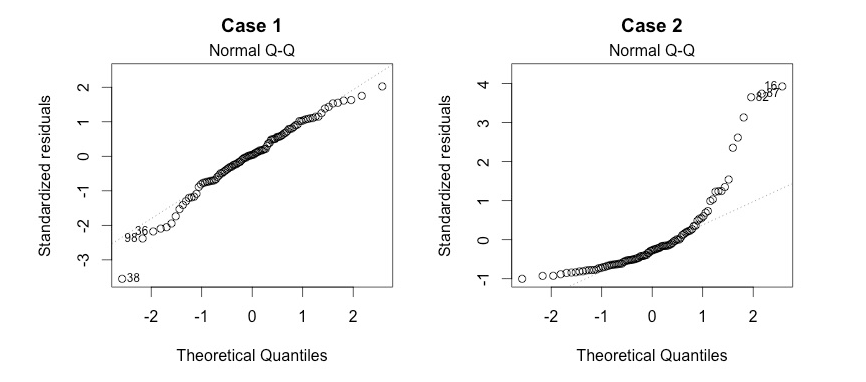
左边的图认为符合正态分布,右边则认为不遵循
Scale-Location
This plot shows if the residuals spread equally along the ranges of predictors(不受预测变量的影响保持同方差)
检验残差是否满足同方差性(homoscedasticity /ˌhəʊ.məʊ.skɪ.dæsˈtɪs.ə.ti/)(线性模型的假设之一),如果红色曲线(残差的平方根)水平,同时残差均匀分布在曲线周围,则认为同方差性被满足
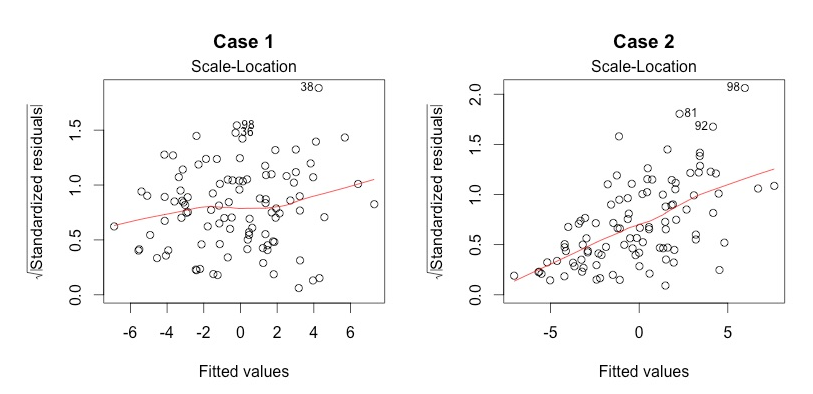
Residuals vs Leverage
This plot shows if there are influential points
用于离群点(outliers)和高杠杆点(leverage points)的检验。
不是所有高杠杆点都会产生负面影响,产生负面影响的点称influential points
如果点位于cook‘s distance虚线外,则认为该点是influential point(一般是高杠杆点和离群点)
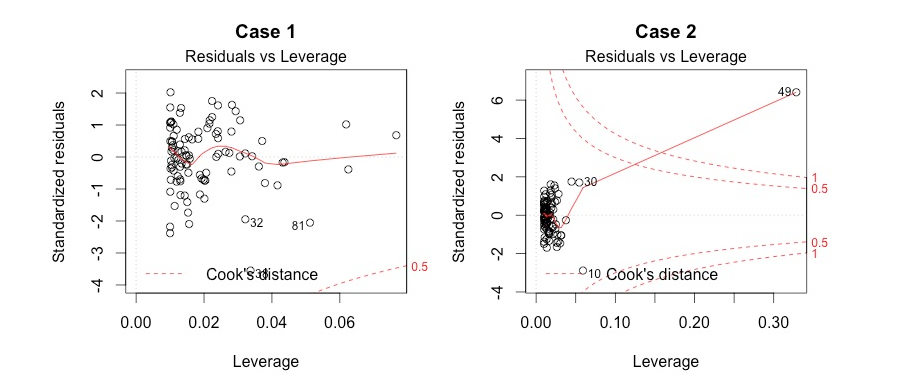
高杠杆点(leverage points)是指具有异常预测变量数值的点(x-value),离群点(outliers)是指拥有异常响应变量的点(y-value)
高杠杆点不一定是离群点,好高杠杆点(good leverage point)会增加模型精度,坏高杠杆点(bad leverage point)影响模型表现
关于高杠杆点
可以通过杠杆值(leverage value)判断是否是高杠杆点
如果leverage 大于 ,其中k为预测变量个数,n为样本点,则认为该点为高杠杆点
关于离群点
通过标准残差判断离群点,如果大于2.5者小于-2.5可以认为是离群点(比较严格),或者是超过3的点认为是离群点